7.1: More on Intervals in Eⁿ. Semirings of Sets
- Page ID
- 19204
I. As a prologue, we turn to intervals in \(E^{n}\) (Chapter 3, §7).
If \(A\) and \(B\) are intervals in \(E^{n},\) then
(i) \(A \cap B\) is an interval (\(\emptyset\) counts as an interval);
(ii) \(A-B\) is the union of finitely many disjoint intervals (but need not be an interval itself).
- Proof
-
The easy proof for \(E^{1}\) is left to the reader.
An interval in \(E^{2}\) is the cross-product of two line intervals.
Let
\[A=X \times Y \text { and } B=X^{\prime} \times Y^{\prime},\]
where \(X, Y, X^{\prime},\) and \(Y^{\prime}\) are intervals in \(E^{1}.\) Then (see Figure 29)
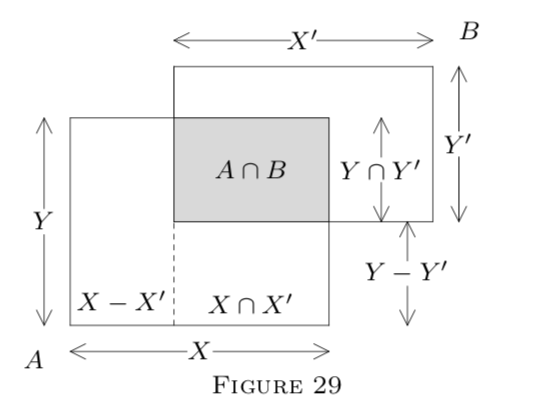
and
\[A-B=\left[\left(X-X^{\prime}\right) \times Y\right] \cup\left[\left(X \cap X^{\prime}\right) \times\left(Y-Y^{\prime}\right)\right];\]
see Problem 8 in Chapter 1, §§1-3.
As the theorem holds in \(E^{1}\),
\[X \cap X^{\prime} \text { and } Y \cap Y^{\prime}\]
are intervals in \(E^{1},\) while
\[X-Y^{\prime} \text { and } Y-Y^{\prime}\]
are finite unions of disjoint line intervals. (In Figure 29 they are just intervals, but in general they are not.)
It easily follows that \(A \cap B\) is an interval in \(E^{2},\) while \(A-B\) splits into finitely many such intervals. (Verify!) Thus the theorem holds in \(E^{2}\).
Finally, for \(E^{n},\) use induction. An interval in \(E^{n}\) is the cross-product of an interval in \(E^{n-1}\) by a line interval. Thus if the theorem holds in \(E^{n-1},\) the same argument shows that it holds in \(E^{n},\) too. (Verify!)
This completes the inductive proof.\(\quad \square\)
Actually, Theorem 1 applies to many other families of sets (not necessarily intervals or sets in \(E^{n}).\) We now give such families a name.
A family \(\mathcal{C}\) of arbitrary sets is called a semiring iff
(i) \(\emptyset \in \mathcal{C}\) (\(\emptyset\) is a member), and
(ii) for any sets \(A\) and \(B\) from \(\mathcal{C},\) we have \(A \cap B \in \mathcal{C},\) while \(A-B\) is the union of finitely many disjoint sets from \(\mathcal{C}.\)
Briefly: \(\mathcal{C}\) is a semiring iff it satisfies Theorem 1.
Note that here \(\mathcal{C}\) is not just a set, but a whole family of sets. Recall (Chapter §§1-3) that a set family (family of sets) is a set \(\mathcal{M}\) whose members are other sets. If \(A\) is a member of \(\mathcal{M},\) we call \(A\) an \(\mathcal{M}\)-set and write \(A \in \mathcal{M}\) (not \(A \subseteq \mathcal{M})\).
Sometimes we use index notation:
\[\mathcal{M}=\left\{X_{i} | i \in I\right\},\]
briefly
\[\mathcal{M}=\left\{X_{i}\right\},\]
where the \(X_{i}\) are \(\mathcal{M}\)-sets distinguished from each other by the subscripts \(i\) varying over some index set \(I.\)
A set family \(\mathcal{M}=\left\{X_{i}\right\}\) and its union
\[\bigcup_{i} X_{i}\]
are said to be disjoint iff
\[X_{i} \cap X_{j}=\emptyset \text { whenever } i \neq j.\]
Notation:
\[\bigcup X_{i} \text{ (disjoint).}\]
In our case, \(A \in \mathcal{C}\) means that \(A\) is a \(\mathcal{C}\)-set (a member of the semiring \(\mathcal{C})\).
The formula
\[(\forall A, B \in \mathcal{C}) \quad A \cap B \in \mathcal{C}\]
means that the intersection of two \(\mathcal{C}\)-sets in a \(\mathcal{C}\)-set itself.
Henceforth, we will often speak of semirings \(\mathcal{C}\) in general. In particular, this will apply to the case \(\mathcal{C}=\){intervals}. Always keep this case in mind!
Note 1. By Theorem 1, the intervals in \(E^{n}\) form a semiring. So also do the half-open and the half-closed intervals separately (same proof!), but not the open (or closed) ones. (Why?)
Caution. The union and difference of two \(\mathcal{C}\)-sets need not be a \(\mathcal{C}\)-set. To remedy this, we now enlarge \(\mathcal{C}.\)
We say that a set \(A\) (from \(\mathcal{C}\) or not) is \(\mathcal{C}\)-simple and write
\[A \in \mathcal{C}_{s}^{\prime}\]
iff \(A\) is a finite union of disjoint \(\mathcal{C}\)-sets (such as \(A-B\) in Theorem 1).
Thus \(\mathcal{C}_{s}^{\prime}\) is the family of all \(\mathcal{C}\)-simple sets.
Every \(\mathcal{C}\)-set is also a \(\mathcal{C}_{s}^{\prime}\)-set, i.e., a \(\mathcal{C}\)-simple one. (Why?) Briefly:
\[\mathcal{C} \subseteq \mathcal{C}_{s}^{\prime}.\]
If \(\mathcal{C}\) is the set of all intervals, a \(\mathcal{C}\)-simple set may look as in Figure 30.
If \(\mathcal{C}\) is a semiring, and if \(A\) and \(B\) are \(\mathcal{C}\)-simple, so also are
\[A \cap B, A-B, \text { and } A \cup B.\]
In symbols,
\[\left(\forall A, B \in \mathcal{C}_{s}^{\prime}\right) \quad A \cap B \in \mathcal{C}_{s}^{\prime}, A-B \in \mathcal{C}_{s}^{\prime}, \text { and } A \cup B \in \mathcal{C}_{s}^{\prime}.\]
- Proof
-
We give a proof outline and suggest the proof as an exercise. Before attempting it, the reader should thoroughly review the laws and problems of Chapter 1, §§1-3.
(1) To prove \(A \cap B \in \mathcal{C}_{s}^{\prime},\) let
\[A=\bigcup_{i=1}^{m} A_{i}(\text {disjoint}) \text { and } B=\bigcup_{k=1}^{n} B_{k} \text { (disjoint),}\]
with \(A_{i}, B_{k} \in \mathcal{C}.\) Verify that
\[A \cap B=\bigcup_{k=1}^{n} \bigcup_{i=1}^{m}\left(A_{i} \cap B_{k}\right) \text { (disjoint),}\]
and so \(A \cap B \in \mathcal{C}_{s}^{\prime}\).
(2) Next prove that \(A-B \in \mathcal{C}_{s}^{\prime}\) if \(A \in \mathcal{C}_{s}^{\prime}\) and \(B \in \mathcal{C}\).
Indeed, if
\[A=\bigcup_{i=1}^{m} A_{i} \text { (disjoint),}\]
then
\[A-B=\bigcup_{i=1}^{m} A_{i}-B=\bigcup_{i=1}^{m}\left(A_{i}-B\right) \text { (disjoint).}\]
Verify and use Definition 2.
(3) Prove that
\[\left(\forall A, B \in \mathcal{C}_{s}^{\prime}\right) \quad A-B \in \mathcal{C}_{s}^{\prime};\]
we suggest the following argument.
Let
\[B=\bigcup_{k=1}^{n} B_{k}, \quad B_{k} \in \mathcal{C}.\]
Then
\[A-B=A-\bigcup_{k=1}^{n} B_{k}=\bigcap_{k=1}^{n}\left(A-B_{k}\right)\]
by duality laws. But \(A-B_{k}\) is \(\mathcal{C}\)-simple by step (2). Hence so is
\[A-B=\bigcap_{k=1}^{m}\left(A-B_{k}\right)\]
by step (1) plus induction.
(4) To prove \(A \cup B \in \mathcal{C}_{s}^{\prime},\) verify that
\[A \cup B=A \cup(B-A),\]
where \(B-A \in \mathcal{C}_{s}^{\prime},\) by (3).
Note 2. By induction, Theorem 2 extends to any finite number of \(\mathcal{C}_{s}^{\prime}\)-sets. It is a kind of "closure law."
We thus briefly say that \(\mathcal{C}_{s}^{\prime}\) is closed under finite unions, intersections, and set differences. Any (nonempty) set family with these properties is called a set ring (see also §3).
Thus Theorem 2 states that if \(\mathcal{C}\) is a semiring, then \(\mathcal{C}_{s}^{\prime}\) is a ring.
Caution. An infinite union of \(\mathcal{C}\)-simple sets need not be \(\mathcal{C}\)-simple. Yet we may consider such unions, as we do next.
In Corollary 1 below, \(\mathcal{C}_{s}^{\prime}\) may be replaced by any set ring \(\mathcal{M}\).
If \(\left\{A_{n}\right\}\) is a finite or infinite sequence of sets from a semiring \(\mathcal{C}\) (or from a ring \(\mathcal{M}\) such as \(\mathcal{C}_{s}^{\prime}\)), then there is a disjoint sequence of \(\mathcal{C}\)-simple sets (or \(\mathcal{M}\)-sets) \(B_{n} \subseteq A_{n}\) such that
\[\bigcup_{n} A_{n}=\bigcup_{n} B_{n}.\]
- Proof
-
Let \(B_{1}=A_{1}\) and for \(n=1,2, \ldots\),
\[B_{n+1}=A_{n+1}-\bigcup_{k=1}^{n} A_{k}, \quad A_{k} \in \mathcal{C}.\]
By Theorem 2, the \(B_{n}\) are \(\mathcal{C}\)-simple (as are \(A_{n+1}\) and \(\bigcup_{k=1}^{n} A_{k}).\) Show that they are disjoint (assume the opposite and find a contradiction) and verify that \(\bigcup A_{n}=\bigcup B_{n}:\) If \(x \in \bigcup A_{n},\) take the least \(n\) for which \(x \in A_{n}.\) Then \(n>1\) and
\[x \in A_{n}-\bigcup_{k=1}^{n-1} A_{k}=B_{n},\]
or \(n=1\) and \(x \in A_{1}=B_{1}. \quad \square\)
Note 3. In Corollary 1, \(B_{n} \in \mathcal{C}_{s}^{\prime},\) i.e., \(B_{n}=\bigcup_{i=1}^{m_{n}} C_{n i}\) for some disjoint sets \(C_{n i} \in \mathcal{C}.\) Thus
\[\bigcup_{n} A_{n}=\bigcup_{n} \bigcup_{i=1}^{m_{n}} C_{n i}\]
is also a countable disjoint union of \(\mathcal{C}\)-sets.
II. Recall that the volume of intervals is additive (Problem 9 in Chapter 3, §7). That is, if \(A \in \mathcal{C}\) is split into finitely many disjoint subintervals, then \(v A\) (the volume of \(A)\) equals the sum of the volumes of the parts.
We shall need the following lemma.
Let \(X_{1}, X_{2}, \ldots, X_{m} \in \mathcal{C}\) (intervals in \(E^{n}).\) If the \(X_{i}\) are mutually disjoint, then
(i) \(\bigcup_{i=1}^{m} X_{i} \subseteq Y \in \mathcal{C}\) implies \(\sum_{i=1}^{m} v X_{i} \leq v Y;\) and
(ii) \(\bigcup_{i=1}^{m} X_{i} \subseteq \bigcup_{k=1}^{p} Y_{k}\left(\text {with } Y_{k} \in \mathcal{C}\right)\) implies \(\sum_{i=1}^{m} v X_{i} \leq \sum_{k=1}^{p} v Y_{k}\).
- Proof
-
(i) By Theorem 2, the set
\[Y-\bigcup_{i=1}^{m} X_{i}\]
is \(\mathcal{C}\)-simple; so
\[Y-\bigcup_{i=1}^{m} X_{i}=\bigcup_{j=1}^{q} C_{j}\]
for some disjoint intervals \(C_{j}.\) Hence
\[Y=\bigcup X_{i} \cup \bigcup C_{j} \text { (all disjoint).}\]
Thus by additivity,
\[v Y=\sum_{i=1}^{m} v X_{i}+\sum_{j=1}^{q} v C_{j} \geq \sum_{i=1}^{m} v X_{i},\]
as claimed.
(ii) By set theory (Problem 9 in Chapter 1, §§1-3),
\[X_{i} \subseteq \bigcup_{k=1}^{p} Y_{k}\]
implies
\[X_{i}=X_{i} \cap \bigcup_{k=1}^{p} Y_{k}=\bigcup_{k=1}^{p}\left(X_{i} \cap Y_{k}\right).\]
If it happens that the \(Y_{k}\) are mutually disjoint also, so certainly are the smaller intervals \(X_{i} \cap Y_{k};\) so by additivity,
\[v X_{i}=\sum_{k=1}^{p} v\left(X_{i} \cap Y_{k}\right).\]
Hence
\[\sum_{i=1}^{m} v X_{i}=\sum_{i=1}^{m} \sum_{k=1}^{p} v\left(X_{i} \cap Y_{k}\right)=\sum_{k=1}^{p}\left[\sum_{i=1}^{m} v\left(X_{i} \cap Y_{k}\right)\right].\]
But by (i),
\[\sum_{i=1}^{m} v\left(X_{i} \cap Y_{k}\right) \leq v Y_{k} \text { (why?);}\]
so
\[\sum_{i=1}^{m} v X_{i} \leq \sum_{k=1}^{p} v Y_{k},\]
as required.
If, however, the \(Y_{k}\) are not disjoint, Corollary 1 yields
\[\bigcup Y_{k}=\bigcup B_{k} \text { (disjoint)},\]
with
\[Y_{k} \supseteq B_{k}=\bigcup_{j=1}^{m_{k}} C_{k j}(\text {disjoint}), \quad C_{k j} \in \mathcal{C}.\]
By (i),
\[\sum_{j=1}^{m_{k}} v C_{k j} \leq v Y_{k}.\]
As
\[\bigcup_{i=1}^{m} X_{i} \subseteq \bigcup_{k=1}^{p} Y_{k}=\bigcup_{k=1}^{p} B_{k}=\bigcup_{k=1}^{p} \bigcup_{j=1}^{m_{k}} C_{k j} \text { (disjoint),}\]
all reduces to the previous disjoint case.\(\quad \square\)
Let \(A \in \mathcal{C}_{s}^{\prime}\) (\(\mathcal{C}=\) intervals in \(E^{n}\)). If
\[A=\bigcup_{i=1}^{m} X_{i}(\text {disjoint})=\bigcup_{k=1}^{p} Y_{k} \text { (disjoint)}\]
with \(X_{i}, Y_{k} \in \mathcal{C},\) then
\[\sum_{i=1}^{m} v X_{i}=\sum_{k=1}^{p} v Y_{k}.\]
(Use part (ii) of the lemma twice.)
Thus we can (and do) unambiguously define \(v A\) to be either of these sums.


