2.4: Upper and Lower Bounds. Completeness
- Page ID
- 19031
A subset \(A\) of an ordered field \(F\) is said to be bounded below (or left bounded) iff there is \(p \in F\) such that
\[(\forall x \in A) \quad p \leq x\]
\(A\) is bounded above (or right bounded) iff there is \(q \in F\) such that
\[(\forall x \in A) \quad x \leq q\]
In this case, \(p\) and \(q\) are called, respectively, a lower (or left) bound and an upper (or right) bound, of \(A .\) If both exist, we simply say that \(A\) is bounded (by \(p\) and \(q ) .\) The empty set \(\emptyset\) is regarded as ("vacuously") bounded by any p and \(q\) (cf. the end of Chapter \(1, §3 )\).
The bounds \(p\) and \(q\) may, but need not, belong to \(A .\) If a left bound \(p\) is itself in \(A,\) we call it the least element or minimum of \(A,\) denoted min \(A\). Similarly, if \(A\) contains an upper bound \(q,\) we write \(q=\max A\) and call \(q\) the largest element or maximum of \(A .\) However, \(A\) may well have no minimum or
maximum.
Note 1. A finite set \(A \neq \emptyset\) always has a minimum and a maximum (see Problem 9 of §§ 5-6 )\).
Note 2. A set \(A\) can have at most one maximum and at most one minimum. For if it had \(t w o\) maxima \(q, q^{\prime},\) then
\[q \leq q^{\prime}\]
(since \(q \in A\) and \(q^{\prime}\) is a right bound); similarly
\[q^{\prime} \leq q;\]
so \(q=q^{\prime}\) after all. Uniqueness of \(\min A\) is proved in the same manner.
Note 3. If \(A\) has one lower bound \(p,\) it has many (e.g., take any \(p^{\prime}<p )\).
Similarly, if \(A\) has one upper bound \(q,\) it has many (take any \(q^{\prime}>q )\).
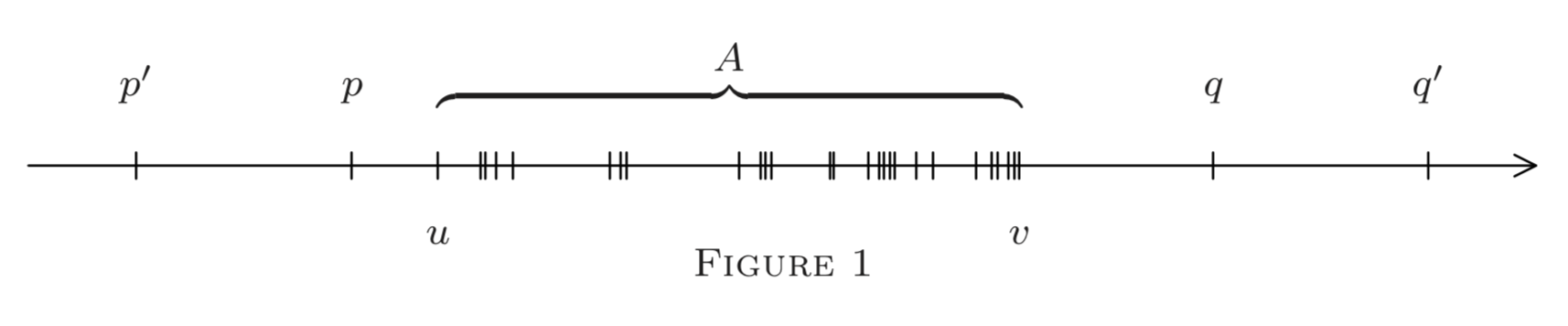
Geometrically, on the real axis, all lower (upper) bounds lie to the left (right) of \(A ;\) see Figure \(1 .\)
(1) Let
\[A=\{1,-2,7\}.\]
Then \(A\) is bounded above \((\) e.g. \(,\) by \(7,8,10, \dots)\) and below \((\) e.g. \(,\) by \(-2,-5,-12, \dots )\).
We have \(\min A=-2, \max A=7\).
(2) The set \(N\) of all naturals is bounded below (e.g., by \(1,0, \frac{1}{2},-1, \ldots\)) and \(1=\min N;\) N has no maximum, for each \(q \in N\) is exceeded by some \(n \in N\) (e.g. \(, n=q+1\)).
(3) Given \(a, b \in F(a \leq b),\) we define in \(F\) the open interval
\[(a, b)=\{x | a<x<b\};\]
the closed interval
\[[a, b]=\{x | a \leq x \leq b\};\]
the half-open interval
\[(a, b]=\{x | a<x \leq b\};\]
and the half-closed interval
\[[a, b)=\{x | a \leq x<b\}.\]
Clearly, each of these intervals is bounded by the endpoints a and \(b ;\) moreover, \(a \in[a, b]\) and \(a \in[a, b)\) (the latter provided \([a, b) \neq \emptyset,\) i.e., \(a<\) \(b ),\) and \(a=\min [a, b]=\min [a, b) ;\) similarly, \(b=\max [a, b]=\max (a, b]\). But \([a, b)\) has no maximum, \((a, b]\) has no minimum, and \((a, b)\) has neither. (Why?)
Geometrically, it seems plausible that among all left and right bounds of \(A\) (if any) there are some "closest" to \(A,\) such as \(u\) and \(v\) in Figure \(1,\) i.e., a least upper bound \(v\) and a greatest lower bound \(u .\) These are abbreviated
\[\operatorname{lub} A \text{ and } \mathrm{glb} A\]
and are also called the supremum and infimum of \(A,\) respectively; briefly,
\[v=\sup A, u=\inf A\]
However, this assertion, though valid in \(E^{1},\) fails to materialize in many other fields such as the field \(R\) of all rationals (cf. \( §§11-12 ) .\) Even for \(E^{1},\) it cannot be proved from Axioms 1 through 9.
On the other hand, this property is of utmost importance for mathematical analysis; so we introduce it as an axiom (for \(E^{1} ),\) called the completeness axiom. It is convenient first to give a general definition.
An ordered field \(F\) is said to be complete iff every nonvoid right-bounded subset \(A \subset F\) has a supremum \((\) i.e., a lub) in \(F\).
Note that we use the term "complete" only for ordered fields.
With this definition, we can give the tenth and final axiom for \(E^{1}\).
The Completeness Axiom
The real field \(E^{1}\) is complete in the above sense. That is, each right-bounded set \(A \subset E^{1}\) has a supremum \((\operatorname{sup} A ) \text { in } E ^ { 1 }\), provided \(A \neq \emptyset\).
The corresponding assertion for infima can now be proved as a theorem.
In a complete field \(F\) ( such as \(E^{1}\)), every nonvoid left-bounded subset \(A \subset F\) has an infimum \((i . e .,\)a glb\()\).
- Proof
-
Let \(B\) be the (nonvoid) set of all lower bounds of \(A\) (such bounds exist since \(A\) is left bounded \() .\) Then, clearly, no member of \(B\) exceeds any member of \(A,\) and so \(B\) is right bounded by an element of \(A .\) Hence, by the assumed completeness of \(F, B\) has a supremum in \(F,\) call it \(p .\)
We shall show that \(p\) is also the required infimum of \(A,\) thus completing the proof.
Indeed, we have
(i) \(p\) is a lower bound of \(A .\) For, by definition, \(p\) is the least upper bound of \(B .\) But, as shown above, each \(x \in A\) is an upper bound of \(B .\) Thus
\[(\forall x \in A) \quad p \leq x\]
(ii) \(p\) is the greatest lower bound of \(A .\) For \(p=\sup B\) is not exceeded by any member of \(B .\) But, by definition, \(B\) contains all lower bounds of \(A ;\) so \(p\) is not exceeded by any of them, i.e.,
\[p=\mathrm{g} 1 \mathrm{b} A=\mathrm{inf} A\]
Note 4. The lub and glb of \(A\) (if they exist) are unique. For inf \(A\) is, by definition, the maximum of the set \(B\) of all lower bounds of \(A,\) and hence unique, by Note \(2 ;\) similarly for the uniqueness of sup \(A .\)
Note 5. Unlike min \(A\) and max \(A,\) the glb and lub of \(A\) need not belong to A. For example, if \(A\) is the interval \((a, b)\) in \(E^{1}(a<b)\) then, as is easily seen,
\[a=\inf A \text{ and } b=\sup A\]
though \(a, b \notin A .\) Thus sup \(A\) and inf \(A\) may exist, though max \(A\) and min \(A\) do not.
On the other hand, if
\[q=\max A(p=\min A)\]
then also
\[q=\sup A(p=\inf A) . \quad(\mathrm{Why} ?)\]
In an ordered field \(F,\) we have \(q=\sup A(A \subset F)\) iff
(i) \((\forall x \in A) \quad x \leq q\) and
(ii) each field element \(p<q\) is exceeded by some \(x \in A ;\) i.e.,
\[(\forall p<q)(\exists x \in A) \quad p<x.\]
Equivalently,
(ii') \[(\forall \varepsilon>0)(\exists x \in A) \quad q-\varepsilon<x ; \quad(\varepsilon \in F)\]
Similarly, \(p=\inf A\) iff
\[(\forall x \in A) \quad p \leq x \quad \text{ and } \quad(\forall \varepsilon>0)(\exists x \in A) \quad p+\varepsilon>x.\]
- Proof
-
Condition (i) states that \(q\) is an upper bound of \(A,\) while (ii) implies that no smaller element \(p\) is such a bound (since it is exceeded by some \(x\) in A). When combined, (i) and (ii) state that \(q\) is the least upper bound.
Moreover, any element \(p<q\) can be written as \(q-\varepsilon(\varepsilon>0) .\) Hence (ii) can be rephrased as \(\left(\mathrm{ii}^{\prime}\right) .\)
The proof for inf \(A\) is quite analogous. \(\square\)
Let \(b \in F\) and \(A \subset F\) in an ordered field \(F .\) If each element \(x\) of \(A\) satisfies \(x \leq b(x \geq b),\) so does sup \(A\), respectively), provided it exists in \(F .\)
In fact, the condition
\[(\forall x \in A) \quad x \leq b\]
means that \(b\) is a right bound of \(A .\) However, sup \(A\) is the least right bound, so sup \(A \leq b ;\) similarly for inf \(A .\)
In any ordered field, \(\emptyset \neq A \subseteq B\) implies
\[\sup A \leq \sup B \text{ and } \inf A \geq \inf B\]
as well as
\[inf A \leq \sup A\]
provided the suprema and infima involved exist.
- Proof
-
Let \(p=\inf B\) and \(q=\sup B\).
As \(q\) is a right bound of \(B\),
\[x \leq q \text{ for all } x \in B.\]
But \(A \subseteq B,\) so \(B\) contains all elements of \(A .\) Thus
\[x \in A \Rightarrow x \in B \Rightarrow x \leq q\]
so, by Corollary \(1,\) also
\[\sup A \leq q=\sup B,\]
as claimed.
Similarly, one gets inf \(A \geq \inf B\).
Finally, if \(A \neq \emptyset,\) we can fix some \(x \in A .\) Then
\[\inf A \leq x \leq \sup A\]
and all is proved. \(\square\)


