5.5: Amazing consequence of Cauchy’s integral formula
- Page ID
- 6499
Existence of derivatives
Suppose \(f(z)\) is analytic on a region \(A\). Then, \(f\) has derivatives of all order.
- Proof
-
This follows from Cauchy’s integral formula for derivatives. That is, we have a formula for all the derivatives, so in particular the derivatives all exist.
A little more precisely: for any point \(z\) in \(A\) we can put a small disk around \(z_0\) that is entirely contained in \(A\). Let \(C\) be the boundary of the disk, then Cauchy’s formula gives a formula for all the derivatives \(f^{(n)} (z_0)\) in terms of integrals over \(C\). In particular, those derivatives exist.
Remark. If you look at the proof of Cauchy’s formula for derivatives you’ll see that \(f\) having derivatives of all orders boils down to \(1/(w - z)\) having derivatives of all orders for \(w\) on a curve not containing \(z\).
Important remark. We have at times assumed that for \(f(u + iv)\) analytic, \(u\) and \(v\) have continuous higher order partial derivatives. This theorem confirms that fact. In particular, \(u_{xy} = u_{yx}\), etc.
Cauchy’s inequality
Let \(C_R\) be the circle \(|z - z_0| = R\). Assume that \(f(z)\) is analytic on \(C_R\) and its interior, i.e. on the disk \(|z - z_0| \le R\). Finally let \(M_R = \text{max } |f(z)|\) over \(z\) on \(C_R\). Then
\[|f^{(n)} (z_0)| \le \dfrac{n! M_R}{R^n}, \ \ \ n = 1, 2, 3, ... \nonumber \]
- Proof
-
Using Cauchy’s integral formula for derivatives (Equation 5.3.1) we have
\[|f^{(n)} (z_0)| \le \dfrac{n!}{2\pi} \int_{C_R} \dfrac{|f(w)|}{|w - z_0|^{n + 1}} |dw| \le \dfrac{n!}{2\pi} \dfrac{M_R}{R^{n + 1}} \int_{C_R} |dw| = \dfrac{n!}{2\pi} \dfrac{M_R}{R^{n + 1}} \int_{C_R} \cdot 2\pi R \nonumber \]
Liouville’s theorem
Assume \(f(z)\) is entire and suppose it is bounded in the complex plane, namely \(|f(z)| < M\) for all \(z \in C\) then \(f(z)\) is constant.
- Proof
-
For any circle of radius \(R\) around \(z_0\) the Cauchy inequality says \(|f'(z_0)| \le \dfrac{M}{R}\). But, \(R\) can be as large as we like so we conclude that \(|f'(z_0)| = 0\) for every \(z_0 \in C\). Since the derivative is 0, the function itself is constant.
In short:
If \(f\) is entire and bounded then \(f\) is constant.
\(P(z) = a_n z^n + ... + a_0\), \(\sin (z)\), \(e^z\) are all entire but not bounded.
Any polynomial \(P\) of degree \(n \ge 1\), i.e.
\[P(z) = a_0 + a_1 z + ... + a_n z^n, a_n \ne 0, \nonumber \]
has exactly \(n\) roots.
- Proof
-
There are two parts to the proof.
Hard part: Show that \(P\) has at least one root.
This is done by contradiction, together with Liouville’s theorem. Suppose \(P(z)\) does not have a zero. Then
- \(f(z) = 1/P(z)\) is entire. This is obvious because (by assumption) \(P(z)\) has no zeros.
- \(f(z)\) is bounded. This follows because \(1/P(z)\) goes to 0 as \(|z|\) goes to \(\infty\).
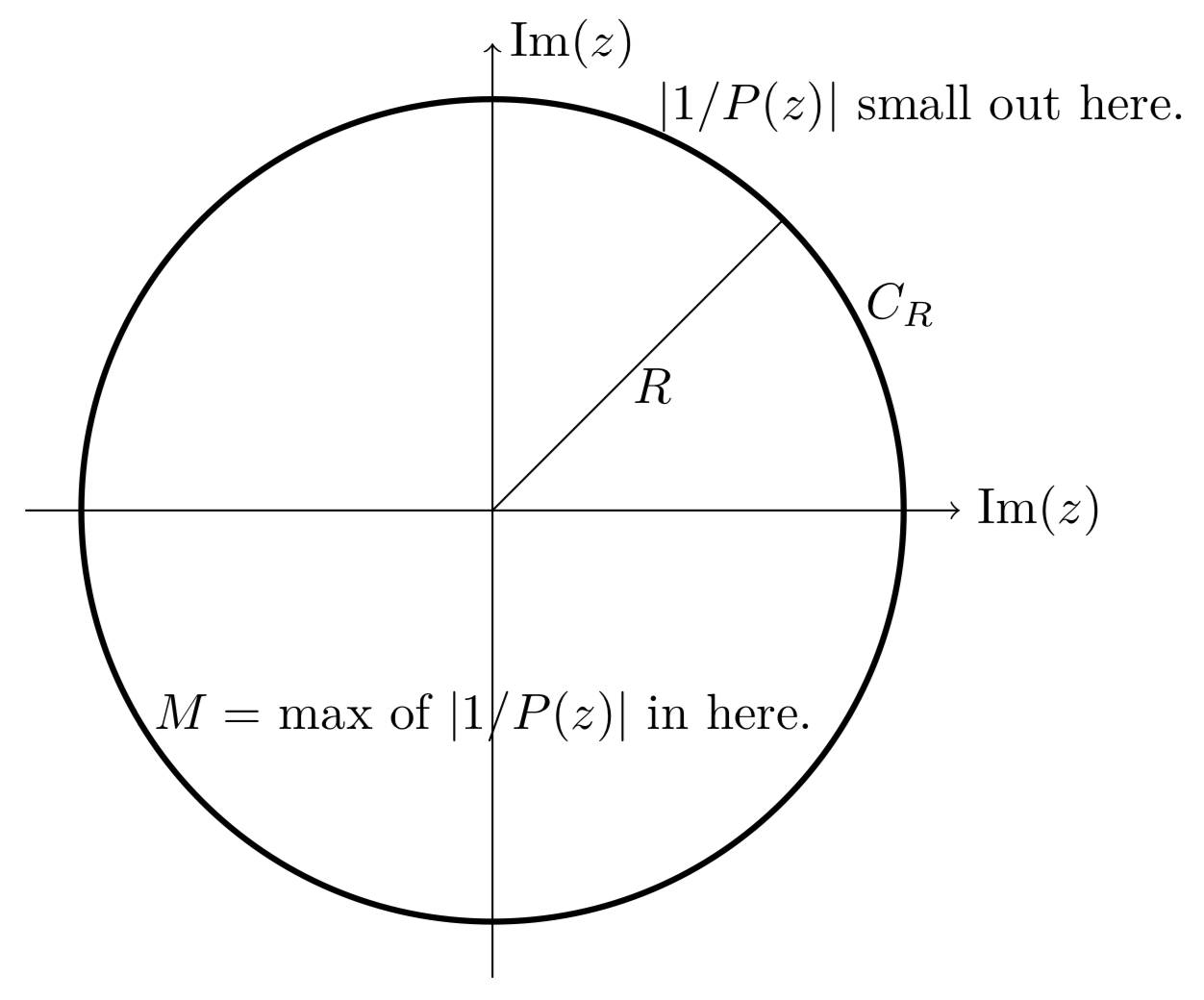
(It is clear that \(|1/P(z)|\) goes to 0 as \(z\) goes to infinity, i.e. \(|1/P(z)|\) is small outside a large circle. So \(|1/P(z)|\) is bounded by \(M\).)
So, by Liouville's theorem \(f(z)\) is constant, and therefore \(P(z)\) must be constant as well. But this is a contradiction, so the hypothesis of “No zeros” must be wrong, i.e. \(P\) must have a zero.
Easy part: \(P\) has exactly \(n\) zeros. Let \(z_0\) be one zero. We can factor \(P(z) = (z - z_0) Q(z)\). \(Q(z)\) has degree \(n - 1\). If \(n -1 > 0\), then we can apply the result to \(Q(z)\). We can continue this process until the degree of \(Q\) is 0.
Maximum modulus principle
Briefly, the maximum modulus principle states that if \(f\) is analytic and not constant in a domain \(A\) then \(|f(z)|\) has no relative maximum in \(A\) and the absolute maximum of \(|f|\) occurs on the boundary of \(A\).
In order to prove the maximum modulus principle we will first prove the mean value property. This will give you a good feel for the maximum modulus principle. It is also important and interesting in its own right.
Suppose \(f(z)\) is analytic on the closed disk of radius \(r\) centered at \(z_0\), i.e. the set \(|z - z_0| \le r\). Then,
\[f(z_0) = \dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta})\ d \theta \nonumber \]
- Proof
-
This is an application of Cauchy’s integral formula on the disk \(D_r = |z - z_0| \le r\).
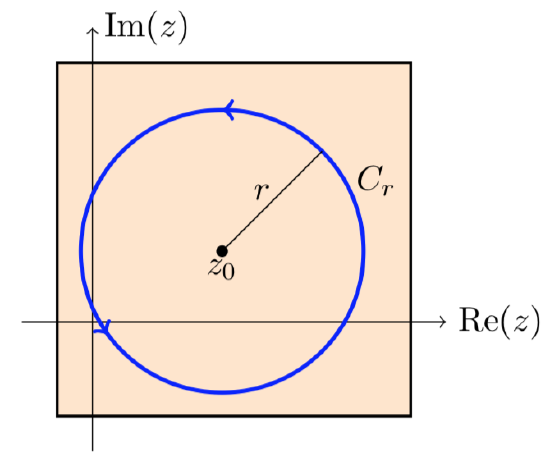
We can parametrize \(C_r\), the boundary of \(D_r\), as
\[\gamma (\theta) = z_0 + re^{i \theta}, \text{ with } 0 \le \theta \le 2\pi, \text{ so } \gamma ' (\theta) = ire^{i \theta}. \nonumber \]
By Cauchy's formula we have
\[f(z_0) = \dfrac{1}{2\pi i} \int_{C_r} \dfrac{f(z)}{z - z_0}\ dz = \dfrac{1}{2\pi i} \int_{0}^{2\pi} \dfrac{f(z_0 + re^{i\theta})}{re^{i \theta}} ire^{i \theta} \ d \theta = \dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta}) \ d\theta \nonumber \]
This proves the property.
In words, the mean value property says \(f(z_0)\) is the arithmetic mean of the values on the circle. Now we can state and prove the maximum modulus principle. We state the assumptions carefully.
When applying this theorem, it is important to verify that the assumptions are satisfied.
Suppose \(f(z)\) is analytic in a connected region \(A\) and \(z_0\) is a point in \(A\).
- If \(|f|\) has a relative maximum at \(z_0\) then \(f(z)\) is constant in a neighborhood of \(z_0\).
- If \(A\) is bounded and connected, and \(f\) is continuous on \(A\) and its boundary, then either \(f\) is constant or the absolute maximum of \(|f|\) occurs only on the boundary of \(A\).
- Proof
-
Part (1): The argument for part (1) is a little fussy. We will use the mean value property and the triangle inequality from Theorem 5.3.2.
Since \(z_0\) is a relative maximum of \(|f|\), for every small enough circle \(C\): \(|z - z_0| = r\) around \(z_0\) we have \(|f(z)| \le |f(z_0)|\) for \(z\) on \(C\). Therefore, by the mean value property and the triangle inequality
\[\begin{array} {rclcc} {|f(z_0)|} & = & {|\dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta}) \ d \theta|} & \ \ \ & {\text{(mean value property)}} \\ {} & \le & {\dfrac{1}{2\pi} \int_{0}^{2\pi} |f(z_0 + re^{i \theta})| \ d \theta} & \ \ \ & {\text{(triangle inequality)}} \\ {} & \le & {\dfrac{1}{2\pi} \int_{0}^{2\pi} |f(z_0)|\ d\theta} & \ \ \ & {(|f(z_0 + re^{i \theta}| \le |f(z_0)|)} \\ {} & = & {|f(z_0)|} & \ \ \ & {} \end{array} \nonumber \]
Since the beginning and end of the above are both \(|f(z_0)|\) all the inequalities in the chain must be equalities.
The first inequality can only be an equality if for all \(\theta\), \(f(z_0 + re^{i\theta})\) lie on the same ray from the origin, i.e. have the same argument or are 0.
The second inequality can only be an equality if all \(|f(z_0 + re^{i \theta})| = |f(z_0)|\). So we have all \(f(z_0 + re^{i \theta})\) have the same magnitude and the same argumeny. This implies they are all the same.
Finally, if \(f(z)\) is constant along the circle and \(f(z_0)\) is the average of \(f(z)\) over the circle then \(f(z) = f(z_0)\)\), i.e. \(f\) is constant on a small disk around \(z_0\).
Part (2): The assumptions that \(A\) is bounded and \(f\) is continuous on \(A\) and its boundary serve to guarantee that \(|f|\) has an absolute maximum (on \(A\) combined with its boundary). Part (1) guarantees that the absolute maximum can not lie in the interior of the region \(A\) unless \(f\) is constant. (This requires a bit more argument. Do you see why?) If the absolute maximum is not in the interior it must be on the boundary.
Find the maximum modulus of \(e^z\) on the unit square with \(0 \le x, y \le 1\).
Solution
\[|e^{x + iy}| = e^x, \nonumber \]
so the maximum is when \(x = 1\), \(0 \le y \le 1\) is arbitrary. This is indeed on the boundary of the unit square
Find the maximum modulus for \(\sin (z)\) on the square \([0, 2\pi] \times [0, 2\pi]\).
Solution
We use the formula
\[\sin (z) = \sin x \cosh y + i \cos x \sinh y. \nonumber \]
So,
\[\begin{array} {rcl} {|\sin (z)|^2} & = & {\sin ^2 x \cosh ^2 y + \cos ^2 x \sinh ^2 y} \\ {} & = & {\sin ^2 x \cosh ^2 y + (1 - \sin ^2 x) \sinh ^2 y} \\ {} & = & {\sin ^2 x + \sinh ^2 y} \end{array} \nonumber \]
We know the maximum over \(x\) of \(\sin ^2 (x)\) is at \(x = \pi /2\) and \(x = 3\pi /2\). The maximum of \(\sinh ^2 y\) is at \(y = 2\pi\). So maximum modulus is
\[\sqrt{1 + \sinh ^2 (2\pi)} = \sqrt{\cosh ^2 (2\pi)} = \cosh (2\pi). \nonumber \]
This occurs at the points
\[z = x + iy = \dfrac{\pi}{2} + 2\pi i, \text{ and } z = \dfrac{3\pi}{2} + 2\pi i. \nonumber \]
Both these points are on the boundary of the region.
Suppose \(f(z)\) is entire. Show that if \(\lim_{z \to \infty} f(z) = 0\) then \(f(z) \equiv 0\).
Solution
This is a standard use of the maximum modulus principle. The strategy is to show that the maximum of \(|f(z)|\) is not on the boundary (of the appropriately chosen region), so \(f(z)\) must be constant.
Fix \(z_0\). For \(R > |z_0|\) let \(M_R\) be the maximum of \(|f(z)|\) on the circle \(|z| = R\). The maximum modulus theorem says that \(|f(z_0)| < M_R\). Since \(f(z)\) goes to 0, as \(R\) goes to infinity, we must have \(M_R\) also goes to 0. This means \(|f(z_0)| = 0\). Since this is true for any \(z_0\), we have \(f(z) \equiv 0\).
Here is an example of why you need \(A\) to be bounded in the maximum modulus theorem. Let \(A\) be the upper half-plane
\[\text{Im} (z) > 0. \nonumber \]
So the boundary of \(A\) is the real axis.
Let \(f(z) = e^{-iz}\). We have
\[|f(x)| = |e^{-ix}| = 1 \nonumber \]
for \(x\) along the real axis. Since \(|f(2i)| = |e^2| > 1\), we see \(|f|\) cannot take its maximum along the boundary of \(A\).
Of course, it can’t take its maximum in the interior of \(A\) either. What happens here is that \(f(z)\) doesn’t have a maximum modulus. Indeed \(|f(z)|\) goes to infinity along the positive imaginary axis.


