17.4: Quantitative Analysis
- Page ID
- 7757
When we are working with a large number of variables that describe aspects of some phenomenon (e.g. items on a test as multiple measures of the underlying trait of "mastery of subject matter"), we often focus our attention on what these multiple measures have "in common". Using information about the co-variation among the multiple measures, we can infer an underlying dimension or factor; once we've done that, we can locate our observations along this dimension. The approach of locating, or scoring, individual cases in terms of their scores on factors of the common variance among multiple indicators is the goal of factor and components analysis (and some other less common scaling techniques).
If we think about our two-mode problem, we could apply this "scaling" logic to either actors or to events. That is, we could "scale" or index the similarity of the actors in terms of their participation in events - but weight the events according to common variance among them. Similarly, we could "scale" the events in terms of the patterns of co-participation of actors - but weight the actors according to their frequency of co-occurrence. Techniques like Tools>MDS and factor or principal components analysis could be used to "scale" either actors or events.
It is also possible to apply these kinds of scaling logics to actor-by-event data. UCINET includes two closely-related factor analytic techniques (Tools>2-Mode Scaling>SVD and Tools>2-Mode Scaling Factor Analysis) that examine the variance in common among both actors and events simultaneously. UCINET also includes Tools>2-Mode Scaling>Correspondence which applies the same logic to binary data. Once the underlying dimensions of the joint variance have been identified, we can then "map" both actors and events into the same "space". This allows us to see which actors are similar in terms of their participation in events (that have been weighted to reflect common patterns), which events are similar in terms of what actors participate in them (weighted to reflect common patterns), and which actors and events are located "close" to one another.
It is sometimes possible to interpret they underlying factors or dimensions to gain insights into why actors and events go together in the ways that they do. More generally, clusters of actors and events that are similarly located may form meaningful "types" or "domains" of social action.
Below, we will very briefly apply these tools to the data on large donors to California initiatives in the 2000-2004 period. Our goal is to illustrate the logic of 2-mode scaling. The discussion here is very short on technical treatments of the (important) differences among the techniques.
Two-Mode SVD Analysis
Singular value decomposition (SVD) is one method of identifying the factors underlying two-mode (valued) data. The method of extracting factors (singular values) differs somewhat from conventional factor and component analysis, so it is a good idea to examine both SVD and 2-mode factoring results.
To illustrate SVD, we have input a matrix of 23 major donors (those who gave a combined total of more than $1,000,000 to five or more campaigns) by 44 California ballot initiatives. Each actor is scored as -1 if they contributed in opposition to the initiative, +1 if they contributed in favor of the initiative, or 0 if they did not contribute. The resulting matrix is valued data that can be examined with SVD and factor analysis; however, the low number of contributors to many initiatives, and the very restricted variance of the scale are not ideal.
Figure 17.6 shows the "singular values" extracted from the rectangular donor-by-initiative matrix using Tools>2-Mode Scaling>SVD.
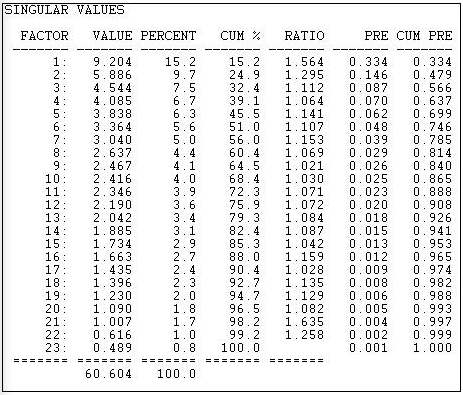
Figure 17.6: Two-mode scaling of California donors and initiatives by Single Value Decomposition: Singular values
The "singular values" are analogous to "eigenvalues" in the more common factor and components scaling techniques. The result here shows that the joint "space" of the variance among donors and initiatives is not well captured by a simple characterization. If we could easily make sense of the patterns with ideas like "left/right" and "financial/moral" as underlying dimensions, there would be only a few singular values that explained substantial portions of the joint variance. This result tells us that the ways that actors and events "go together" is not clean, simple, and easy - in this case.
With this important caveat in mind, we can examine how the events and donors are "scaled" or located on the underlying dimensions. First, the ballot initiatives. Figure 17.7 shows the location, or scale scores of each of the ballot propositions on the first six underlying dimensions of this highly multidimensional space.

Figure 17.7: SVD of California donors and initiatives: Scaling of initiatives
It turns out that the first dimension tends to locate initiatives supporting public expenditure for education and social welfare toward one pole, and initiatives supporting limitation of legislative power toward the other - though interpretations like this are entirely subjective. The second and higher dimensions seem to suggest that initiatives can also be seen as differing from one another in other ways.
At the same time, the results let us locate or scale the donors along the same underlying dimensions. These loadings are shown in Figure 17.8.
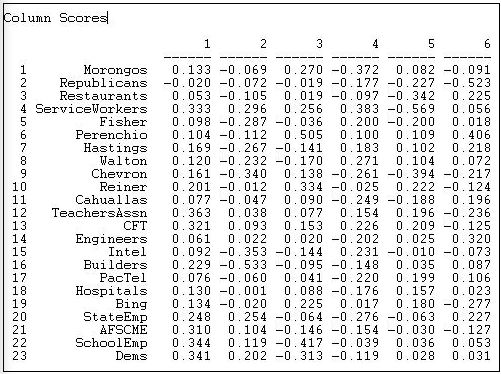
Figure 17.8: SVD of California donors and initiatives: Scaling of donors
Toward the positive end of dimension one (which we earlier interpreted as favoring public expenditure) we find the Democratic party, public employees, and teachers unions; at the opposite pole, we find Republicans and some business and professional groups.
It is often useful to visualize the locations of the actors and events in a scatterplot defined by scale scores on the various dimensions. The map in Figure 17.9 shows the results for the first two dimensions of this space.

Figure 17.9: SVD of California donors and initiatives: Two-dimensional map
We note that the first dimension (left-right in the figure) seems to have its poles "anchored" by differences among the initiatives; the second dimension (top-bottom) seems to be defined more by differences among groups (with the exception of proposition 56). The result does not cleanly and clearly locate particular events and particular actors along strong linear dimensions. It does, however, produce some interesting clusters that show groups of actors along with the issues that are central to their patterns of participation. The Democrats and unions cluster (upper right) along with a number of particular propositions in which they were highly active (e.g. 46, 63). Corporate, building, and venture capitalist cluster (more loosely) in the lower right, along with core issues that formed their primary agenda in the initiative process (e.g. prop 62).
Two-Mode Factor Analysis
Factor analysis provides an alternative method to SVD to accomplish the same goals: identifying underlying dimensions of the joint space of actor-by-event variance, and locating or scaling actors and events in that space. The method used by factor analysis to identify the dimensions differs from SVD. Figure 17.10 shows the eigenvalues (by principle components) calculated by Tools>2-Mode Scaling>Factor Analysis.
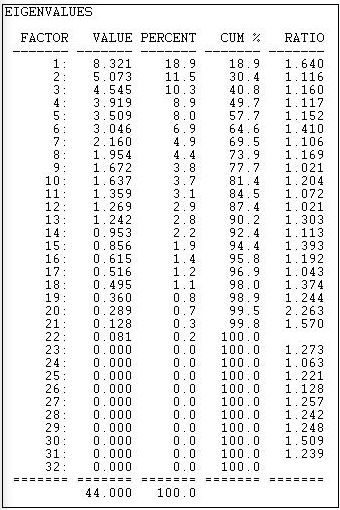
Figure 17.10: Eigenvalues of two-mode factoring of California donors and initiatives
This solution, although different from SVD, also suggests considerable dimensional complexity in the joint variance of actors and events. That is, simple characterizations of the underlying dimensions (e.g. "left/right") do not provide very accurate predictions about the locations of individual actors or events. The factor analysis method does produce somewhat lower complexity than SVD.
With the caveat of pretty poor fit of a low-dimensional solution in mind, let's examine the scaling of actors on the first three factors (Figure 17.11)
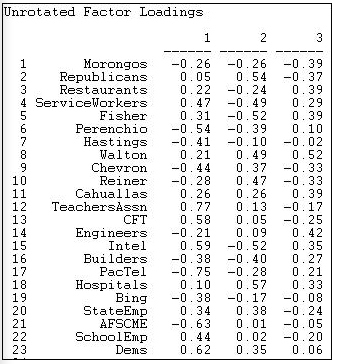
Figure 17.11: Loadings of donors
The first factor, by this method, produces a similar pattern to SVD. At one pole are Democrats and unions, at the other lie many capitalist groups. There are, however, some notable differences (e.g. AFSCME). Figure 17.12 shows the loadings of the events.
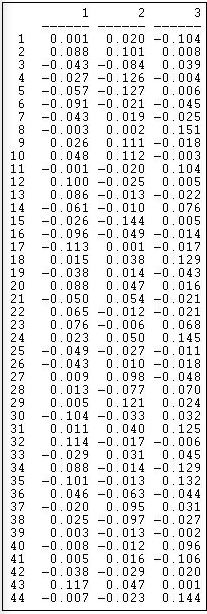
Figure 17.12: Loadings of events
The patterns here also have some similarity to the SVD results, but do differ considerably in the specifics. To visualize the patterns, the loadings of actors and events on the dimensions could be extracted from output data files, and graphed using a scatterplot.
Two-Mode Correspondence Analysis
For binary data, the use of factor analysis and SVD is not recommended. Factoring methods operate on the variance/covariance or correlation matrices among actors and events. When the connections of actors to events is measured at the binary level (which is very often the case in network analysis) correlations may seriously understate covariance and make patterns difficult to discern.
As an alternative for binary actor-by-event scaling, the method of correspondence analysis (Tools>2-Mode Scaling>Correspondence) can be used. Correspondence analysis (rather like Latent Class Analysis) operates on multivariate binary cross-tabulations, and its distributional assumptions are better suited to binary data.
To illustrate the application of correspondence analysis, we've dichotomized the political donor and initiatives data by assigning a value of 1 if an actor gave a donation either in favor or against an initiative, and assigning a zero if they did not participate in the campaign of a particular initiative. If we wanted our analysis to pay attention to partisanship, rather than simple participation, we could have created two datasets - one based on opposition or not, one based on support or not - and done two separate correspondence analyses.
Figure 17.13 shows the location of events (initiatives) along three dimensions of the joint actor-event space identified by the correspondence analysis method.

Figure 17.13: Event coordinates for co-participation of donors in California initiative campaigns
Since these data do not reflect partisanship, only participation, we would not expect the findings to parallel those discussed in the sections above. And, they don't. We do see, however, that this method also can be used to locate the initiatives along multiple underlying dimensions that capture variance in both actors and events. Figure 17.14 shows the scaling of the actors.
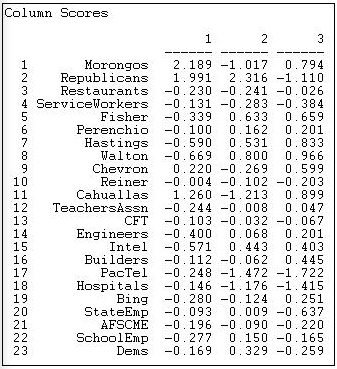
Figure 17.14: Actor coordinates for co-participation of donors in California initiative campaigns
The first dimension here does have some similarity to the Democrat/union versus capitalist poles. Here, however, this difference means that the two groupings tend to participate in different groups of initiatives, rather than confronting one another in the same campaigns.
Visualization is often the best approach to finding meaningful patterns (in the absence of a strong theory). Figure 17.15 shows the plot of the actors and events in the first two dimensions of the joint correspondence analysis space.

Figure 17.15: Correspondence analysis two-dimensional map
The lower right quadrant here contains a meaningful cluster of actors and events, and illustrates how the results of correspondence analysis can be interpreted. In the lower right we have some propositions regarding Indian casino gambling (68 and 70) and two propositions regarding ecological/conservation issues (40 and 50). Two of the major Native American Nations (the Cahualla and Morongo bands of Mission Indians) are mapped together. The result is showing that there is a cluster of issues that "co-occur" with a cluster of donors - actors defining events, and events defining actors.


