8.6: Group-External and Group-Internal Ties
- Page ID
- 7698
Actors may be embedded in macro-structures, as well as in dyads, triads, and neighborhoods. Some macro-structures are social agents (like voluntary and formal organizations); some macro-structures are categorical units (like gender and ethnic groups). To understand the "texture" of the "social fabric" we might want to index the extent to which these macro-structures "cluster" the interaction patterns of individuals who fall within them.
Krackhardt and Stern (1988) developed a very simple and useful measure of the group embedding based on comparing the numbers of ties within groups and between groups. The E-I (external-internal) index takes the number of ties of group members to outsides, subtracts the number of ties to other group members, and divides by the total number of ties. The resulting index ranges from -1 (all ties are internal to the group) to +1 (all ties are external to the group). Since this measure is concerned with any connection between members, the directions of ties are ignored (i.e. either an out-tie or an in-tie constitutes a tie between two actors).
The E-I index can be applied at three levels: the entire population, each group, and each individual. That is, the network as a whole (all the groups) can be characterized in terms of the bounded-ness and closure of its sub-populations. We can also examine variation across the groups in their degree of closure; and, each individual can be seen as more or less embedded in their group.
Here's a sample of the dialog with Network>Cohesion>E-I Index in which we examine the Knoke information network that has been partitioned according to the attribute of organizational type (group 1 = governmental generalists, group 2 = non-governmental generalists, group 3 = welfare specialists).
Figure 8.10: Dialog of Network>Cohesion>E-I Index
The range of possible values of the E-I index is restricted by the number of groups, relative group sizes, and total number of ties in a graph. Often this range restriction is quite severe, so it is important to re-scale the coefficient to range between the maximum possible degree of "external-ness" (+1) and the maximum possible degree of "internal-ness" (-1). As Blau and others have noted, the relative sizes of sub-populations have dramatic consequences for the degree of internal and external contacts, even when individuals may choose contacts at random.
To assess whether a given E-I index value is significantly different than what would be expected by random mixing (i.e. no preference for within or without group ties by group members), a permutation test is performed by Network>Cohesion>E-I Index. A large number of trials are run in which the block of groups is maintained, and the overall density of ties is maintained, but the actual ties are randomly distributed. From a large number of trials (the default is 5000), a sampling distribution of the numbers of internal and external ties - under the assumption that ties are randomly distributed - can be calculated. This sampling distribution can then be used to assess the frequency with which the observed result would occur by sampling from a population in which ties are randomly distributed.
Let's look first at the results for the graph as a whole, in Figure 8.11.
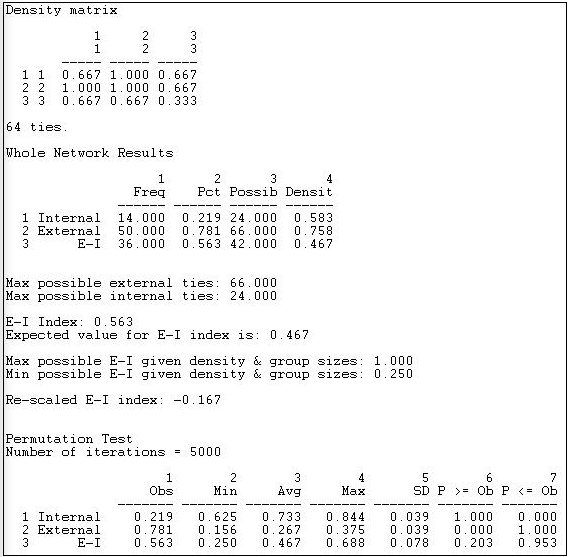
Figure 8.11: E-I index output for the Knoke information network - whole network
The observed block densities are presented first. Since any tie (in or out) is regarded as a tie, the densities in this example are quite high. The densities off the main diagonal (out-group ties) appear to be slightly more prevalent than the densities on the main diagonal (in-group ties).
Next, we see the numbers of internal ties (14, or \(22\%\)) and external ties (50, or \(78\%\)) that yield a raw (not re-scaled) E-I index of +0.563. That is, a preponderance of external over internal ties for the graph as a whole. Also shown are the maximum possible numbers of internal and external ties given the group sizes and density. Note that, due to these constraints, the result of a preponderance of external ties is not unexpected - under a random distribution, the E-I index would be expected to have a value of +0.467, which is not very much different from the observed value.
We see that, given the group sizes and density of the graph, the maximum possible value of the index (+1.0) and its minimum value (+0.25) are both positive. If we re-scale the observed value of the E-I index (+0.563) to fall into this range, we obtain a re-scaled index value of -0.167. This suggests that, given the demographic constraints and overall density, there is a very modest tendency toward group closure.
The last portion of the results gives the values of the permutation-based sampling distribution. Most important here is the standard deviation of the sampling distribution of the index, or its standard error (0.078). This suggests that the value of the raw index is expected to vary by this much from trial to trial (on average) just by chance. Given this result, we can compare the observed value in our sample (+0.563) to the expected value (+0.467) relative to the standard error. The observed difference of about 0.10 could occur fairly frequently just by sampling variability (p = 0.203). Most analysts would not reject the null hypothesis that the deviation from randomness was not "significant". That is, we cannot be confident that the observed mild bias toward group closure is not random variation.
The E-I index can also be calculated for each group and for each individual. These index numbers describe the tendencies toward group closure of each of the groups, and the propensity of each individual to have ties within their group. Figure 8.12 displays the results.
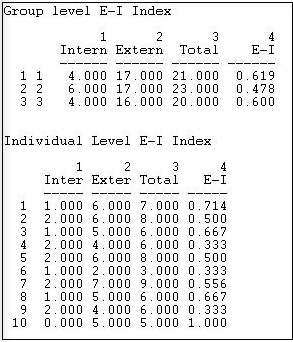
Figure 8.12: E-I index output for the Knoke information network - groups and individuals
The first panel of Figure 8.12 shows the raw counts of ties within and without each of the three types of organizations, and the E-I index for each group. Governmental generalists (group 2) appear to be somewhat more likely to have out-group ties than either of the other sub-populations. The relatively small difference, though, should be treated with considerable caution given the sampling variability (we cannot directly apply the standard error estimate for the whole graph to the results for sub-populations or individuals, but they are suggestive). We should also note that the E-I results for groups and individuals are in "raw" form, and not "re-scaled".
There is considerable variability across individuals in their propensity to in-group ties, as can be seen in the last panel of the results. Several actors (4, 6, 9) tend toward closure - having a preponderance of ties within their own group; a couple others (10, 1) tend toward a preponderance of ties outside their groups.


