11.1: Definition of Cellular Automata
- Page ID
- 7829
“Automaton” (plural: “automata”) is a technical term used in computer science and mathematics for a theoretical machine that changes its internal state based on inputs and its previous state. The state set is usually defined as finite and discrete, which often causes nonlinearity in the system’s dynamics.
Cellular automata (CA) [18] are a set of such automata arranged along a regular spatial grid, whose states are simultaneously updated by a uniformly applied state-transition function that refers to the states of their neighbors. Such simultaneous updating is also called synchronous updating (which could be loosened to be asynchronous; to be discussed later). The original idea of CA was invented in the 1940s and 1950s by John von Neumann and his collaborator Stanisław Ulam. They invented this modeling framework, which was among the very first to model complex systems, in order to describe self-reproductive and evolvable behavior of living systems [11].
Because CA are very powerful in describing highly nonlinear spatio-temporal dynamics in a simple, concise manner, they have been extensively utilized for modeling various phenomena, such as molecular dynamics, hydrodynamics, physical properties of materials, reaction-diffusion chemical processes, growth and morphogenesis of a living organism, ecological interaction and evolution of populations, propagation of traffic jams, social and economical dynamics, and so forth. They have also been utilized for computational applications such as image processing, random number generation, and cryptography.
There are some technical definitions and terminologies you need to know to discuss CA models, so here comes a barrage of definitions.
Mathematically speaking, CA are defined as a spatially distributed dynamical system where both time and space are discrete. A CA model consists of identical automata (cells or sites) uniformly arranged on lattice points in a D-dimensional discrete space (usually \(D = 1, 2,\) or \(3)\). Each automaton is a dynamical variable, and its temporal change is given by
\[s_{t+1}(x)=F(s_{t}(x+x_{0}), s_{t}(x+x_{1}), ..., s_{t}(x+x_{n-1})), \label{(11.1)} \]
where \(s_{t}(x)\) is the state of an automaton located at \(x\) at time \(t\), \(F\) is the state-transition function, and \(N = {x_0,x_1,...,x_{n−1}}\) is the neighborhood. The idea that the same statetransition function and the same neighborhood apply uniformly to all spatial locations is the most characteristic assumption of CA. When von Neumann and Ulam developed this modeling framework, researchers generally didn’t have explicit empirical data about how things were connected in real-world complex systems. Therefore, it was a reasonable first step to assume spatial regularity and homogeneity (which will be extended later in network models).
\(s_t\) is a function that maps spatial locations to states, which is called a configuration of the CA at time \(t\). A configuration intuitively means the spatial pattern that the CA display at that time. These definitions are illustrated in Fig. 11.1.1.
Neighborhood \(N\) is usually set up so that it is centered around the focal cell being updated \((x_0 = 0)\) and spatially localized \((|x_i −x_0| ≤ r\) for \(i = 1,2,...,n−1)\), where r is called a radius of \(N\). In other words, a cell’s next state is determined locally according to its own current state and its local neighbors’ current states. A specific arrangement of states within the neighborhood is called a situation here. Figure 11.1.2 shows typical examples of neighborhoods often used for two-dimensional CA. In CA with von Neumann neighborhoods (Fig. 11.1.2, left), each cell changes its state according to the states of its upper, lower, right, and left neighbor cells as well as itself. With Moore neighborhoods (Fig. 11.1.2, right), four diagonal cells are added to the neighborhood.
The state-transition function is applied uniformly and simultaneously to all cells in the space. The function can be described in the form of a look-up table (as shown in Fig. 11.1.1), some mathematical formula, or a more high-level algorithmic language.
If a state-transition function always gives an identical state to all the situations that are identical to each other when rotated, then the CA model has rotational symmetry. Such symmetry is often employed in CA with an aim to model physical phenomena. Rotational symmetry is called strong if all the states of the CA are orientation-free and if the rotation of a situation doesn’t involve any rotation of the states themselves (Fig. 11.1.3, left). Otherwise, it is called weak (Fig. 11.1.3, right). In CA with weak rotational symmetry, some states are oriented, and the rotation of a situation requires rotational adjustments of those states as well. Von Neumann’s original CA model adopted weak rotational symmetry.
If a state-transition function depends only on the sum of the states of cells within the neighborhood, the CA is called totalistic. By definition, such state-transition functions are rotationally symmetric. The totalistic assumption makes the design of CA models much simpler, yet they can still produce a wide variety of complex dynamics [34].
The states of CA are usually categorized as either quiescent or non-quiescent. A cell in a quiescent state remains in the same state if all of its neighbors are also in the same quiescent state. Many CA models have at least one such quiescent state, often represented by either “0” or “ ” (blank). This state symbolizes a “vacuum” in the CA universe. Non-quiescent states are also called active states, because they can change dynamically and interact with nearby states. Such active states usually play a primary role in producing complex behaviors within CA.
Because CA models have a spatial extension as well as a temporal extension, you need to specify spatial boundary conditions in addition to initial conditions in order to study their behaviors. There are several commonly adopted boundary conditions:
This assumes that the space is infinite and completely filled with the quiescent state
This assumes that the space is “wrapped around” each spatial axis, i.e., the cells at one edge of a finite space are connected to the cells at the opposite edge. Examples include a ring for 1-D CA and a torus for 2-D CA
This assumes that cells at the edge of a finite space don’t have neighbors beyond the boundaries. This necessarily results in fewer numbers of neighbors, and therefore, the state-transition function must be designed so that it can handle such cases.
This assumes that cells at the edge of a finite space have fixed states that will never change. This is often the easiest choice when you implement a simulation code of a CA model
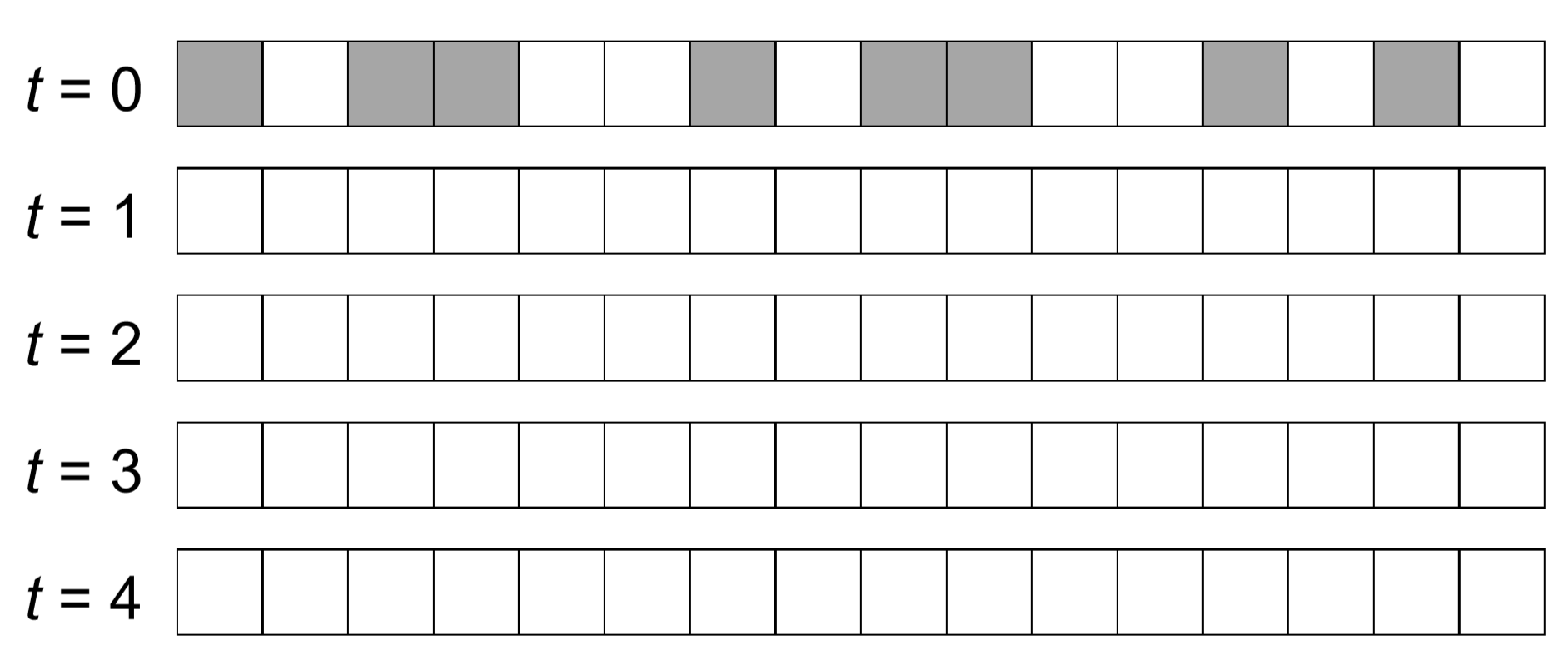
Shown below is an example of a one-dimensional totalistic CA model with radius 1 and a periodic boundary condition. White means 0, while gray means 1. Each cell switches to round(S/3) in every time step, where S is the local sum of states within its neighborhood. Complete the time evolution of this CA.
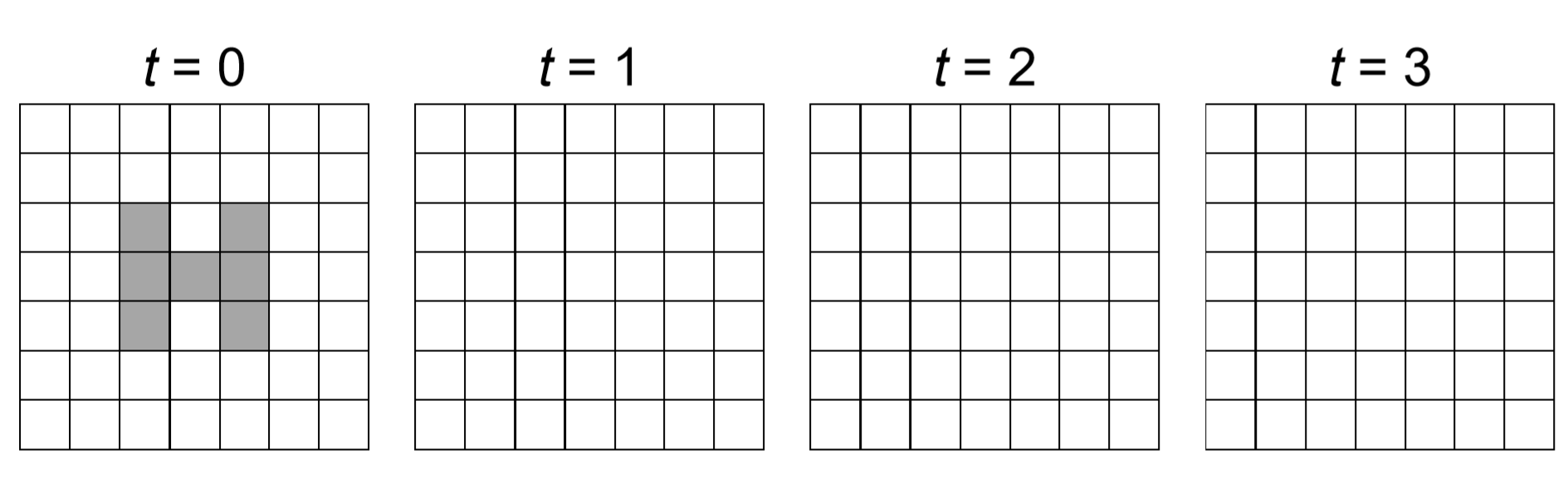
Shown below is an example of a two-dimensional totalistic CA model with von Neumann neighborhoods and with no boundary (infinite space) conditions. White means 0 (= quiescent state), while gray means 1. Each cell switches to round(S/5) in every time step, where S is the local sum of the states within its neighborhood. Complete the time evolution of this CA.