15.4: Visualizing Networks with NetworkX
- Page ID
- 7860
NetworkX also provides functions for visualizing networks. They are not as powerful as other more specialized software1, but still quite handy and useful, especially for small- to mid-sized network visualization. Those visualization functions depend on the functions defined in matplotlib (pylab), so we need to import it before visualizing networks.
The simplest way is to use NetworkX’s draw function:

The result is shown in Fig. 15.4.1. Red circles represent the nodes, and the black lines connecting them represent the edges. By default, the layout of the nodes and edges is automatically determined by the Fruchterman-Reingold force-directed algorithm [62] (called “spring layout” in NetworkX), which conducts a pseudo-physics simulation of the movements of the nodes, assuming that each edge is a spring with a fixed equilibrium distance. This heuristic algorithm tends to bring groups of well-connected nodes closer to each other, making the result of visualization more meaningful and aesthetically more pleasing.
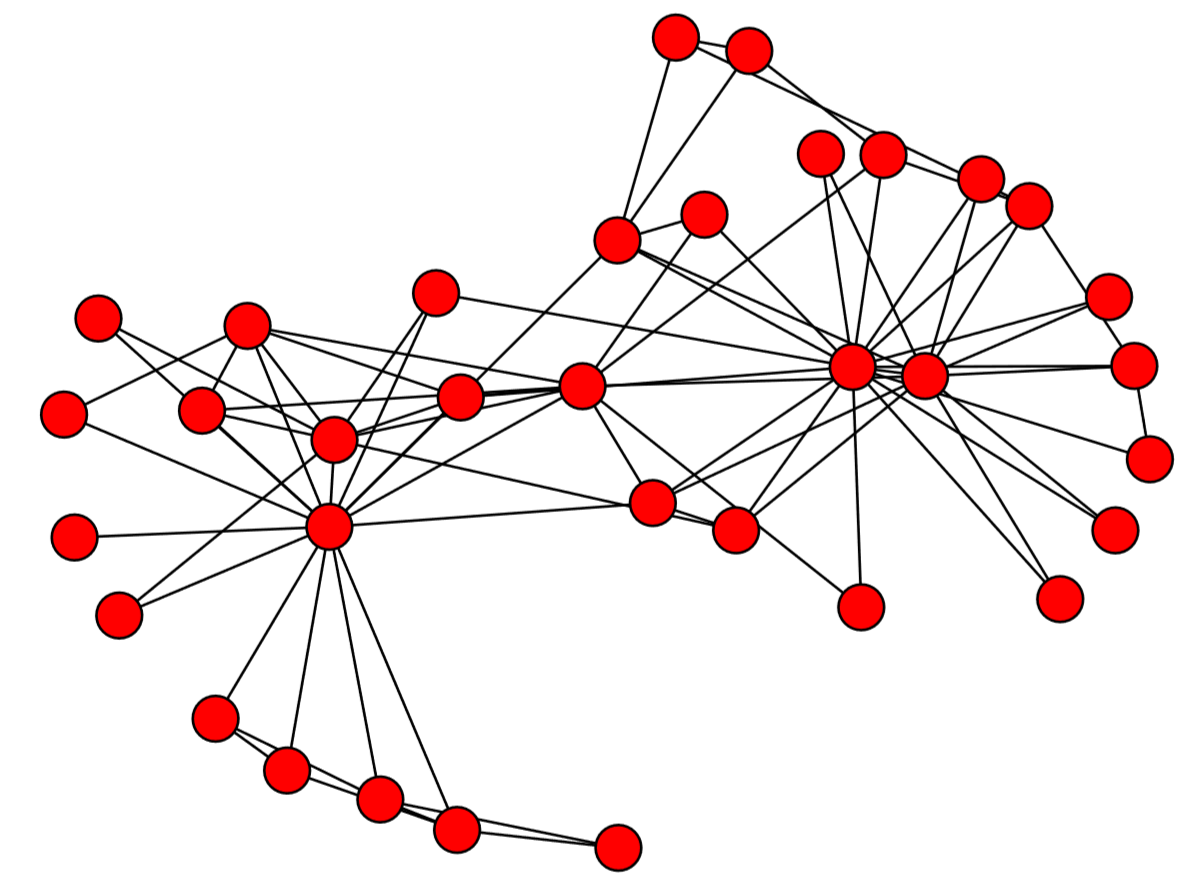
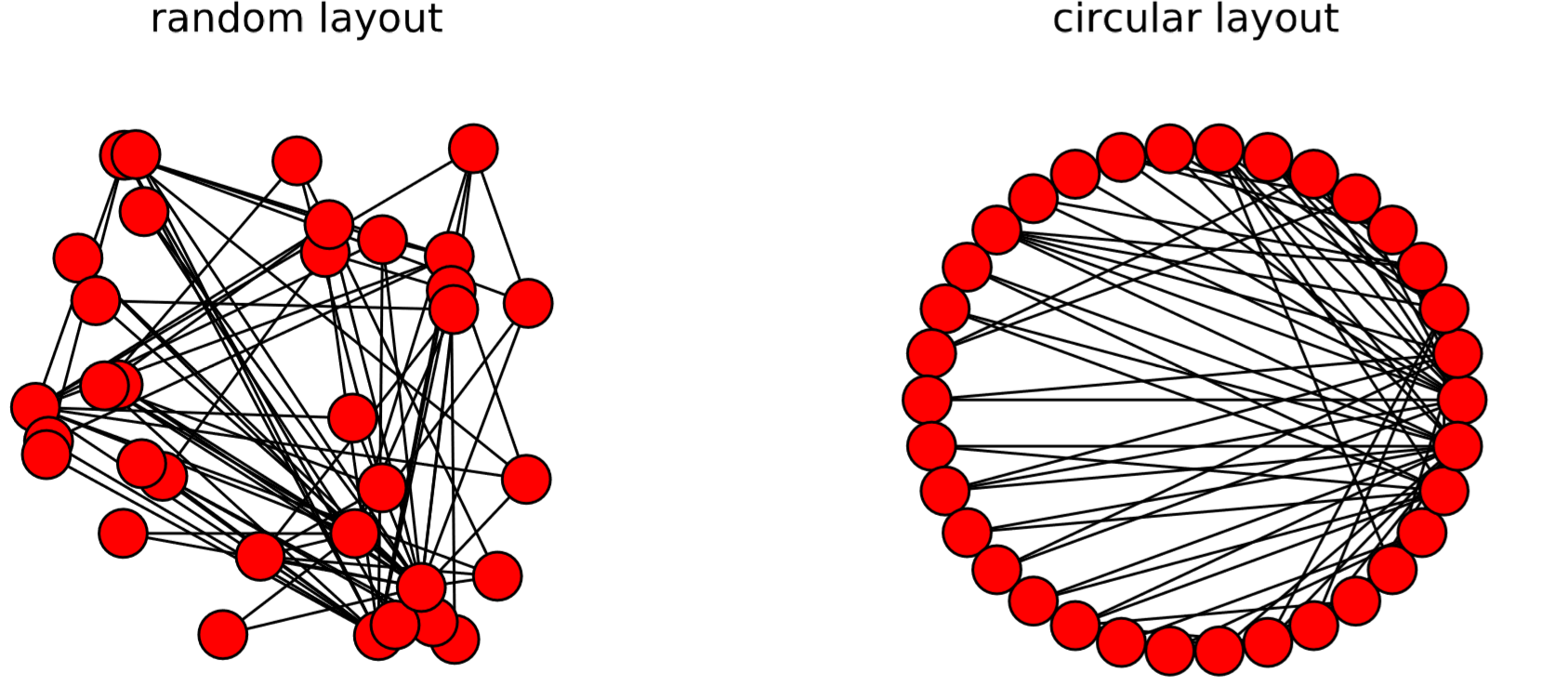
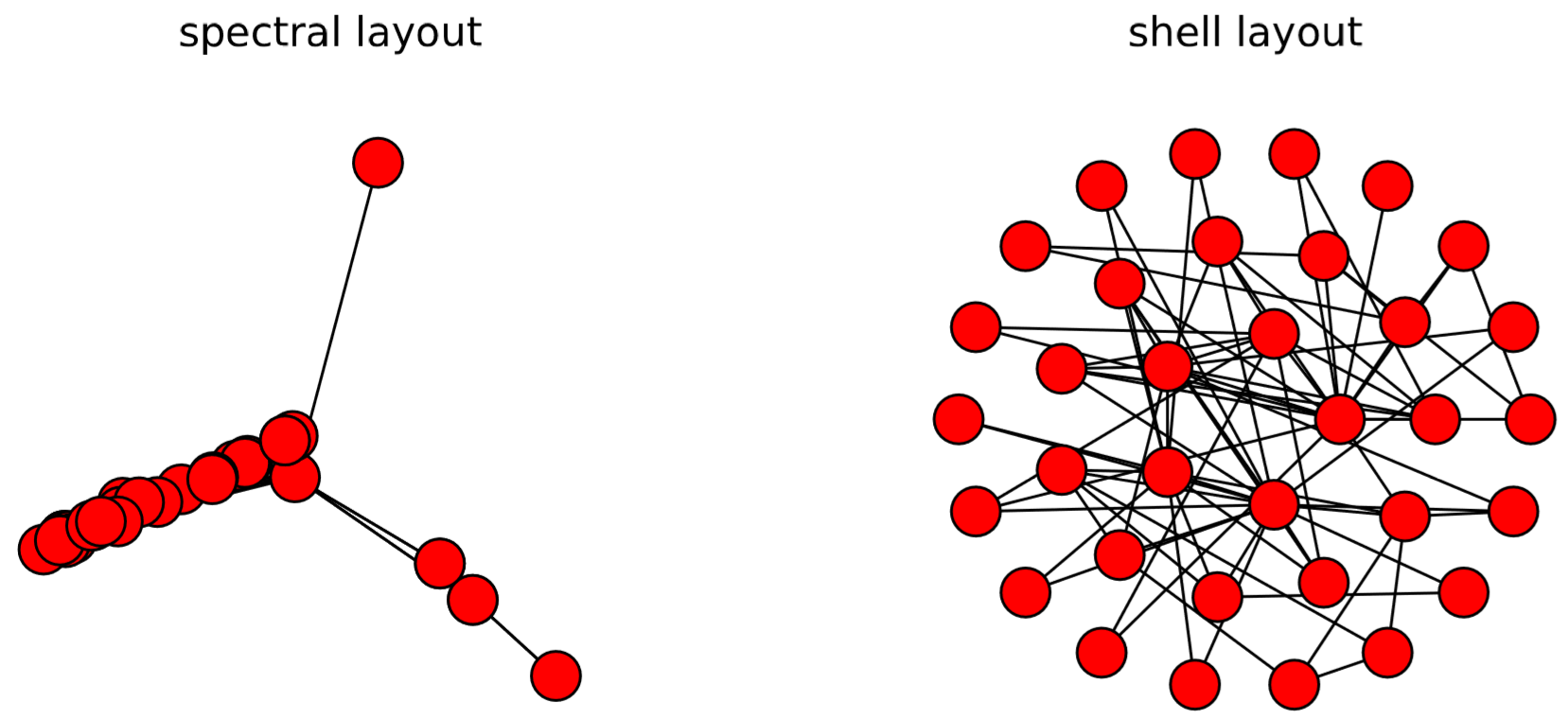
There are several other layout algorithms, as shown in Code 15.12 and Fig.15.5.1. Also, there are many options you can use to customize visualization results (see Code 15.13 and Fig. 15.4.3). Check out NetworkX’s online documentation to learn more about what you can do.





Visualize the following graphs. Look them up in NetworkX’s online documentation to learn how to generate them.
• A “hypercube graph” of four dimensions.
• A “ladder graph” of length 5.
• A “barbell graph” made of two 20-node complete graphs that are connected by a single edge.
• A “wheel graph” made of 100 nodes.
Visualize the social network you created in Exercise 15.3.2. Try several options to customize the result to your preference.
1For example, Gephi (http://gephi.github.io/) can handle much larger networks, and it has many more node-embedding algorithms than NetworkX.


