3.10: Division Explorations
- Page ID
- 10384
Anu refuses to tell anyone if she is working in a 1←10 system, or a 1←5 system, or any other system. She makes everyone call it a 1 ← x system but won’t tell anyone what x stands for.
We know that boxes in a 1←10 have values that are powers of ten: 1, 10, 100, 1000, 10000…
And boxes in a 1←5 system are powers of five: 1, 5, 25, 125, 625…
So Anu’s system, whatever it is, must be powers of x: \(1, x, x^{2}, x^{3}, x^{4} \ldots\)
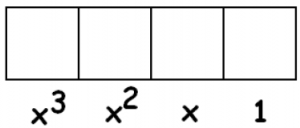
\[2x^{3} + 5x^{2} + 5x + 6 \ldotp \nonumber \]
And when she writes \(12_{x}\) she means:
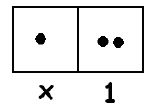
\[x + 2 \ldotp \nonumber \]
Anu decides to compute \(2556_{x} \div 12_{x}\).
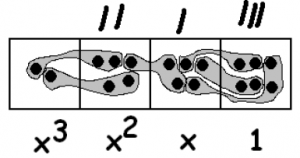
She obtains:
\[(2x^{3} + 5x^{2} + 5x + 6) \div (x + 2) = 2x^{2} + x + 3 \ldotp \nonumber \]
- Check Anu’s division by computing the product $$(x + 2)(2x^{2} + x + 3) \ldotp$$Did it work?
- Use Anu’s method to find $$(3x^{2} + 7x + 2) \div (x + 2) \ldotp$$
- Use Anu’s method to find $$(2x^{4} + 3x^{3} + 5x^{2} + 4x + 1) \div (2x + 1) \ldotp$$
- Use Anu’s method to find $$(x^{4} + 3x^{3} + 6x^{2} + 5x + 3) \div (x^{2} + x + 1) \ldotp$$
Anu later tells use that she really was thinking of a 1←10 system so that xdoes equal ten. Then her number 2556 really was two thousand, five hundred and fifty six and 12 really was twelve. Her statement:
\[(2x^{3} + 5x^{2} + 5x + 6) \div (x + 2) = 2x^{2} + x + 3 \ldotp \nonumber \]
is actually 2556 : 12 = 213.
- Check that 2556 : 12 = 213 is correct in base 10.
- Keeping with the 1←10 system, what division problems did you actually solve in parts (b), (c), and (d) of Problem 28? Check that your answers are correct.
Uh Oh! Anu has changed her mind. She now says she was thinking of a 1←11 system.
Now \(2556_{x}\) means \(2 \cdot 11^{3} + 5 \cdot 11^{2} + 5 \cdot 11 + 6 = 3328_{ten}\).
Similarly, \(12_{x}\) means \(1 \cdot 11 + 2 = 13_{ten}\), and \(213_{x}\) means \(2 \cdot 11^{2} + 1 \cdot 11 + 3 = 256_{ten}\).
So Anu’s computation \(2556_{x} \div 12_{x}\ = 213_{x}\) is actually the (base 10) statement: \[3328 : 13 = 256 \ldotp \nonumber \]
- Check that 3328 : 13 = 256 is also correct in base ten.
- Keeping with the 1←11 system, what division problems did you actually solve in parts (b), (c), and (d) of Problem 28? Check that they are correct.
- Use Anu’s method to show that $$(x^{4} + 4x^{3} + 6x^{2} + 4x + 1) \div (x + 1) = (x^{3} + 3x^{2} + 3x + 1) \ldotp$$
- What is this saying for x = 10? Check that the division is correct.
- What is this saying for x = 2? Check that the division is correct.
- What is this saying for x equal to each of 3, 4, 5, 6, 7, 8, 9, and 11? Check that each division is correct.
- What is this saying for x = 0?


