5.3: Careful Use of Language in Mathematics- =
- Page ID
- 9851
The notion of equality is fundamental in mathematics, and especially in algebra and algebraic thinking. The symbol “=”’ expresses a relationship. It is not an operation in the way that + and are × operations. It should not be read left-to-right, and it definitely does not mean “… and the answer is …”.
For your work to be clear and easily understood by others, it is essential that you use the symbol = appropriately. And for your future students to understand the meaning of the = symbol and use it correctly, it is essential that you are clear and precise in your use of it.
Let’s start by working on some problems.
Akira went to visit his grandmother, and she gave him $1.50 to buy a treat.
He went to the store and bought a book for $3.20. After that, he had $2.30 left.
How much money did Akira have before he visited his grandmother?
Examine the following equations. Decide: Is the statement always true, sometimes true, or never true? Justify your answers.
- $$5+3=8 \ldotp$$
- $$\frac{2}{3} + \frac{1}{2} = \frac{3}{5} \ldotp$$
- $$5 + 3 = y \ldotp$$
- $$\frac{a}{5} = \frac{5}{a} \ldotp$$
- $$n + 3 = m \ldotp$$
- $$3x = 2x + x \ldotp$$
- $$5k = 5k + 1 \ldotp$$
Consider the equation
\[18 - 7 = \_\_\_ \ldotp \nonumber \]
- Fill in the blank with something that makes the equation always true.
- Fill in the blank with something that makes the equation always false.
- Fill in the blank with something that makes the equation sometimes true and sometimes false.
If someone asked you to solve the equations in Problem 8, what would you do in each case and why?
Kim solved Problem 7 this way this way:
Let’s see:
\[2.30 + 3.20 = 5.50 - 1.50 = 4, \nonumber \]
so the answer is 4.
What do you think about Kim’s solution? Did she get the correct answer? Is her solution clear? How could it be better?
Although Kim found the correct numerical answer, her calculation really doesn’t make any sense. It is true that
\[2.30 + 3.20 = 5.50 \ldotp \nonumber \]
But it is definitely not true that
\[2.30 + 3.20 = 5.50 - 1.40 \ldotp \nonumber \]
She is incorrectly using the symbol “=”, and that makes her calculation hard to understand.
- Can you write a good definition of the symbol “=”? What does it mean and what does it represent?
- Give some examples: When should the symbol “=”’ be used, and when should it not be used?
- Do these two equations express the same relationships or different relationships? Explain your answer. $$x^{2} - 1 = (x + 1)(x - 1) \ldotp$$$$(x+1)(x-1) = x^{2} -1 \ldotp$$
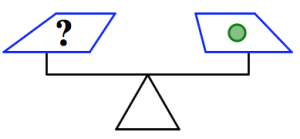
This picture shows a (very simplistic) two-pan balance scale. Such a scale allows you to compare the weight of two objects. Place one object in each pan. If one side is lower than the other, then that side holds heavier objects. If the two sides are balanced, then the objects on each side weigh the same.
In the pictures below:
- The orange triangles all weigh the same.
- The green circles all weigh the same.
- The purple squares all weigh the same.
- The silver stars all weigh the same.
- The scale is balanced.
1. In the picture below, what do you know about the weights of the triangles and the circles? How do you know it?
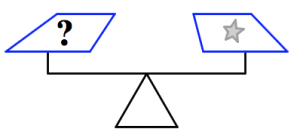
2. In the picture below, what do you know about the weights of the circles and the stars? How do you know it?
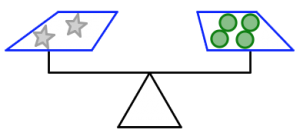
3. In the picture below, what do you know about the weights of the stars and the squares? How do you know it?
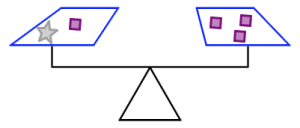
In the pictures below:
- The orange triangles all weigh the same.
- The green circles all weigh the same.
- The purple squares all weigh the same.
- The scale is balanced.
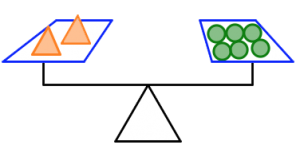
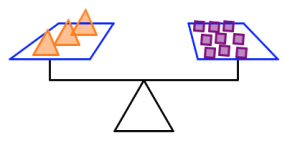

How many purple squares will balance with one circle? Justify your answer.
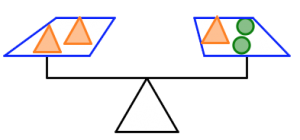
In the pictures below:
- The orange triangles all weigh the same.
- The green circles all weigh the same.
- The purple squares all weigh the same.
- The silver stars all weigh the same.
- The scale is balanced.
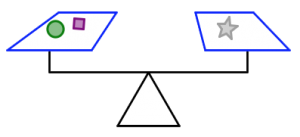
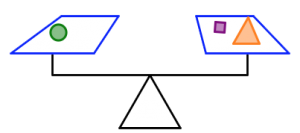
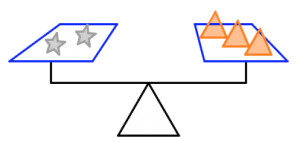
How many purple squares will balance the scale in each case? Justify your answers.
In the pictures below:
- The orange triangles all weigh the same.
- The green circles all weigh the same.
- The purple squares all weigh the same.
- The scale is balanced.
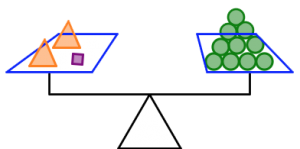
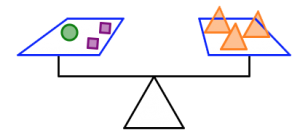
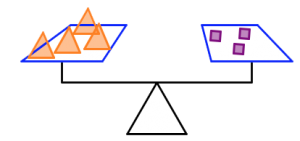
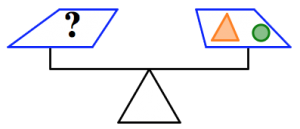
What will balance the last scale? Can you find more than one answer?
In the pictures below:
- The orange triangles all weigh the same.
- The green circles all weigh the same.
- The purple squares all weigh the same.
- The scale is balanced.
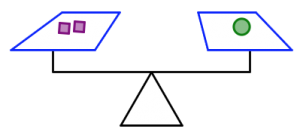
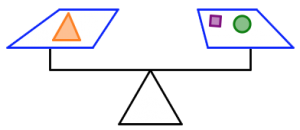
- Which shape weighs the most: the square, the triangle, or the circle? Which shape weighs the least? Justify your answers.
- Which of the two scales is holding the most total weight? How do you know you’re right?
What do Problems 11–14 above have to do with the “=” symbol?