8.4: Navigation
- Page ID
- 9873
The following is from pvs.kcc.hawaii.edu/ike/hookele/modern_wayfinding.html.
A voyage undertaken using modern wayfinding has three components:
Design a course strategy, which includes a reference course for reaching the vicinity of one’s destination, hopefully upwind, so that the canoe can sail downwind to the destination rather than having to tack into the wind to get there. (Tacking involves sailing back and forth as closely as possible into the wind to make progress against the wind; its very arduous and time-consuming, something to be avoided if at all possible, particularly at the end of a long, difficult voyage.)
During the voyage, holding as closely as possible to the reference course while keeping track of (1) distance and direction traveled; (2) one’s position north and south and east and west of the reference course and (3) the distance and direction to the destination.
Finding land after entering the vicinity of the destination, called a target screen or ‘the box’.
So how is the navigation done — especially component (2) — through thousands of miles of open ocean? You can’t see land. How can you hold closely to the reference course? How can you keep track of distance and direction traveled? How can you even know if you’re going in the right direction if all you can see is blue ocean and blue sky?
By day, the navigators use their deep knowledge of the oceans. Which way do the winds blow? Which way do the prevailing currents move? Clouds in the sky, flotsam in the water, and animal behaviors give them great insight into where land might be, and where they are in relation to it.
By night, they use the stars. In this section, you’ll learn just a tiny fraction of what these master navigators know about the stars.
Here is a time-lapse picture[1] of the stars in the night sky:

- Describe what you see happening in this picture.
- What can you conclude about how the stars move through the night sky?
- How might that help a navigator find his way?
Star Compass
A fundamental tool for navigators on Hōkūle`a and other voyaging canoes is a star compass. Here’s a picture of Mau Piailug[2] and a star compass[3] he used in his teaching.


The object in the center of the circle represents the canoe. The shells along the outside represent directional points. The idea is to imagine the stars rising up from the horizon in the east, traveling through the night sky, and setting past the horizon in the west. They move like they’re on a sphere surrounding the Earth (it’s called the celestial sphere).
Nainoa Thompson developed a star compass with 32 equidistant points around a circle. (Note this is different than the points in Mau’s star compass pictured above.) You will first try to make a rough sketch of Nainoa’s star compass based on this information.
- Place 32 points around the circle so they are equally spaced.
- The arcs between these equidistant points are called “houses.” You will label each house with its Hawaiian name. Start with the four cardinal directions:
`Ākau: North.
Hema: South.
Hikina: East.
Komohana: West.
- The four quadrants also get names. (These cover all of the houses in the quadrant, so label them in the appropriate place inside the compass.)
Ko`olau: northeast.
Malani: southeast.
Kona: southwest.
Ho`olua: northwest.
- Moving from `Ākau to Hikina (clockwise), there are seven houses. They are labeled in order as you move away from `Ākau:
Haka: “empty,” describing the skies in this house.
Nā Leo: “the voices” of the stars speaking to the navigator.
Nālani: “the heavens.”
Manu: “bird,” the Polynesian metaphor for a canoe.
Noio: the Hawaiian tern (a bird).
`Āina: “land.”
Lā: “sun,” which stays in this house most of the year.
- The compass has a vertical line of symmetry, so there are the same seven houses in the same order as you move from `Ākau to Komohana (counterclockwise).
- The compass also has a horizontal line of symmetry. Use that fact to label the houses from Hema to Hikina (counterclockwise) and from Hema to Komohana (clockwise).
How is the star compass used in navigation? There are lots of ways. Here’s a (very!) quick overview:
- The canoe is pictured in the middle of the star compass, with all of the houses around.
- Winds and ocean swells move directly across the star compass from north to south or vice versa.
- If the swells are coming from `Āina Ko`olau, they will be heading in the direction `Āina Kona. (Look at your star compass and trace out this path.)
- If the wind is coming from Nālani Malani, it will be heading towards Nālani Ho`olua. (Look at your star compass and trace out this path.)
- Stars stay in their houses, but also in their hemisphere. They do not move across the center of the circle.
- Just like the sun, they rise in the east and set in the west.
- `A`ā (Sirius) rises in Lā Malanai and sets in Lā Kona. (Look at your star compass and trace out this path.)
- Hōkūle`a rises in `Āina Ko`olau and sets in `Āina Ho`olua. (Look at your star compass and trace out this path.)
A navigator memorizes the houses of over 200 stars. At sunrise and sunset (when the sun or the stars are rising), the navigator can use the star compass to memorize which way the wind is moving and which way the currents are moving. The navigator can then use that information throughout the day or night to ensure the canoe stays on course.
Look again at the time-lapse picture of the stars:

- Describe how this shows that stars “stay in their houses” and in their hemisphere as they move through the night sky.
- The star Ke ali`i o kona i ka lewa (Canopus), rises in Nālani Malanai. Where does it set?
When teaching navigation while sitting on land, it’s perfectly fine to have a rough sketch or model of the star compass. But if you really have to do the navigation, you need to make a very, very precise star compass.
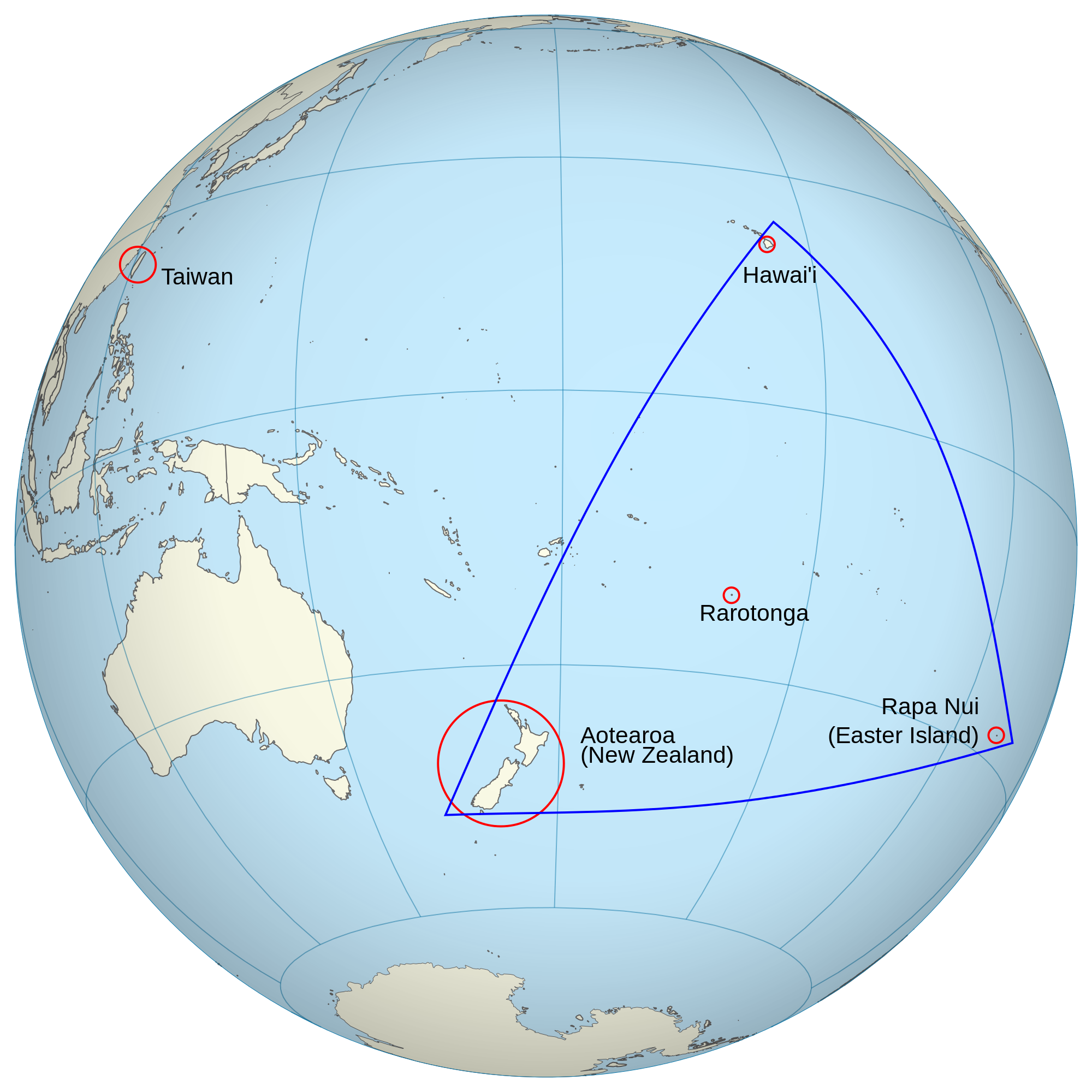
Imagine Nainoa Thompson, who navigated Hōkūle`a on the final leg of her journey from Hawai`i to Rapa Nui, an island even smaller and lower than Ni`ihau. You have to be within 30 miles of Rapa Nui to see it. But a mistake of even one degree would have led to Hōkūle`a being 60 miles off course. And if you end up drifting in the open ocean and supplies run out? Well…

Nainoa Thompson
Now that you have a rough sketch of the star compass and know what it should look like, your job is to draw one that’s as perfect as possible. That means you want to draw:
- A perfect circle (well, as perfect as possible). What tools can you use to do that? What tools would ancient Polynesian navigators have had to use?
- Thirty-two points around the circle that are exactly evenly spaced apart. (What tools would help you? What tools would ancient Polynesian navigators have had to use?)
- When you have finished, label your perfectly drawn star compass with the houses.
Of course, a star compass on a piece of paper isn’t so useful when you’re out on a canoe. How do you position it properly? And how do you keep it from getting lost, damaged, or soaking wet? You paint it on the rails of the canoe, permanently!
Look back at the drawing of Hōkūle`a. Find the “kilo” (navigator’s seat) in the rear (aft) of the canoe. There is actually one navigator’s seat on either side of the deck.
Go back to the scale drawing of Hōkūle`a that you made in Problem 1. Add the navigator’s seats to your drawing. You will then add the star compass to the rails as follows:
- Start with the kilo (seat) on the left (port) side of the canoe. That will be the center of your star compass. Imagine looking to the right. You want to see the star compass markings on the rails when you look to the right. Of course, Hōkūle`a is not a circular canoe, and the navigator doesn’t sit at the center. So how can you make the markings in the right places?
- Now repeat that process, using the seat on the right (starboard) side of the canoe.
|
The kilo onHōkūle`a[4]. |
Compass markings on the rails (to be painted more visibly before voyaging)[5]. |
Nainoa Thompson has said:
Initially, I depended on geometry and analytic mathematics to help me in my quest to navigate the ancient way. However as my ocean time and my time with Mau have grown, I have internalized this knowledge. I rely less on mathematics and come closer and closer to navigating the way the ancients did.
Really he is still doing a lot of mathematics; it’s just mathematics that he has internalized and that is now second nature to him. The ancient navigators may not have spoken of their navigation techniques in the same modern language we’ve been using — compass points and perfect circles and degrees. But their mathematical understanding was truly astonishing.
- Image from pixababy [CC0 Creative Commons]. ↵
- Picture by Maiden Voyage Productions [CC BY-SA 3.0], via Wikimedia Commons ↵
- Image by Newportm (Own work) [CC BY-SA 3.0], via Wikimedia Commons. ↵
- Photo by Michelle Manes. ↵
- Photo by Michelle Manes. ↵




