3.11: Problem Bank
- Page ID
- 10386
Compute the following using dots and boxes:
64212 : 3
44793 : 21
6182 : 11
99916131 : 31
637824 : 302
2125122 : 1011
- Fill in the squares using the digits 4, 5, 6, 7, 8, and 9 exactly one time each to make the largest possible sum: $$\begin{split} \Box\; \Box\; \Box \\ +\; \Box\; \Box\; \Box \\ \hline \end{split}$$
- Fill in the squares using the digits 4, 5, 6, 7, 8, and 9 exactly one time each to make the smallest possible (positive) difference: $$\begin{split} \Box\; \Box\; \Box \\ -\; \Box\; \Box\; \Box \\ \hline \end{split}$$
- Make a base six addition table.
| + | \(0_{six}\) | \(1_{six}\) | \(2_{six}\) | \(3_{six}\) | \(4_{six}\) | \(5_{six}\) |
|---|---|---|---|---|---|---|
| \(0_{six}\) | \(0_{six}\) | \(1_{six}\) | ||||
| \(1_{six}\) | \(10_{six}\) | |||||
| \(2_{six}\) | ||||||
| \(3_{six}\) | ||||||
| \(4_{six}\) | ||||||
| \(5_{six}\) | \(12_{six}\) |
- Use the table to solve these subtraction problems. $$13_{six} - 5_{six} \qquad 12_{six} - 3_{six} \qquad 10_{six} - 4_{six} \ldotp$$
Do these calculations in base four. Don’t translate to base 10 and then calculate there — try to work in base four.
- $$33_{four} + 11_{four}$$
- $$123_{four} + 22_{four}$$
- $$223_{four} - 131_{four}$$
- $$112_{four} - 33_{four}$$
- Make a base five multiplication table.
| \(\times\) | \(0_{five}\) | \(1_{five}\) | \(2_{five}\) | \(3_{five}\) | \(4_{five}\) |
|---|---|---|---|---|---|
| \(0_{five}\) | \(0_{five}\) | \(0_{five}\) | |||
| \(1_{five}\) | |||||
| \(2_{five}\) | |||||
| \(3_{five}\) | \(11_{five}\) | ||||
| \(4_{five}\) | \(22_{five}\) |
- Use the table to solve these subtraction problems. $$11_{five} \div 2_{five} \qquad 22_{five} \div 3_{five} \qquad 13_{five} \div 4_{five} \ldotp$$
- Here is a true fact in base five: $$2_{five} \cdot 3_{five} = 11_{five}$$Write the rest of this four fact family.
- Here is a true fact in base five: $$13_{five} \div 2_{five} = 4_{five}$$Write the rest of this four fact family.
Directions for AlphaMath Problems (Problems 38 – 41):
- Letters stand for digits 0–9.
- In a given problem, the same letter always represents the same digit, and different letters always represent different digits.
- There is no relation between problems (so “A” in part 1 and “A” in part 3 might be different).
- Two, three, and four digit numbers never start with a zero.
- Your job: Figure out what digit each letter stands for, so that the calculation shown is correct.
Notes: In part 2, “O” represents the letter “oh,” not the digit zero.
- $$\begin{split} A & \\ A & \\ +\; A & \\ \hline H\; A & \end{split}$$
- $$\begin{split} O\; N\; E & \\ +\; O\; N\; E & \\ \hline T\; W\; O & \end{split}$$
- $$\begin{split} A\; B\; C & \\ +\; A\; C\; B & \\ \hline C\; B\; A & \end{split}$$
Here’s another AlphaMath problem. \[\begin{split} T\; E\; N & \\ +\; N\; O\; T & \\ \hline N\; I\; N\; E & \end{split} \nonumber \]
- Solve this AlphaMath problem in base 10.
- Now solve it in base 6.
Find all solutions to this AlphaMath problem in base 9.
Notes: Even though this is two calculations, it is a single problem. All T’s in both calculations represent the same digit, all B’s represent the same digit, and so on.
Remember that “O” represents the letter “oh” and not the digit zero, and that two and three digit numbers never start with the digit zero
\[ \begin{split} T\; O & \\ -\; B\; E & \\ \hline O\; R & \end{split} \qquad \begin{split} N\; O\; T & \\ -\; T\; O & \\ \hline B\; E & \end{split} \nonumber \]
This is a single AlphaMath problem. (So all G’s represent the same digit. All A’s represent the same digit. And so on.)
Solve the problem in base 6. \[GALON = (GOO)^{2} \qquad \qquad ALONG = (OOG)^{2} \nonumber \]
A perfect square is a number that can be written as or
(some number times itself).
- Which of the following base seven numbers are perfect squares? For each number, answer yes (it is a perfect square) or no (it is not a perfect square) and give a justification of your answer. $$4_{seven} \qquad 25_{seven} \qquad 51_{seven}$$
- For which choices of base
is the number \(b^{2}\) a perfect square? Justify your answer.
Geoff spilled coffee on his homework. The answers were correct. Can you determine the missing digits and the bases?
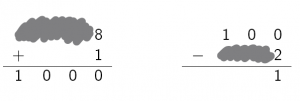
- Rewrite each subtraction problem as an addition problem: $$x - 156 = 279 \qquad 279 - 156 = x \qquad a - x = b \ldotp$$
- Rewrite each division problem as a multiplication problem: $$24 \div x = 12 \qquad x \div 3 = 27 \qquad a \div b = x \ldotp$$
Which of the following models represent the same multiplication problem? Explain your answer.
Show an area model for each of these multiplication problems. Write down the standard computation next to the area model and see how it compares. \[20 \times 33 \qquad 24 \times 13 \qquad 17 \times 11 \nonumber \]
Suppose the 2 key on your calculator is broken. How could you still use the calculator compute these products? Think about what properties of multiplication might be helpful. (Write out the calculation you would do on the calculator, not just the answer.) \[1592 \times 3344 \qquad 2008 \times 999 \qquad 655 \times 525 \nonumber \]
Today is Jennifer’s birthday, and she’s twice as old as her brother. When will she be twice as old as him again? Choose the best answer and justify your choice.
- Jennifer will always be twice as old as her brother.
- It will happen every two years.
- It depends on Jennifer’s age.
- It will happen when Jennifer is twice as old as she is now.
- It will never happen again.
- Find the quotient and remainder for each problem. $$7 \div 3 \qquad 3 \div 7 \qquad 7 \div 1 \qquad 1 \div 7$$
- How many possible remainders are there when dividing by these numbers? Justify what you say. $$2 \qquad 12 \qquad 62 \qquad 23$$
Identify each problem as either partitive or quotative division and say why you made that choice. Then solve the problem.
- Adriana bought 12 gallons of paint. If each room requires three gallons of paint, how many rooms can she paint?
- Chris baked 15 muffins for his family of five. How many muffins does each person get?
- Prof. Davidson gave three straws to each student for an activity. She used 51 straws. How many students are in her class?
Use the digits 1 through 9. Use each digit exactly once. Fill in the squares to make all of the equations true. \[\begin{split} \Box - \Box = \Box & \\ \times & \\ \Box \div \Box = \Box & \\ = & \\ \Box + \Box = \Box & \end{split} \nonumber \]