4.7: Dividing Fractions- Meaning
- Page ID
- 10579
Dividing fractions is one of the hardest ideas in elementary school mathematics. By now, you are used to the rule: to divide by a fraction, multiply by its reciprocal. (“invert and multiply”). But ask yourself: Why does this rule work? Does it really make sense to you? Can you explain why it makes sense to a third grader?
We are going to build up to the “invert and multiply” rule, but along the way, we’ll find some more meaningful ways to understand division of fractions. So please play along: pretend that you don’t already know the “invert and multiply” rule, and solve the problems in this chapter with other methods.
Groups of Equal Size
Remember the quotative model for division: \(18 \div 3\) means:
How many groups of 3 can I find in 18?
We start with 18 dots (or candy bars or molecules), and we make groups of 3 dots (or 3 whatevers). We ask: how many groups can we make?
18 dots, split into groups of 3 dots. Since there are 6 groups, we have 18 : 3 = 6.
This same idea applies when we divide fractions. For example, \(6 \div 23\) means:
How many groups of \(\frac{2}{3}\) can I find in 6?
Let’s draw a picture of 6 pies, and see how many groups of \(\frac{2}{3}\) we can find:
We found nine equal groups of size \(\frac{2}{3}\), so we conclude that \[6 \div \frac{2}{3} = 9 \ldotp \nonumber \]
Unfortunately, it’s not always quite so straightforward to find the equal groups. For example, \(\frac{3}{4} \div \frac{1}{3}\) asks the question:
How many groups of \(\frac{1}{3}\) can I find in \(\frac{3}{4}\)?
Let’s draw a picture of \(\frac{3}{4}\) of a pie, and see how many groups of \(\frac{1}{3}\) we can find:
The first pictures shows \(\frac{3}{4}\) of a pie. The second picture shows two equal groups of \(\frac{1}{3}\) inside of \(\frac{3}{4}\), but there’s a little bit left over. We conclude $$\frac{3}{4} \div \frac{1}{3} = 2 + \text{a tiny bit more} \ldotp$$But how much more? Can we figure it out exactly?
Here’s a method that will let you do the computation exactly. We’ll use rectangular pies, and divide them up into rows and columns based on the denominators of the numbers we’re dividing.
Start by drawing two identical rectangles, each with 4 rows (from the denominator of \(\frac{3}{4}\) and 3 columns (from the denominator of \(\frac{1}{3}\)).
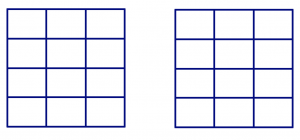
Shade \(\frac{3}{4}\) of the first rectangle (this is exactly three rows), and shade \(\frac{1}{3}\) of the second rectangle (so that’s one column).
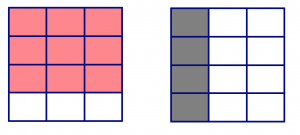
Now ask: how many copies of \(\frac{1}{3}\) can I find in \(\frac{3}{4}\)? Well, \(\frac{1}{3}\) is equal to four of the smaller squares. So we find groups equal to that:
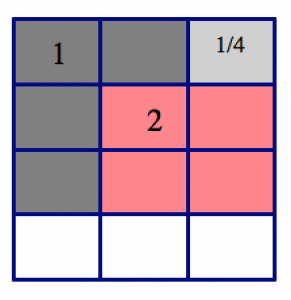
In the picture of \(\frac{3}{4}\), we can find:
- two groups of four squares (two groups of \(\frac{1}{3}\)), and
- one square left over, which is \(\frac{1}{4}\) of the group we’re looking for.
We conclude: \[\frac{3}{4} \div \frac{1}{3} = 2 \frac{1}{4} \ldotp \nonumber \]
Use either method above to find the following quotients. Remember, pretend that you don’t know any method to divide fractions except finding equal-sized groups.
\[\frac{3}{4} \div \frac{1}{2} \qquad \frac{1}{3} \div \frac{1}{2} \qquad \frac{4}{9} \div \frac{1}{3} \qquad \frac{4}{5} \div \frac{1}{3} \qquad \frac{3}{5} \div \frac{3}{4} \qquad \frac{3}{2} \div \frac{1}{2} \qquad \frac{2}{3} \div \frac{1}{2} \nonumber \]
Common Denominator Method
Solve each of the following fraction division problems using the “groups of equal size” method: $$\frac{6}{4} \div \frac{3}{4} \qquad \frac{6}{10} \div \frac{3}{10} \qquad \frac{8}{9} \div \frac{4}{9} \qquad \frac{6}{33} \div \frac{2}{33} \qquad \frac{5}{4} \div \frac{2}{4} \qquad \frac{5}{2} \div \frac{2}{2} \qquad \frac{5}{10} \div \frac{2}{10}$$What do you notice?
This leads to our first fraction division method:
If two fractions have the same denominator, then when you divide them, you can just divide the numerators. In symbols, \[\frac{a}{d} \div \frac{b}{d} = \frac{a}{b} \ldotp \nonumber \]
- Use the common denominator method to find these quotients: $$\frac{1}{3} \div \frac{2}{3}, \qquad \frac{5}{8} \div \frac{3}{8}, \qquad \frac{3}{8} \div \frac{5}{8}, \qquad \frac{15}{33} \div \frac{1}{33},$$
- What if the fractions do not have a common denominator? Is the method useless, or can you find a way to make it work? Can you solve these problems?$$\frac{3}{5} \div \frac{3}{4}, \qquad \frac{3}{4} \div \frac{8}{7}, \qquad \frac{2}{3} \div \frac{1}{2}, \qquad \frac{5}{8} \div \frac{1}{4} \ldotp$$
Missing Factor Method
We know that we can always turn a division problem into a “missing factor” multiplication problem. Can that help us compute fraction division? Sometimes!
For each division problem, rewrite it as a missing factor multiplication question. Then find the quotient using what you know about multiplying fractions.
\[\frac{9}{10} \div \frac{3}{5}, \qquad \frac{7}{8} \div \frac{1}{4}, \qquad \frac{6}{7} \div \frac{3}{7}, \qquad \frac{10}{9} \div \frac{2}{3}, \qquad \frac{25}{12} \div \frac{5}{6} \ldotp \nonumber \]
Unfortunately, the missing factor method doesn’t always work out so nicely. For example,
\[\frac{3}{4} \div \frac{1}{3} = \_\_ \nonumber \]
can be rewritten as
\[\frac{1}{3} \cdot \_\_ = \frac{3}{4} \ldotp \nonumber \]
There isn’t a nice ratio of whole numbers that obviously fills in the blank, but we’ll come back to this idea and resolve it soon.


