5.5: Matching Game
- Page ID
- 9853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Below, you’ll find patterns described in various ways: through visual representations, algebraic expressions, in tables of numbers, and in words. Your job is to match these up in a way that makes sense.
Note: there may be more than one algebraic expression to match a given pattern, or more than one pattern to match a given description. So be ready to justify your answers.
Algebraic Expressions
| (a) \(t^{2}\) | (b) \(2s + 1\) | (c) \(2k + (k - 1) + 2k + (k - 1)\) |
| (d) \(5n + 5\) | (e) \(a + a\) | (f) \(3(\ell - 1) + 3(\ell -1)+4\) |
| (g) \(3b + 1\) | (h) \(z+z+1\) | (i) \(m^{2} - (m-1)^{2}\) |
| (j) \(y \cdot y\) | (k) \(2x - 1\) | (l) \(4e - (e-1)\) |
| (m) \(6f -2\) | (n) \(2xc\) | (o) \(5(s+1)\) |
Visual Patterns
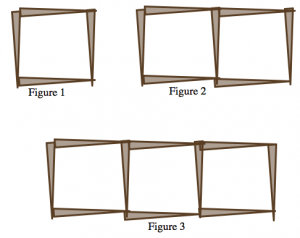
Pattern 1
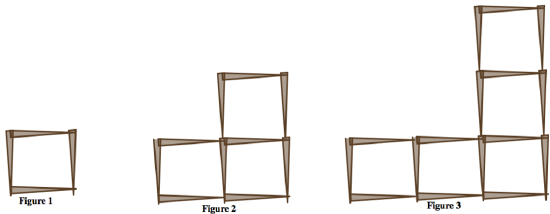
Pattern 2
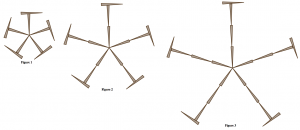
Pattern 3
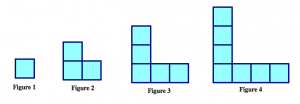
Pattern 4

Pattern 5

Pattern 6

Pattern 7
Tables of Numbers
| Table A | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 1 | 4 | 9 | 16 |
| Table B | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 10 | 15 | 20 | 25 |
| Table C | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 1 | 3 | 5 | 7 |
| Table D | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 3 | 5 | 7 | 9 |
| Table E | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 4 | 7 | 10 | 13 |
| Table F | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 4 | 10 | 16 | 22 |
| Table G | ||||
|---|---|---|---|---|
| Input | 1 | 2 | 3 | 4 |
| Output | 2 | 4 | 6 | 8 |
Descriptions in Words
- Count horizontal and vertical toothpicks separately. Horizontal: there are two rows of n toothpicks where n is the figure number. There are \(n-1\) more of them on the vertical arm. The vertical toothpicks are just the same. There are two columns of n along the vertical arm, and then n-1 more of them on the horizontal arm.
- To get a figure from the previous one, you add three toothpicks in a “C”’ shape on the left side of the figure. The total number of toothpicks is three times the figure number, plus one extra to close off the square on the far right.
- There are five spikes radiating out from the center. Each spike has the same number of toothpicks as the figure number. Each spike is capped off by one additional toothpick.
- Each arm of the “L” shape has the same number of tiles as the figure number. But then we’ve counted the corner of the “L” twice, so we have to subtract one to get the total number of tiles needed.
- The stars are in two equal rows, and each row has the same number of stars as the figure number.
- To make the next figure, you always add five more toothpicks. Each arm has one more than the figure number of toothpicks, and there are five arms.
- The stars are in a square, and the sides of the square have the same number of stars as the figure number.
- Each arm of the “V” shape has the same number of stars as the figure number. Then we need to add one more star for the corner.
- There are the same number of squares as the figure number, and each square uses four toothpicks. But then I’ve double-counted the toothpicks where the squares touch, so we have to subtract those out. There are one less of those than the figure number.
- I can picture a square of tiles filled in. The side length of that square is the same as the figure number, so that’s \(x^{2}\). But then the square isn’t really filled in. It’s like I took away a square one size smaller from the top right, leaving just the border. What I took away was a square one size smaller, \((x-1)^{2}\).
- Each time I go from one shape to the next, I add six new toothpicks. Three are added to the left in a “C” shape and three are added to the top in a rotated “C”’ shape. So the total number will be six times the figure number plus or minus something. I can check to see that the right correction is to subtract 2.


