5.7: Problem Bank
- Page ID
- 10654
Problems 34-36 ask you to solve problems about a strange veterinarian who created three mystifying machines.
Cat Machine: Place a cat in the input bin of this machine, press the button, and out jump two dogs and a mouse.
Dog Machine: This machine converts a dog into a cat and a mouse.
Mouse Machine: This machine can convert a mouse into a cat and three dogs.
Each machine can also operate in reverse. For example, if you have two dogs and a mouse, you can use the first machine to convert them into a cat.
The veterinarian hands you two cats, and asks you to convert them into exactly three dogs (no extra dogs and no other animals). Can you do it? If yes, say what process you would use. If no, say why not.
The veterinarian hands you one dog. He says he only wants cats, but he doesn’t care how many. Can you help him? How?
The veterinarian hands you one cat. He says he only wants dogs, but he doesn’t care how many. Can you help him? How?
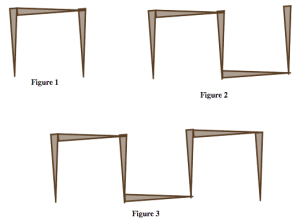
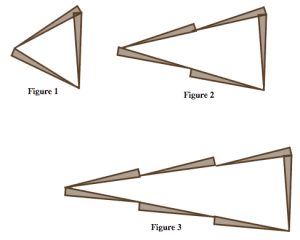
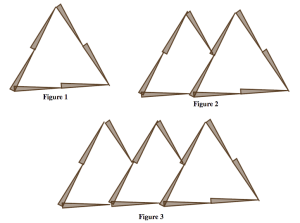
Problems 37-40 present several growing patterns made with toothpicks. For each problem you work on, do the following:
- Describe in words and pictures how you see the pattern growing.
- Calculate the number of toothpicks you would need to build the 10th figure in the pattern. Justify your answer based on how the pattern grows.
- Calculate the number of toothpicks you would need to build the 100th figure in the pattern.
- Describe how you can figure out the number of toothpicks in any figure in the pattern. Be sure to justify your answer based on how the pattern grows.
- Could you make one of the figures in the pattern using exactly 25 toothpicks? If yes, which figure? If no, why not? Justify your answer.
- Could you make one of the figures in the pattern using exactly 100 toothpicks? If yes, which figure? If no, why not? Justify your answer.
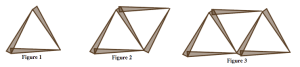
In a mobile, the arms must be perfectly balanced for it to hang properly. The artist Alexander Calder was famous for his artistic mobiles.You can view some of his amazing work here. Click “Explore Works.”
Problems 41-42 present you with mobile puzzles. In these puzzles:
- Objects that are the same shape have the same weight. (So all circles weigh the same, all squares weigh the same, etc.)
- Assume the strings and rods that hold the objects together don’t factor into the total weight.
- Each arm of the mobile must have exactly the same weight.
In this puzzle:
- The total weight is 36 grams.
- All shapes weigh less than 10 grams.
- All of the weights are whole numbers.
- One circle weighs more than one square.
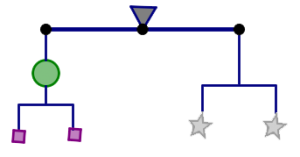
Find the weight of each piece. Is there more than one answer? How do you know you are right?
In this puzzle, the total weight is 54 grams.
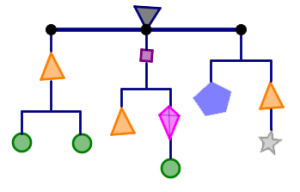
Find the weight of each piece. Is there more than one answer? How do you know you are right?


