6.1: Review of Dots and Boxes Model
- Page ID
- 9856
Let’s start with a quick review of place value, different bases, and our “Dots & Boxes” model for thinking about these ideas.
Whenever there are two dots in single box, they “explode,” disappear, and become one dot in the box to the left.
We start by placing nine dots in the rightmost box.
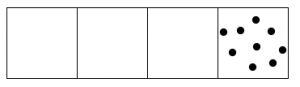
Two dots in that box explode and become one dot in the box to the left.

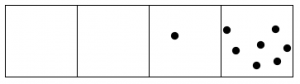
Once again, two dots in that box explode and become one dot in the box to the left.
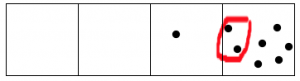
We do it again!
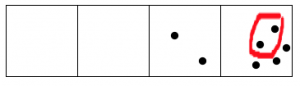
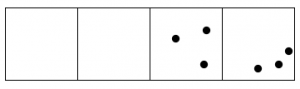
Hey, now we have more than two dots in the second box, so those can explode and move!
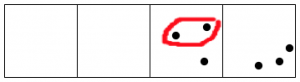
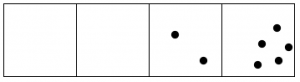
And the rightmost box still has more than two dots.
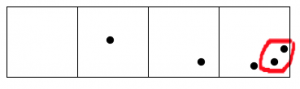
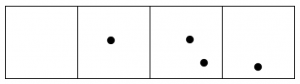
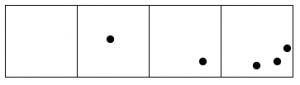
Keep going, until no box has two dots.
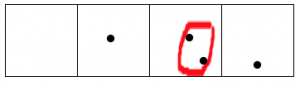
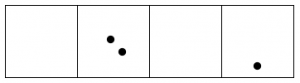
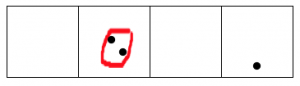
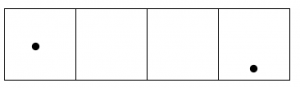
After all this, reading from left to right we are left with one dot, followed by zero dots, zero dots, and one final dot.
- Answer
-
The 2←1 code for nine dots is: 1001.
Whenever there are three dots in single box, they “explode,” disappear, and become one dot in the box to the left.
Here’s what happens with fifteen dots:
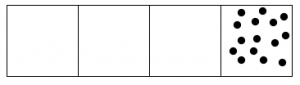
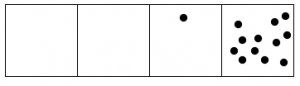
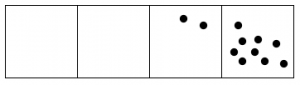
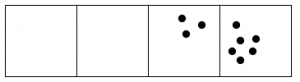
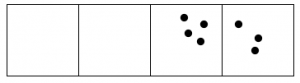
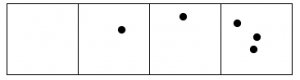
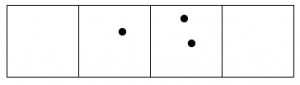
- Answer
-
The 1←3 code for fifteen dots is: 120.
Recall that numbers written in the 1←2 system are called binary or base two numbers.
Numbers written in the 1←3 system are called base three numbers.
Numbers written in the 1←4 system are called base four numbers.
Numbers written in the 1←10 system are called base ten numbers.
In general, numbers written in the 1←b system are called base b numbers.
In a base b number system, each place represents a power of b, which means \(b^{n}\) for some whole number n. Remember this means b multiplied by itself n times:
- The right-most place is the units or ones place. (Why is this a power of b?)
- The second spot is the “b” place. (In base ten, it’s the tens place.)
- The third spot is the “\(b^{2}\)” place. (In base ten, that’s the hundreds place. Note that \(10^{2} = 100\).)
- The fourth spot is the “\(b^{3}\)” place. (In base ten, that’s the thousands place, since \(10^{3} = 1000\).)
- And so on.
Whenever we’re dealing with numbers written in different bases, we use a subscript to indicate the base so that there can be no confusion. So:
- \(102_{three}\) is a base three number (read it as “one-zero-two base three”). This is the base three code for the number eleven.
- \(222_{four}\) is a base four number (read it as “two-two-two base four”). This is the base four code for the number forty-two.
- \(54321_{ten}\) is a base ten number. (It’s ok to say “fifty-four thousand three hundred and twenty-one.” Why?)
If the base is not written, we assume it’s base ten.
Remember: when you see the subscript, you are seeing the code for some number of dots.
Work through the two examples above carefully to be sure you remember and understand how the “Dots & Boxes” model works. Then answer these questions:
- When we write 9 in base 2, why do we write \(1001_{two}\) instead of just \(11_{two}\)?
- When we write 15 in base 3, why do we write \(120_{three}\) instead of just \(12_{three}\)?
- How many different digits do you need in a base 7 system? In a base 12 system? In a base b system? How do you know?
On Your Own
Work on the following exercises on your own or with a partner.
- In base 4, four dots in one box are worth one dot in the box one place to the left.
- What is the value of each box?
- How do you write \(29_{ten}\) in base 4?
- How do you write \(132_{four}\) in base 10?
- In our familiar base ten system, ten dots in one box are worth one dot in the box one place to the left.
- What is the value of each box?
- When we write the base ten number 7842:
- What quantity does the “7” represent?
- The “4” is four groups of what value?
- The “8” is eight groups of what value?
- The “2” is two groups of what value?
- Write the following numbers of dots in base two, base three, base five, and base eight. Draw the “Dots & Boxes” model if it helps you remember how to do this! (Note: these numbers are all written in base ten. When we don’t say otherwise, you should assume base ten.) $$(a)\; 2 \qquad (b)\; 17 \qquad (c)\; 27 \qquad (d)\; 63 \ldotp$$
- Convert these numbers to our more familiar base ten system. Draw out dots and boxes and “unexplode” the dots if it helps you remember. $$(a)\; 1101_{two} \qquad (b)\; 102_{three} \qquad (c)\; 24_{five} \qquad (d)\; 24_{nine} \ldotp$$
Quickly compute each of the following. Write your answer in the same base as the problem.
- \(131_{ten}\) times ten.
- \(263207_{eight}\) times eight.
- \(563872_{nine}\) times nine.
- Use the 1←10 system to explain why multiplying a whole number in base ten by ten results in simply appending a zero to the right end of the number.
- Suppose you have a whole number written in base b. What is the effect of multiplying that number by b? Justify what you say.


