6.5: More x -mals
- Page ID
- 9860
It should come as no surprise that we can use this reasoning about division in the “Dots & Boxes” model in other bases as well.
The following picture shows that working in base 5,
\[1432_{five} \div 13_{five} = 110_{five} R2_{five},\; \text{meaning}\; 1432_{five} = 110_{five} \cdot 13_{five} + 2_{five} \ldotp \nonumber \]
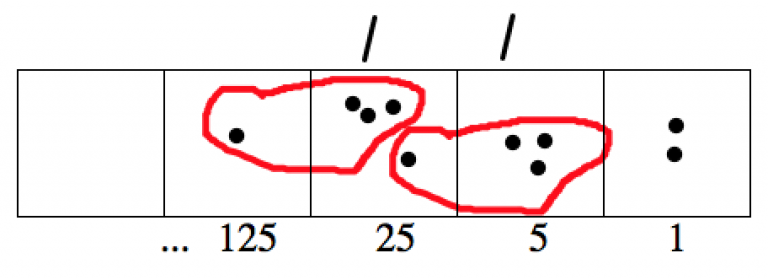
Carefully explain the connection between the picture and the equation shown above.
- Show in the picture where you see \(1432_{five}\) from the equation.
- Where do you see \(13_{five}\)?
- Where do you see \(110_{five}\) and \(2_{five}\)?
Here’s where we left off the division, with a remainder of 2:
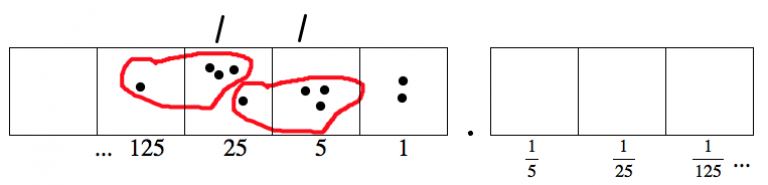
Now we can unexplode one of those two remaining dots. Then we’re able to make another group of \(13_{five}\).
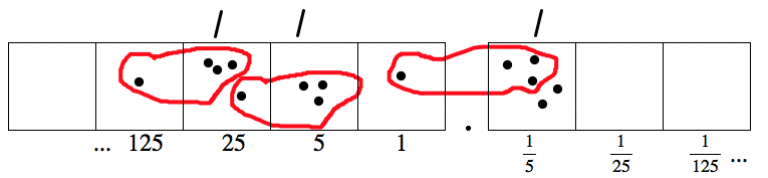
Once again, there are two dots left over, not in any group. So let’s unexplode one of them.
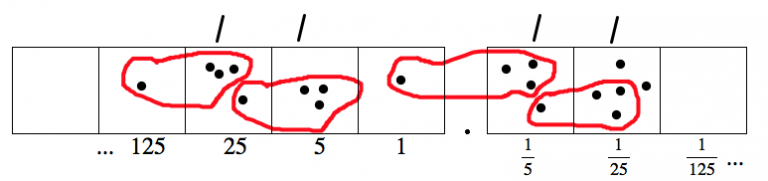
And we still have two dots left over. Why not do it again?
It seems like we’re going to be doing the same thing forever:
- Start with two dots in some box.
- Unexplode one one of the dots, so you have one dot in your original box and five in the box to the right.
- Form a group of \(3_{five}\). That uses the one dot in your original box and three dots in the box to the right.
- So you have two dots left in a box.
- Unexplode one of the dots, so you have one dot in your original box and five in the box to the right.
- This feels familiar…
We conclude:
\[1432_{five} \div 13_{five} = 110.111 \ldots_{five} = 110. \bar{1}_{five} \ldotp \nonumber \]
The equation
\[1432_{five} \div 13_{five} = 110. \bar{1}_{five} \ldotp \nonumber \]
is a statement in base five. What is it saying in base ten?
“\(1432_{five}\)” is the number
\[1 \cdot 125 + 4 \cdot 25 + 3 \cdot 5 + 2 \cdot 1 = 242_{ten} \ldotp \nonumber \]
- What is \(13_{five}\) in base 10? Be sure to explain your answer.
- What is \(110. \bar{1}_{five}\) in base 10? Explain how you got your answer.
- Translate the equation above to a statement in base ten and check that it is correct.
- Draw pictures to compute \(8 \div 3\) in a base ten system, and show the answer is \(2. \bar{6}\).
- Draw the pictures to compute \(8_{nine} \div 3_{nine}\) in a base 9 system, and write the answer as a decimal. (Or is it a “nonimal”?)
- Draw the pictures to compute \(1 \div 11\) in a base ten system, and show the answer is \(0. \overline{09}\).
- Draw the base 3 pictures to compute \(1_{three} \div 11_{three}\), and write the answer as a decimal (“trimal”?) number.
- Draw the base four pictures to compute \(1_{four} \div 11_{four}\), and write the answer as a decimal (“quadimal”?) number.
- Draw the base six pictures to compute \(1_{six} \div 11_{six}\), and write the answer as a decimal (“heximal”?) number.
- Describe any patterns you notice in the computations above. Do you have a conjecture of a general rule? Can you prove your general rule is true?
Remember that the fraction \(\frac{2}{5}\) represents the division problem \(2 \div 5\). (This is all written in base ten.)
- What is the decimal expansion (in base ten) of the fraction \(\frac{2}{5}\)?
- Rewrite the base-ten fraction \(\frac{2}{5}\) as a base four division problem. Then find the decimal expansion for that fraction in base four.
- Rewrite the base-ten fraction \(\frac{2}{5}\) as a base five division problem. Then find the decimal expansion for that fraction in base five.
- Rewrite the base-ten fraction \(\frac{2}{5}\) as a base seven division problem. Then find the decimal expansion for that fraction in base seven.
- Barry said that in base fifteen, the division problem looks like $$2_{fifteen} \div 5_{fifteen},$$and the decimal representation would be \(0.6_{fifteen}\). Check Barry’s answer. Is he right?
Expand each of the following as a “decimal” number in the base given. (The fraction is given in base ten.)
\[\begin{split} (a)\; \frac{1}{9}\; \text{in base 10} \quad \qquad &(b)\; \frac{1}{2}\; \text{in base 3} \\ (c)\; \frac{1}{3}\; \text{in base 4} \quad \qquad &(d)\; \frac{1}{4}\; \text{in base 5} \\ (e)\; \frac{1}{5}\; \text{in base 6} \quad \qquad &(f)\; \frac{1}{6}\; \text{in base 7} \\ (g)\; \frac{1}{7}\; \text{in base 8} \quad \qquad &(h)\; \frac{1}{8}\; \text{in base 9} \end{split} \nonumber \]
Do you notice any patterns? Any conjectures?
What fraction has decimal expansion \(0. \bar{3}_{seven}\)? How do you know you are right?


