9.4: Equivalent Payments
- Page ID
- 22120
Unforeseen events and circumstances can force you to rearrange your financial commitments. When this happens, the new deal has to be fair to all parties concerned.
Suppose you and your co-workers rely on your company’s annual Christmas bonuses. However, the CEO just announced that because of tough economic conditions no one will get a bonus this year. You already earmarked that money to pay a $5,000 debt due next week. You want to be financially responsible, but you cannot possibly make the payment. Before picking up the phone to call your creditor, you need to determine what course of action you should pursue.
You need to make alternative arrangements that leave your creditor in the same financial position as the original agreement did. You saw in the previous section that if you were going to make an early payment, the payment should be reduced by an agreed-upon discount rate. In this case, though, you are going to make a late payment, so you must grant the creditor interest. Thus, if you propose paying the debt six months late and your creditor agrees to 9% compounded monthly as a fair rate, then you owe $5,229.26 (applying Formula 9.3).
This concept applies to all aspects of your personal and professional life. Except for gifts, personal debts to friends or family members should bear some interest. Everyone should be financially fair to each other. A business must be willing to work with its clients in the event they need to alter an agreement. A company that is inflexible tends to find itself writing off bad debt or pursuing unpleasant and sometimes expensive legal action.
This section explores the concept of equivalent payment streams. This involves equating two or more alternative financial streams to ensure that neither party is penalized by any choice. You then apply the concept of present value to loans and loan payments.
Fundamental Concepts
The Fundamental Concept of Time Value of Money
All numbers in an equation must be expressed in the same units, such as kilometers or meters. In the case of money, you treat the time at which you are considering the value as the “unit” that needs to be the same. Because of interest, a dollar today is not the same as a dollar a year ago or a dollar a year from now, so you cannot mix dollars from different times within the same equation; you must bring all monies forward or back to a common point in time, called the focal date.
The fundamental concept of time value of money states that all monies must be brought to the same focal date before any mathematical operations, decisions, or equivalencies can be determined, including the following:
- Simple mathematics such as addition or subtraction.
- Deciding whether to adopt alternative financial agreements.
- Determining if payment streams are equal.
The Fundamental Concept of Equivalency
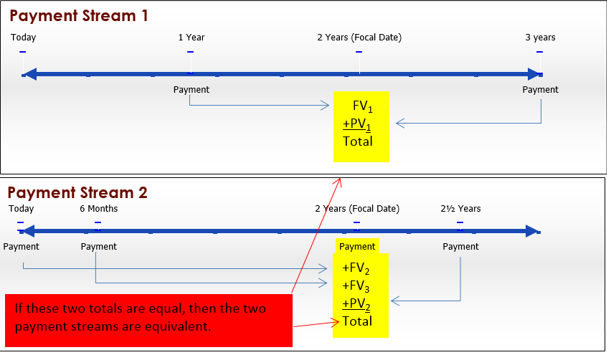
The fundamental concept of equivalency states that two or more payment streams are equal to each other if they have the same economic value on the same focal date. As illustrated in the figure, the two alternative financial streams are equivalent if the total of Payment Stream 1 is equal to the total of Payment Stream 2 on the same focal date. Note that the monies involved in each payment stream can be summed on the focal date because of the fundamental concept of time value of money.
Equivalent Payments
You make alternative payment streams equivalent to each other by applying a prevailing interest rate that allows for the following:
- Any late payments to be charged interest through future value calculations (Section 9.2)
- Any early payments to have interest deducted through present value calculations (Section 9.3)
The Formula
The good news is that you need no new formulas. Depending on the structure of the payment streams needing to be equated, apply Formula 9.3 as is or rearrange the formula for \(PV\). As illustrated in the previous figure, Payment Stream 1 involves calculating one future value and one present value to move the money to the focal date. Payment Stream 2 involves calculating two future values and one present value. Once all money is moved to the same focal date, you work with the equality between the values of the two payment streams, solving for any unknown variable or variables.
How It Works
Follow these steps to solve an equivalent payment question:
Step 1: Draw as many timelines as needed to illustrate each of the original and proposed agreements. Clearly indicate dates, payment amounts, and the interest rate(s).
Step 2: Choose a focal date to which all money will be moved.
Step 3: Calculate all needed periodic interest rates using Formula 9.1.
Step 4: Calculate N for each payment using Formula 9.2.
Step 5: Perform the appropriate time value calculation using Formula 9.3.
Step 6: Equate the values of the original and proposed agreements on the focal date and solve for any unknowns.
Assume you owe $1,000 today and $1,000 one year from now. You find yourself unable to make that payment today, so you indicate to your creditor that you want to make both payments six months from now instead. Prevailing interest rates are at 6% compounded semi-annually. What single payment six months from now (the proposed payment stream) is equivalent to the two payments (the original payment stream)?
Step 1: The timeline illustrates the scenario.
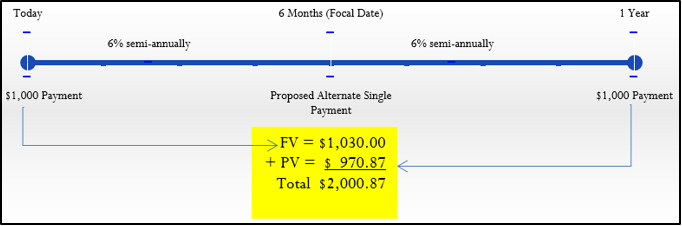
Step 2: Apply the fundamental concept of time value of money, moving all of the money to the same date. Since the proposed payment is for six months from now, you choose a focal date of six months.
Step 3: Note that semi-annual compounding means \(CY\) = 2. From Formula 9.1, \(I=6 \% / 2=3 \%\).
Step 4: Formula 9.2 produces \(N=2 \times \dfrac{1}{2}=1\) compound for both payments (each moving a \(\dfrac{1}{2}\) year).
Step 5: Moving today’s payment of $1,000 six months into the future, you have \(FV=\$ 1,000(1+0.03)^{1}=\$ 1,030.00\). Moving the future payment of $1,000 six months earlier, you have \(\$ 1,000=PV(1+0.03)^{1} \text { or } PV=\$ 970.87\).
Step 6: Now that money has been moved to the same date you can sum the two totals to determine the equivalent payment, which is \(\$ 1,030.00+\$ 970.87=\$ 2,000.87\). Note that this is financially fair to both parties. For making your $1,000 payment six months late, the creditor is charging you $30 of interest. Also, for making your second $1,000 payment six months early, you are receiving a benefit of $29.13. This leaves both parties compensated equitably: Neither party is financially better or worse off because of the change in the deal.
Paths To Success
When you make two (or more) payment streams equal to each other, two tips will make the procedure easier:
- Proper Timelines Timelines help you see what to do. If you draw two or more timelines, align them vertically, ensuring that all corresponding dates are in the same columns. This allows you to see which payments need to be future valued and which need to be present valued to express them in terms of the chosen focal date.
- Locate the Focal Date at an Unknown In one sense, it does not matter what focal date you choose because two values that are equal when moved to one date in common will still be equal when both are moved together to another date. But you should simplify your calculations by selecting a focal date corresponding to the date of an unknown variable. Then when you calculate the root of the equation, it will already be in the right amount on the right date. You will not require further calculations to move the money to its correct date. For example, in the scenario above you had to determine the amount of a payment that was to be made six months from now. By setting the focal date at six months—the date of the unknown you were trying to find—you avoided any extra conversions.
Johnson’s Garden Centre has recently been unprofitable and concludes that it cannot make two debt payments of $4,500 due today and another $6,300 due in three months. After discussions between Johnson’s Garden Centre and its creditor, the two parties agree that both payments could be made nine months from today, with interest at 8.5% compounded monthly. What total payment does Johnson’s Garden Centre need nine months from now to clear its debt?
Solution
Calculate and sum the future value of each of the missed payments at the nine-month point with interest, or \(FV\) for both.
What You Already Know
Step 1:
The amount of the missed payments, interest rate, and term are illustrated on the timeline.
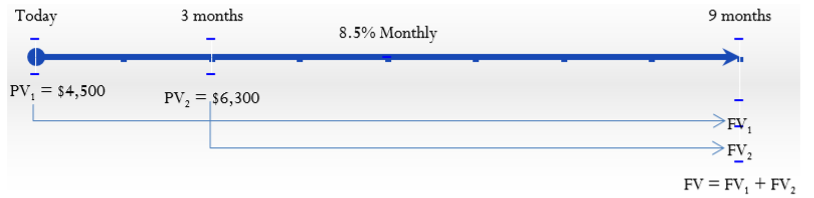
\(PV_1\) (today) = $4,500; \(PV_2\) (3 months from now) = $6,300; \(IY\) = 8.5%; \(CY\) = 12
Step 2:
Due date for all = 9 months from today. This is your focal date.
How You Will Get There
Step 3:
Calculate the periodic interest rate by applying Formula 9.1.
Step 4:
For each payment, calculate the number of compound periods (\(N\)) by applying Formula 9.2.
Step 5:
For each payment, calculate the maturity value (\(FV_1\) and \(FV_2\) by applying Formula 9.3.
Step 6:
Calculate the total payment by summing the two payments, (\(FV_1\) and \(FV_2\), together.
Perform
Step 3:
\[i=\dfrac{8.5 \%}{12}=0.708 \overline{3} \%=0.00708 \overline{3} \nonumber \]
Step 4:
The first payment moves nine months into the future, or 9/12 of a year. \(N\) = 12 × 9/12 = 9.
The second payment moves six months into the future, or 6/12 of a year. \(N\) = 12 × 6/12 = 6.
Step 5:
First payment: \(FV_{1}=\$ 4,500(1+0.00708 \overline{3})^{9}=\$ 4,795.138902\)
Second payment: \(FV_{2}=\$ 6,300(1+0.00708 \overline{3})^{6}=\$ 6,572.536425\)
Step 6:
\[FV=\$ 4,795.138902+\$ 6,572.536425=\$ 11,367.68 \nonumber \]
Calculator Instructions
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 9 | 8.5 | 4500 | 0 | Answer: -$ 4,795.138902 | 12 | 12 |
| 2 | 6 | \(\surd\) | 6300 | \(\surd\) | Answer: -$ 6,572.526425 | \(\surd\) | \(\surd\) |
With interest, the two payments total $11,367.68. This is the $10,800 of the original principal plus $567.68 in interest for making the late payments.
You have three debts to the same creditor: $3,000 due today, $2,500 due in 2¼ years, and $4,250 due in 3 years 11 months. Unable to fulfill this obligation, you arrange with your creditor to make two alternative payments: $3,500 in nine months and a second payment due in two years. You agree upon an interest rate of 9.84% compounded monthly. What is the amount of the second payment?
Solution
Determine the amount of the second payment that is due two years from today. Apply the fundamental concept of time value of money, moving all money from the original and proposed payment streams to a focal date positioned at the unknown payment. Once all money is moved to this focal date, apply the fundamental concept of equivalence, solving for the unknown payment, or \(x\).
What You Already Know
Step 1:
With two payment streams and multiple amounts all on different dates, visualize two timelines. The payment amounts, interest rate, and due dates for both payment streams are known.
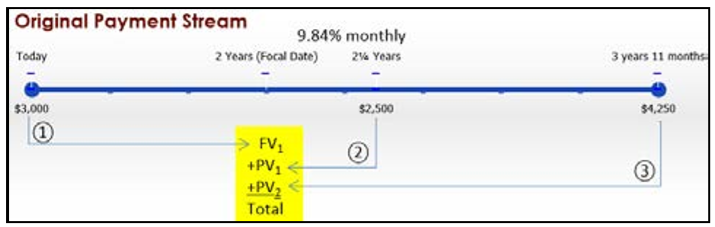
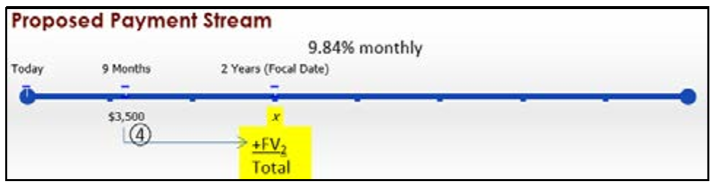
\(IY\) = 9.84%; \(CY\) = monthly = 12
How You Will Get There
Step 2:
A focal date of Year 2 has been selected.
Step 3:
Calculate the periodic interest rate by applying Formula 9.1.
Step 4:
For each payment, calculate the number of compound periods by applying Formula 9.2.
Step 5:
For each payment, apply Formula 9.3. Note that all payments before the two year focal date require you to calculate future values, while all payments after the two-year focal date require you to calculate present values.
Step 6:
Set the value of the original payment stream equal to the proposed payment stream. Solve for the unknown payment, \(x\), using algebra.
\(FV_{1}+PV_{1}+PV_{2}=x+FV_{2}\)
Perform
Step 3:
\[i=\dfrac{9.84 \%}{12}=0.82 \% \text { or } 0.0082 \nonumber \]
Steps 4 and 5:
Using the circled number references from the timelines:
① \(N = 12 × 2 = 24\); \(FV_1 = \$3,000(1 + 0.0082)^{24} = \$3,649.571607\)
② \(N= 12 × ¼ = 3\); \(\$2,500 = PV_1(1 + 0.0082)^3\); \(PV_{1}=\dfrac{\$ 2,500}{1.0082^{3}}=\$ 2,439.494983\)
③ \(N=12 \times 1 \tfrac{11}{12}=23\); \(\$ 4,250=PV_{2}(1+0.0082)^{23}\); \(PV_{2}=\dfrac{\$ 4,250}{1.0082^{23}}=\$ 3,522.207915\)
④ \(N=12 \times 1\tfrac{1}{4}=15\); \(FV_{2}=\$ 3,500(1+0.0082)^{15}=\$ 3,956.110749\)
Step 6:
\[\begin{aligned}
\$ 3,649.571607+\$ 2,439.494983+\$ 3,522.207915 &=x+\$ 3,956.110749 \\
\$ 9,611.274505 &=x+\$ 3,956.110749 \\
\$ 5,655.16 &=x
\end{aligned} \nonumber \]
Calculator Instructions
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| ① | 24 | 9.84 | 3000 | 0 | Answer: -$ 3,649.571607 | 12 | 12 |
| ② | 3 | \(\surd\) | Answer: -$ 2,439.494983 | \(\surd\) | 2500 | \(\surd\) | \(\surd\) |
| ③ | 23 | \(\surd\) | Answer: -$ 3,522.207915 | \(\surd\) | 4250 | \(\surd\) | \(\surd\) |
| ④ | 15 | \(\surd\) | 3500 | \(\surd\) | Answer: -$ 3,956.110749 | \(\surd\) | \(\surd\) |
The second payment is $5,655.16. This makes the original and proposed agreements equivalent to each other.

Working with Loans and Payments
The fundamental concepts of time value of money and equivalency will help you understand better how loans operate. When a loan is set up, the number of payments and the repayment amounts are established. Since the loan acquires interest throughout the transaction, this means future payments must pay back both principal and interest. Ultimately, all loan payments together need to fully reimburse the lender for the full amount of the principal.
Present Value Principle for Loans
The present value principle for loans states that the present value of all payments on a loan is equal to the principal that was borrowed. As illustrated in the timeline, taking all future payments and removing the interest, the payments must total to the original principal amount on the initial date of the loan. The interest rate used in this calculation is the interest rate for the loan itself.
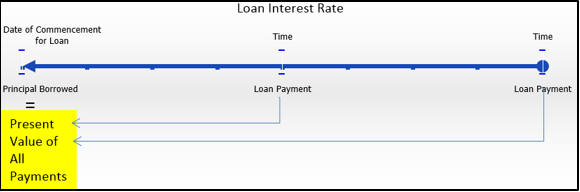
This relationship can be expressed as follows:
\[\text{Principal Borrowed }=\text{ Present Value of All Payments}\nonumber \]
How It Works
When you work with loans, the most common unknown variables are either the principal borrowed or the amount(s) of any unknown payment(s). You follow the same steps as for equivalent payments, discussed earlier in this section.
For example, assume a loan requires two equal payments of $1,000 semi-annually and you want to know the original principal of the loan. The loan’s interest rate is 7.1% compounded semi-annually.
Step 1:The timeline is illustrated here.
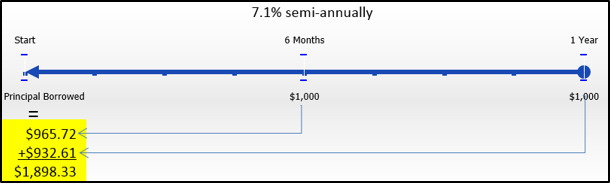
Step 2: According to the present value principle for loans, when you bring the two payments back to the starting date of the loan (the focal date), then the sum of the present values equals the initial amount borrowed.
Step 3: The \(IY\) = 7.1% and \(CY\) = 2, therefore \(i=7.1 \% / 2=3.55 \%\).
Step 4: The first payment needs to come back a \(\dfrac{1}{2}\) year, or \(N=2 \times \dfrac{1}{2}=1\). The second payment needs to come back 1 year, or \(N=2 \times 1=2\).
Step 5: Applying Formula 9.3, for the first payment \(\$ 1,000=PV(1+0.0355)^{1}\) or \(PV=\$ 965.717044\). For the second payment, \(\$ 1,000=P V(1+0.0355)^{2}\) or \(PV=\$ 932.609410\).
Step 6: The amount borrowed is the sum of the two present values, or \(\$ 965.717044+\$ 932.609410=\$ 1,898.33\). At 7.1% semi-annually, two payments of $1,000 semi-annually pay off a loan of $1,898.33.
Paths To Success
You can still use the time value of money buttons on your calculator to perform calculations involving unknown variables. Recall from the algebra discussion in Section 2.4 that any algebraic term consists of both a numerical and a literal coefficient. To move an unknown variable through time, enter the numerical coefficient of the variable into the calculator and compute its new value at the focal date. This new value on its focal date must then have the literal coefficient written after it before you proceed with further operations.
For example, if you want to perform a present value calculation on a future value of \(2y\), enter the numerical coefficient “2” as your \(FV\) and compute the \(PV\). Suppose the \(PV\) is 1.634. The literal coefficient has not disappeared. You just could not enter the letter on the calculator. Therefore, copying the literal coefficient to the present value yourself, you see that \(PV = 1.634y\). Example \(\PageIndex{3}\) applies this concept.
- The principal on a loan is $10,000 and two payments are required. If the first payment is $5,000, what statement could you make about the second payment?
- Consider two loans. The first requires four $2,500 quarterly payments. The second loan requires four $2,500 monthly payments. Assuming equal interest rates, what statement could you make about the principals of these two loans?
- Answer
-
- The principal is less than $8,000 since all four payments must have the interest removed.
- The second payment is more than $5,000 since it must pay back the interest as well as the remaining principal.
- The principal on the second loan is larger since the payments are made for only four months afterwards, so they involve relatively little interest. The first loan’s payments extend for one year, so it requires the removal of larger sums of interest to arrive at the principal
A $24,000 loan at 7% compounded semi-annually requires three payments at 1½ years, 3 years, and 4 years. The first payment is $3,000 and the second payment is three times as large as the final payment. Calculate the values of the second and third payments on the loan.
Solution
Find the amount of the second and third payments. Since the second payment is three times the size of the third payment, solve for the third payment, or \(x\), and then calculate the second payment afterwards.
What You Already Know
Step 1:
The principal, payment amounts, interest rate, and dates are known, as indicated on the timeline.
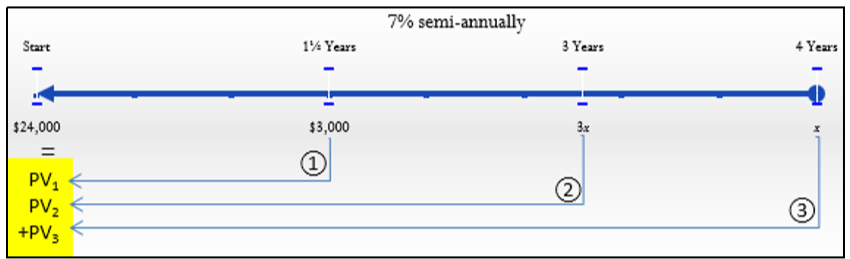
\(IY\) = 7%; \(CY\) = 2 Note: If the final payment is x and the second payment is three times as large, then it equals \(3x\).
How You Will Get There
Step 2:
The focal date is the start of the loan.
Step 3:
Calculate the periodic interest rate by applying Formula 9.1.
Step 4:
For each payment, calculate the number of compound periods by applying Formula 9.2.
Step 5:
For each payment apply Formula 9.3.
Step 6:
Using the present value principle for loans, equate the payments and the principal, then solve for the unknown variable \(x\).
\(\text { Principal }=PV_{1}+PV_{2}+PV_{3}\)
Once you know \(x\), calculate the size of the second payment = \(3x\).
Perform
Step 3:
\[i=\dfrac{7 \%}{2}=3.5 \%=0.035 \nonumber \]
Steps 4 and 5:
Using the circled number references in the timeline:
① \(N=2 \times 11 / 2=3 ; \$ 3,000=PV_{1}(1+0.035)^{3} ; PV_{1}=\dfrac{\$ 3,000}{1.035^{3}}=\$ 2,705.828117\)
② \(N=2 \times 3=6 ; 3 x=PV_{2}(1+0.035)^{6} ; PV_{2}=\dfrac{3 x}{1.035^{6}}=2.440501 x\)
③ \(N=2 \times 4=8 ; x=PV_{3}(1+0.035)^{8} ; PV_{3}=\dfrac{x}{1.035^{8}}=0.759411 x\)
Step 6:
\[\begin{aligned}
\$ 24,000 &=\$ 2,705.828117+2.440501 x+0.759411 x \\
\$ 24,000 &=\$ 2,705.828117+3.199913 x \\
\$ 21,294.17188 &=3.199913 x \\
\$ 6,654.61 &=x
\end{aligned} \nonumber \]
Solving for the \(3x\) payment: \(3($6,654.61) = \$19,963.83\)
Calculator Instructions
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| ① | 3 | 7 | Answer: $ 2,705.828117 | 0 | -3000 | 2 | 2 |
| ② | 6 | \(\surd\) | Answer: 2.440501 | \(\surd\) | 2500 | \(\surd\) | \(\surd\) |
| ③ | 8 | \(\surd\) | Answer: 0.759411 | \(\surd\) | -1 | \(\surd\) | \(\surd\) |
The second payment, located three years from the start of the loan, is $19,963.83, which is three times the size of the final payment of $6,654.61 one year later.


