9.6: Equivalent and Effective Interest Rates
- Page ID
- 22122
How can you compare interest rates posted with different compounding? For example, let’s say you are considering the purchase of a new home, so for the past few weeks you have been shopping around for financing. You have spoken with many banks as well as onsite mortgage brokers in the show homes. With semi-annual compounding, the lowest rate you have come across is 6.6%. In visiting another show home, you encounter a mortgage broker offering a mortgage for 6.57%. In the fine print, it indicates the rate is compounded quarterly. You remember from your business math class that the compounding is an important component of an interest rate and wonder which one you should choose—6.6% compounded semi-annually or 6.57% compounded quarterly.
When considering interest rates on loans, you clearly want the best rate. If all of your possible loans are compounded in the same manner, selecting the best interest rate is a matter of picking the lowest number. However, when interest rates are compounded differently the lowest number may in fact not be your best choice. For investments, on the other hand, you want to earn the most interest. However, the highest nominal rate may not be as good as it appears depending on the compounding.
To compare interest rates fairly and select the best, they all have to be expressed with equal compounding. This section explains the concept of an effective interest rate, and you will learn to convert interest rates from one compounding frequency to a different frequency.
Effective Interest Rates
If you place $1,000 into an investment earning 10% compounded semi-annually, how much will you have in your account after one year? Less than $1,100, exactly $1,100, or more than $1,100? If you say more than $1,100, you are absolutely correct. In other words, the 10% nominal rate does not fully reflect the true amount of interest that the investment earns annually, which depends on how often the principal increases. This raises two questions:
- What exact amount of interest is earned annually?
- What annual interest rate is truly being earned?
The effective interest rate is the true annually compounded interest rate that is equivalent to an interest rate compounded at some other (non-annual) frequency. In other words, the amount of interest accrued at the effective interest rate once in an entire year exactly equals the amount of interest accrued at the periodic interest rate successively compounded the stated number of times in a year. To calculate the effective interest rate, you must convert the compounding on the nominal interest rate into an annual compound.
The Formula
To see how the formula develops, take a $1,000 investment at 10% compounded semi-annually through a full year.
Start with \(PV=\$ 1,000, IY=10 \%\), and \(CY=2\) (semi-annually). Therefore, \(i=10 \% / 2=5 \%\). Using Formula 9.3, after the first six-month compounding period (\(N = 1\)) the investment is worth
\[FV=\$ 1,000(1+0.05)^{1}=\$ 1,050\nonumber \]
With this new principal of \(PV = \$1,050\), after the next six-month compounding period the investment becomes
\[FV=\$ 1,050(1+0.05)^{1}=\$ 1,102.50\nonumber \]
Therefore, after one year the investment has earned $102.50 of interest. Notice that this answer involves compounding the periodic interest twice, according to the compounding frequency of the interest rate. What annually compounded interest rate would produce the same result? Try 10.25% compounded annually. With \(PV=\$ 1,000, IY=10.25 \%\), and \(CY=1\), then \(i=10.25 \% / 1=10.25 \%\). Thus, after a year
\[FV=\$ 1,000(1+0.1025)^{1}=\$ 1,102.50\nonumber \]
This alternative yields the same amount of interest, $102.50. In other words, 10.25% compounded annually produces the same result as 10% compounded semi-annually. Hence, the effective interest rate on the investment is 10.25%, and this is what the investment truly earns annually.
Generalizing from the example, you calculate the future value and interest amount for the rate of 10% compounded semi-annually using the formulas
\[FV=PV(1+i)(1+i) \quad \text { and } \quad I=FV-PV\nonumber \]
Notice that the periodic interest is compounded by a factor of \((1+i)\) a number of times equaling the compounding frequency (\(CY=2\)). You then rewrite the future value formula:
\[FV=PV(1+i)^{CY}\nonumber \]
Substituting this into the interest amount formula, \(I=FV-PV\), results in
\[I=PV(1+i)^{CY}-PV\nonumber \]
Factor and rearrange this formula:
\[I=PV\left((1+i)^{CY}-1\right)\nonumber \]
\[\dfrac{I}{PV}=(1+i)^{CY}-1\nonumber \]
On the left-hand side, the interest amount divided by the present value results in the interest rate:
\[\text { rate }=(1+i)^{CY}-1\nonumber \]
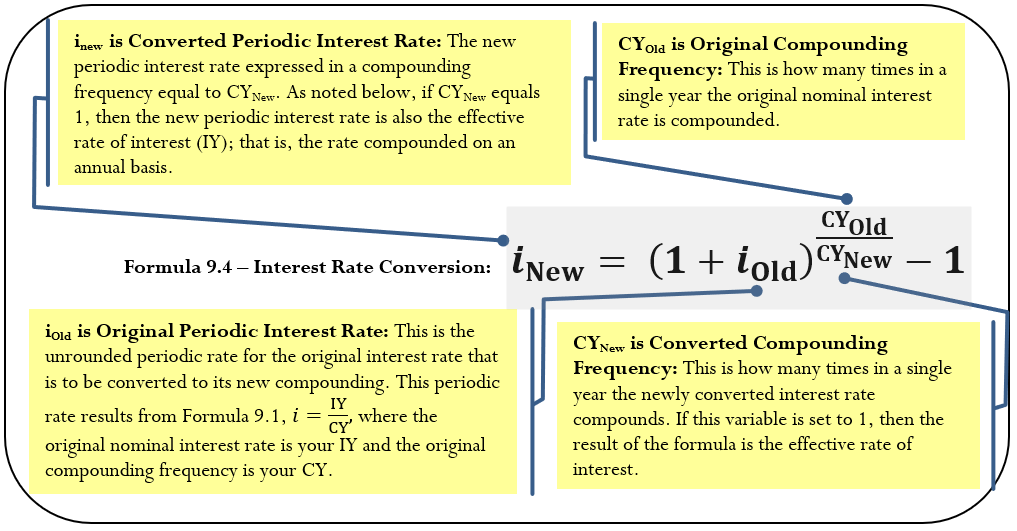
Formula 9.4 expresses this equation in terms of the variables for time value of money. It further adapts to any conversion between different compounding frequencies.
How It Works
Follow these steps to calculate effective interest rates:
Step 1: Identify the known variables including the original nominal interest rate (\(IY\)) and original compounding frequency (\(CY_{Old}=1\)). Set the \(CY_{New}=1\).
Step 2: Apply Formula 9.1 to calculate the periodic interest rate (\(i_{Old}\)) for the original interest rate.
Step 3: Apply Formula 9.4 to convert to the effective interest rate. With a compounding frequency of 1, this makes \(i_{New}=IY\) compounded annually.
Revisiting the opening scenario, comparing the interest rates of 6.6% compounded semi-annually and 6.57% compounded quarterly requires you to express both rates in the same units. Therefore, you could convert both nominal interest rates to effective rates.
| 6.6% compounded semi-annually | 6.57% compounded quarterly | |
|---|---|---|
| Step 1 | \(IY = 6.6%; CY_{Old} = 2; CY_{New} = 1\) | \(IY = 6.57%; CY_{Old} = 4; CY_{New} = 1\) |
| Step 2 | \(i_{Old} = 6.6%/2 = 3.3%\) | \(i_{Old} =6.57%/4 = 1.6425%\) |
| Step 3 | \(i_{New} = (1 + 0.033)^{2/1} − 1 = 6.7089%\) | \(i_{New} = (1 + 0.016425)^{4/1} − 1 = 6.7336%\) |
The rate of 6.6% compounded semi-annually is effectively charging 6.7089%, while the rate of 6.57% compounded quarterly is effectively charging 6.7336%. The better mortgage rate is 6.6% compounded semi-annually, as it results in annually lower interest charges.
Important Notes
The Texas Instruments BAII Plus calculator has a built-in effective interest rate converter called ICONV located on the second shelf above the number 2 key. To access it, press 2nd ICONV. You access three input variables using your ↑ or ↓scroll buttons. Use this function to solve for any of the three variables, not just the effective rate.
| Variable | Description | Algebraic Symbol |
|---|---|---|
| NOM | Nominal Interest Rate | \(IY\) |
| EFF | Effective Interest Rate | \(i_{New}\) (annually compounded) |
| C/Y | Compound Frequency | \(CY\) |
To use this function, enter two of the three variables by keying in each piece of data and pressing ENTER to store it. When you are ready to solve for the unknown variable, scroll to bring it up on your display and press CPT. For example, use this sequence to find the effective rate equivalent to the nominal rate of 6.6% compounded semi-annually:
\[2 \mathrm{nd} \text{ } \mathrm{ICONV}, 6.6 \text { Enter } \uparrow, 2 \text { Enter } \uparrow, \mathrm{CPT}\nonumber \]
\[\text{Answer: }6.7089\nonumber \]
Paths To Success
Annually compounded interest rates can be used to quickly answer a common question: "How long does it take for my money to double?" The Rule of 72 is a rule of thumb stating that 72% divided by the annually compounded rate of return closely approximates the number of years required for money to double. Written algebraically this is
\[\text{Approximate Years } =\dfrac{72 \%}{IY\text { annually }}\nonumber \]
For example, money invested at 9% compounded annually takes approximately \(72 \div 9 \%=8\) years to double (the actual time is 8 years and 15 days). Alternatively, money invested at 3% compounded annually takes approximately \(72 \div 3 \%=24\) years to double (the actual time is 23 years and 164 days). Note how close the approximations are to the actual times.
- borrowing?
- Answer
-
- The effective rate is equal to or higher than the nominal rate.
-
- 9%. since more interest is earned
- 8%, since less interest is paid
- Eighteen years, since a higher rate takes less time to double
If your investment earns 5.5% compounded monthly, what is the effective rate of interest? According to the Rule of 72, approximately how long will it take your investment to double at this effective rate?
Solution
Calculate the effective rate of interest (\(i_{New}\)). Once known, apply the Rule of 72 to approximate the doubling time.
What You Already Know
Step 1:
The original nominal interest rate and compounding along with the new compounding are known: \(IY = 5.5%; CY_{Old}\) = monthly = 12; \(CY_{New}\) = 1
How You Will Get There
Step 2:
Apply Formula 9.1 to the original interest rate.
Step 3:
Apply Formula 9.4, where \(i_{New} = IY\) annually.
Step 4:
To answer approximately how long it will take for the money to double, apply the Rule of 72.
Perform
Step 2:
\[i_{Old}=\dfrac{5.5 \%}{12}=0.458 \overline{3} \% \nonumber \]
Step 3:
\[i_{New}=(1+0.00458 \overline{3})^{\frac{12}{1}}-1=0.056408=5.6408 \% \nonumber \]
Step 4:
\[\text { Approximate Years }=\dfrac{72 \%}{5.6408 \%}=12.76 \nonumber \]
Calculator Instructions
2nd ICONV
| NOM | C/Y | EFF |
|---|---|---|
| 5.5 | 12 | Answer: 5.640786 |
You are effectively earning 5.6408% interest per year. At this rate of interest, it takes approximately 12¾ years, or 12 years and 9 months, for the principal to double.
As you search for a car loan, all banks have quoted you monthly compounded rates (which are typical for car loans), with the lowest being 8.4%. At your last stop, the credit union agent says that by taking out a car loan with them, you would effectively be charged 8.65%. Should you go with the bank loan or the credit union loan?
Solution
Since it is normal for a car loan to be compounded monthly, convert the effective rate to a monthly rate (\(IY\)) so that it matches all the other quotes.
What You Already Know
Step 1:
The effective rate and the compounding are as follows: \(i_{New} = 8.65%; CY_{Old}\) = monthly = 12; \(CY_{New}\) = 1
How You Will Get There
(Note: In this case, the \(i_{New}\) is known, so the process is reversed to arrive at the \(IY\). Thus, steps 2 and 3 are performed in the opposite order.)
Step 2:
Substitute into Formula 9.4, rearrange, and solve for \(i_{Old}\).
Step 3:
Substitute into Formula 9.1, rearrange, and solve for \(IY\).
Perform
Step 2:
\[\begin{aligned} &0.0865=\left(1+i_{Old}\right)^{12 \div 1}-1\\ &1.0865=\left(1+i_{Old}\right)^{12}\\ &1.0865^{1 / 12}=1+i_{Old}\\ &1.006937=1+i_{\text {Old }} \\ &0.006937=i_{\text {Old }} \end{aligned} \nonumber \]
Step 3:
\[\begin{aligned} 0.006937 &=\dfrac{IY}{12} \\ IY &=0.083249 \text { or } 8.3249 \% \end{aligned} \nonumber \]
Calculator Instructions
2nd ICONV
| NOM | C/Y | EFF |
|---|---|---|
| Answer: 8.324896 | 12 | 8.65 |
The offer of 8.65% effectively from the credit union is equivalent to 8.3249% compounded monthly. If the lowest rate from the banks is 8.4% compounded monthly, the credit union offer is the better choice.
Equivalent Interest Rates
At times you must convert a nominal interest rate to another nominal interest rate that is not an effective rate. For example, in the opening scenario of this section your mortgage rates were all quoted semi-annually except for one monthly rate. One way to compare these rates was to make them all effective rates. An alternative is to take the "oddball" rate and convert it to match the compounding of all the other rates. This brings up the concept of equivalent interest rates, which are interest rates with different compounding that produce the same effective rate and therefore are equal to each other. After one year, two equivalent rates have the same future value.
How It Works
To convert nominal interest rates you need no new formula. Instead, you make minor changes to the effective interest rate procedure and add an extra step. Follow these steps to calculate any equivalent interest rate:
Step 1: For the nominal interest rate that you are converting, identify the nominal interest rate (IY) and compounding frequency (\(CY_{Old}\)). Also identify the new compounding frequency (\(CY_{Old}=1\)).
Step 2: Apply Formula 9.1 to calculate the original periodic interest rate (\(i_{Old}=1\)).
Step 3: Apply Formula 9.4 to calculate the new periodic interest rate (\(i_{New}\)).
Step 4: Apply Formula 9.1 using \(i_{New}\) and \(CY_{New}\),rearrange, and solve for the new converted nominal interest rate (\(IY\)).
Once again revisiting the mortgage rates from the section opener, compare the 6.6% compounded semi-annually rate to the 6.57% compounded quarterly rate by converting one compounding to another. It is arbitrary which interest rate you convert. In this case, choose to convert the 6.57% compounded quarterly rate to the equivalent nominal rate compounded semi-annually.
Step 1: The original nominal interest rate \(IY=6.57 \%\) and the \(CY_{Old}=\text { quarterly }=4 . \text { Convert to } CY_{New}=\text { semi-annually }=2\).
Step 2: Applying Formula 9.1, \(i_{\text{old}}=6.57 \% / 4=1.6425 \%\).
Step 3: Applying Formula 9.4, \(i_{\text {New }}=(1+0.016425)^{4\div 2}-1=0.033119\)
Step 6: Applying Formula 9.1, \(0.033119=\dfrac{I Y}{2}\) or \(IY=0.06624\).
Thus, 6.57% compounded quarterly is equivalent to 6.624% compounded semi-annually. Pick the mortgage rate of 6.6% compounded semi-annually since it is the lowest rate available. Of course, this is the same decision you reached earlier.
Important Notes
Converting nominal rates on the BAII Plus calculator takes two steps:
Step 1: Convert the original nominal rate and compounding to an effective rate. Input NOM and C/Y, then compute the EFF.
Step 2: Input the new C/Y and compute the NOM.
For the mortgage rate example above, use this sequence:
\[2\text{nd ICONV} , 6.57 \text { Enter } \uparrow, 4 \text { Enter } \uparrow, \text {CPT} \downarrow, 2 \text { Enter } \downarrow, \text {CPT}\nonumber \]
\[\text{Answer: }6.623956\nonumber \]
A good way to memorize this technique is to remember to "go up then down the ladder." To convert a nominal rate to an effective rate, you press "\(\uparrow\)" twice. To convert an effective rate back to a nominal rate, you press "\(\downarrow\)" twice. Hence, you go up and down the ladder!
Things To Watch Out For
When converting interest rates, the most common source of error lies in confusing the two values of the compounding frequency, or \(CY\). When working through the steps, clearly distinguish between the old compounding (\(CY_{Old}\)) that you want to convert from and the new compounding (\(CY_{New}\)) that you want to convert to. A little extra time spent on double-checking these values helps avoid mistakes.
- If you convert a quarterly rate into a monthly rate, is the converted nominal rate higher or lower?
- Answer
-
- Higher. The interest is placed into the account less frequently, so more interest needs to go in each time.
- Lower. The interest is placed into the account more frequently, so less interest is needed each time.
You are looking at three different investments bearing interest rates of 7.75% compounded semi-annually, 7.7% compounded quarterly, and 7.76% compounded semi-annually. Which investment offers the highest interest rate?
Solution
Notice that two of the three interest rates are compounded semi-annually while only one is compounded quarterly. Although you could convert all three to effective rates (requiring three calculations), it is easier to convert the quarterly compounded rate to a semi-annually compounded rate. Then all rates are compounded semi-annually and are therefore comparable.
What You Already Know
Step 1:
The original interest rate and compounding are known: \(IY\) = 7.7%; \(CY_{Old}\) = quarterly = 4; \(CY_{New}\) = semi-annually = 2
How You Will Get There
Step 2:
Apply Formula 9.1 to the original interest rate.
Step 3:
Convert the original interest rate to its new periodic rate using Formula 9.4.
Step 4:
Substitute into Formula 9.1 and rearrange for \(IY\).
Perform
Step 2:
\[i_{Old}=\dfrac{7.7 \%}{4}=1.925 \% \nonumber \]
Step 3:
\[i_{New}=(1+0.01925)^{4\div2}-1=0.038870 \nonumber \]
Step 4:
\[\begin{aligned} 0.038870 &=\dfrac{IY}{2} \\ IY &=0.077741 \text { or } 7.7741 \%\end{aligned} \nonumber \]
Calculator Instructions
2nd ICONV
| Steps | NOM | C/Y | EFF |
|---|---|---|---|
| 1-3 | 7.7 | 4 | Answer: 7.925204 |
| 4-6 | Answer: 7.774112 | 2 | \(\surd\) |
The quarterly compounded rate of 7.7% is equivalent to 7.7741% compounded semi-annually. In comparison to the semi-annually compounded rates of 7.75% and 7.76%, the 7.7% quarterly rate is the highest interest rate for the investment.


