12.3: Perpetuities
- Page ID
- 22140
Some of the scholarships offered to students at your college were created decades ago, yet these scholarships continue to pay out money to students each and every year. Where does all of the money come from? Did somebody bestow a tremendously large endowment fund all those many years ago to sustain the scholarship over decades? Or does an individual or supporting organization simply pay it out of pocket each year? How is it possible for these scholarships to pay out through all the past years and all of the foreseeable years?
What would you do if you win a large lottery prize such as Lotto 6/49 or Lotto Max? Today’s headlines continually showcase lottery winners who win "the big one," becoming overnight millionaires. With their new-found earnings, they rush out to buy million dollar homes and luxury vehicles and indulge in the pleasures of life. Sometime shortly thereafter, stories are told about how these millionaires file for bankruptcy. What if someone had told these people that instead of spending the money all at once, they could invest it and use the interest to live on forever; whole generations of their family could benefit from the winnings. Just imagine: if you invest $5 million at 5% interest, you would earn $250,000 of interest each and every year that you could withdraw endlessly.
These scenarios highlight the importance of perpetuities, which are annuities that have an infinite term. At your individual level, any sum of money you invest as a perpetuity can be used to generate income forever. At the professional level, many companies and not-for-profit organizations such as sports clubs establish scholarship programs and bursaries for their employees, members, or clients. In some contracts, payments such as royalties continue forever. Some divided stocks have their price determined by indefinite future dividend amounts.
This section explores the concept of perpetuities. You will calculate the investment required to sustain a perpetuity along with the payment amount.
What Are Perpetuities?
A perpetuity is a special type of annuity that has fixed, regular payments continuing indefinitely. If the principal of the investment is never withdrawn, then the interest earned each period can be withdrawn without affecting the future interest earnings of the investment. Therefore, the annuity continues to earn the same amount of interest each and every future interval and can pay out interest forever. How can a single deposit of principal sustain an infinite amount of payments? Mathematically, money that occurs in a far distant future becomes worthless when it is brought back to today, where it has no value.
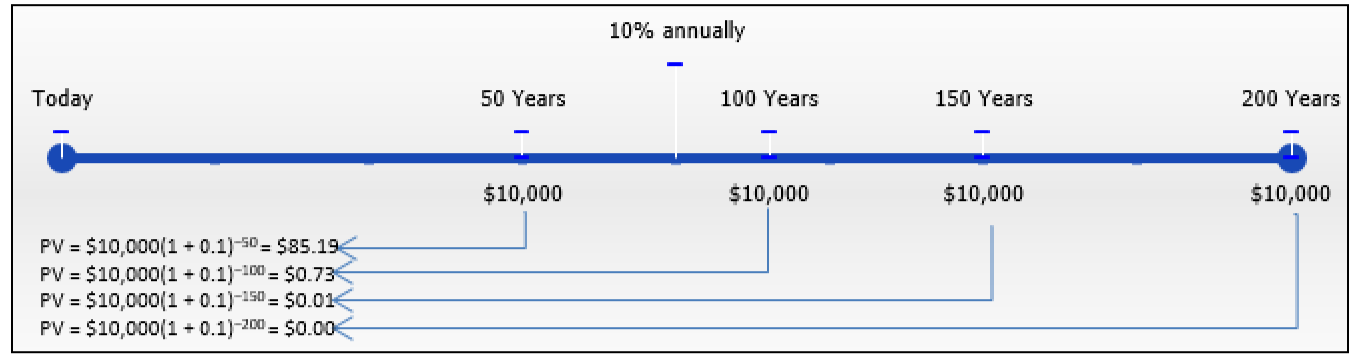
To illustrate the point of money being worthless today, the figure here calculates some present values of $10,000 payments that occur far into the future. Through the various calculations, notice that when the payments occur farther into the future the present value diminishes to practically nothing. In fact, after about 160 years the $10,000 becomes worth almost $0 today. Any payments made after this point in time result in such minuscule additions to the present value that in essence they really have no further impact. Under this premise, it is then possible to determine a value today that is equivalent to the infinite future annuity payment stream.
Ordinary Perpetuities and Perpetuities Due
A perpetuity is a special type of annuity. It comes in both ordinary and annuity due types. As well, the payment frequency and compounding frequency create either a simple or general annuity structure. Perpetuities can even occur after a deferral period, and hence deferred perpetuities are possible.
A typical timeline for a perpetuity appears here. It is identical to any other annuity timeline except for two distinguishing characteristics:

- Future Time Period. Instead of a specific time period being indicated on the right-hand side of the timelines, the word “Forever” appears, to represent the infinite nature of the perpetuity.
- Equivalency of \(FV\) and \(PV\). The future value of the perpetuity is the same as the present value since only the interest is ever paid out and the principal is never touched.
The Formula
Like the annuity formulas, the perpetuity formulas are designed to accommodate both simple and general annuities through the \(\dfrac{CY}{PY}\) exponent, which ensures that the compounding interval matches the payment interval. These new formulas represent simplified versions of Formulas 11.4 and 11.5. To illustrate, recall Formula 11.4:
\[PV_{ORD}=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}}{(1+i)^{\frac{CY}{PY}-1}}\right] \nonumber \]
Looking at the numerator, as \(N\) becomes increasingly larger the \(\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}\) approaches a value of zero, which effectively removes it from the equation. This leaves a numerator of 1 over the denominator.

How It Works
The steps required to solve for the present value of a perpetuity remain essentially unchanged from solving for the present value of any annuity. These steps, introduced in Section 11.3, are reviewed for the case of perpetuities:
Step 1: Identify the perpetuity type. Draw a timeline to visualize the question.
Step 2: Identify the variables that may be known, including \(IY, CY, PMT, PY\), and either \(PV_{ORD}\) or \(PV_{DUE}\). If a \(PV_{ORD}\) or \(PV_{DUE}\) is known, then set the \(FV\) to the same amount. If no present value is known, then set \(FV\) to $0, since money in the distant future is worthless. Unlike in regular annuities, you do not need to identify Years because of the absence of N from all perpetuity calculations.
Step 3: Use Formula 9.1 to calculate \(i\).
Step 4: You never require this step since the \(FV\) is located so far into the future that you can automatically ascertain that its present value is equal to zero.
Step 5: To calculate the present value, apply either Formula 12.5 or Formula 12.6, depending on the type of perpetuity.
As with regular annuities, if you are dealing with a deferred perpetuity then you must modify these procedures as you would to calculate deferred annuities (refer to Section 12.1). Most perpetuity applications require you to calculate either the investment needed (\(PV_{ORD}\) or \(PV_{DUE}\)) or the payment (\(PMT\)). Use algebraic substitution and rearrangement when other variables are required.
Important Notes
The BAII Plus calculator is set up for fixed term annuities only. Therefore, it has no specific built-in function or manner in which to enter a perpetuity. However, since a perpetuity is a specialized version of a regular annuity, a few minor adaptations to the annuity inputs allow you to calculate perpetuities. Input all variables as usual except for the changes shown in the table below.
| Variable | Solving for \(PV_{ORD}\) or \(PV_{DUE}\) | Solving for PMT |
|---|---|---|
| FV | Assign FV = 0 since money in the distant future is worthless today. | Assign FV equal to either PVORD or PVDUE, whichever is known. Recall that the principal is never touched. |
| N | Use a large value such as 10,000.* | Use a large value such as 2,500.* |
* This will place the FV far into the distant future. A larger value could be used, but this must be done with caution. Depending on the quantities appearing in the perpetuity calculation, the power resulting from the exponent of a very large N may exceed the computational abilities of the technology and produce an error. If you experience an error, try lowering the value of \(N\) by a little bit.
Paths To Success
Formulas 12.5 and 12.6 represent simplified versions of Formulas 11.4 and 11.5. If you find these new formulas confusing, or if you just want to remember a single formula for present values, you can solve any perpetuity question with the Chapter 11 formulas. If you use these formulas, you must substitute an extremely large value of N into the formula using the technology substitutions discussed in the table above.
- If a single payment is placed today into an ordinary perpetuity, will its future value be higher, lower, or the same?
- If a lump sum is placed today into a perpetuity due, will its future value be higher, lower, or the same?
- Answer
-
- It is the same after every withdrawal of interest and higher between withdrawals.
- It is the same immediately before any withdrawal of interest and always lower between withdrawals. Recall that the first payment is withdrawn immediately, resulting in a principal that remains smaller than the original amount
Kendra is the human resources director and wants to offer a new employee perk through a corporate scholarship program. Each year, 10 $1,000 scholarships are to be made available to the children of the company's employees. If the first scholarships are to be offered annually starting one year from now, what amount must be invested today at 7.5% compounded annually to fund the scholarship program in perpetuity?
Solution
Step 1:
Calculate an amount today that must be invested such that it can pay out the needed funds at the end of every year in perpetuity. Payment and compounding intervals are the same, therefore this is an ordinary simple perpetuity. Determine the present value (\(PV_{ORD}\)).
What You Already Know
Step 1 (continued):
The timeline for the perpetuity appears below.

Step 2:
\(IY\) = 7.5%, \(CY\) = 1, \(PMT\) = 10 × $1,000 = $10,000, \(PY\) = 1
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Not needed for perpetuities.
Step 5:
Apply Formula 12.5.
Perform
Step 3:
\(i=7.5 \% / 1=7.5 \%\)
\[PV_{ORD}=\dfrac{\$ 10,000}{(1+0.075)^{\frac{1}{1}}-1}=\$ 133,333.33 \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| END | 10000 | 7.5 | Answer: -133,333.3333 | 10000 | 0 | 1 | 1 |
If Kendra has her company place $133,333.33 into the perpetuity account, it will earn $10,000 interest at 7.5% compounded annually each year, which will fund the scholarship program in perpetuity.
In memory of his late father, who was a highly successful marketing manager, Brian would like to set up a marketing scholarship program with his university's school of business. He is able to donate $100,000 from his father's estate to set up the fund. If the perpetuity fund can earn 6.3% compounded semi-annually and the first scholarship is to be provided immediately, what annual scholarship amount can the fund offer?
Solution
Step 1:
Calculate the amount of the perpetuity payment that the contribution can sustain. Payments and compounding intervals are different, while payments start immediately. Therefore, this is a general perpetuity due. Determine the perpetuity payment amount (PMT).
What You Already Know
Step 1 (continued):
The timeline for the scholarship appears below.

Step 2:
\(IY\) = 6.3%, \(CY\) = 2, \(PV_{DUE}\) = $100,000, \(PY\) = 1
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Not needed in perpetuities.
Step 5:
Substitute into Formula 12.6, rearranging for \(PMT\).
Perform
Step 3:
\(i=6.3 \% / 2=3.15 \% \)
Step 5:
\[\$ 100,000=PMT\left(\dfrac{1}{(1+0.0315)^{\frac{2}{1}}-1}+1\right) \nonumber \]
\[\$ 100,000=PMT(16.626892) \nonumber \]
\[\$ 6,014.35=PMT \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 2500 | 6.3 | -100000 | Answer: 6,014.353018 | 100000 | 1 | 2 |
Brian's donation will allow an immediate scholarship amount of $6,014.35, which will leave $100,000 − $6,014.35 = $93,985.65 principal in the account. This principal amount will be able to earn $6,014.35 in perpetuity each year.
One of the methods for valuing common shares is to determine the present value of its future dividends. If IBM Corporation is forecast to have year-end dividends of $1.50 per share for the next three years followed by $1.80 per share in perpetuity, how much should an investor be willing to pay if he requires a 12% compounded quarterly rate of return?
Solution
Step 1:
There are different compounding and payments, and payments are made at the end of the interval. Therefore, this is a combination of an ordinary general annuity for the first three years followed by an ordinary general perpetuity. Calculate the present value of the common shares (\(PV_{ORD}\)).
What You Already Know
Step 1 (continued):
The timeline for the common shares appears below.
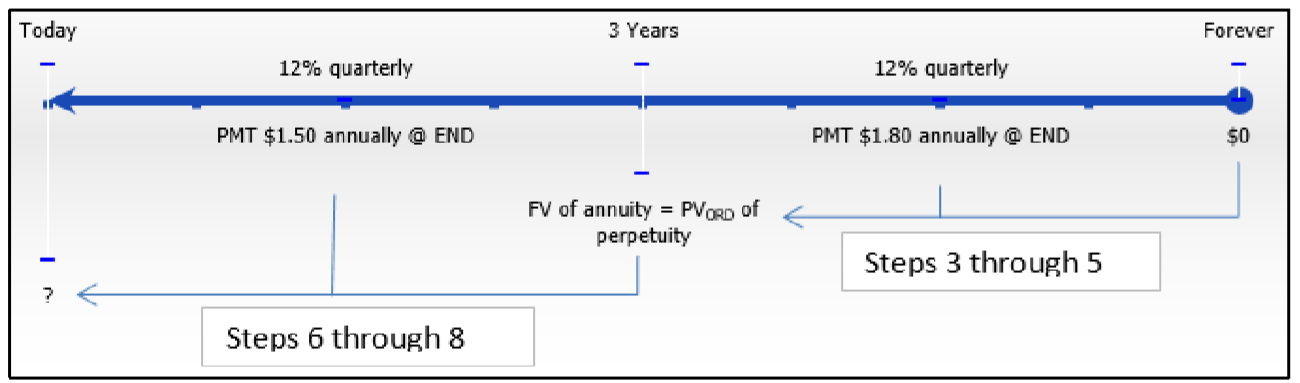
Step 2:
Ordinary General Perpetuity: \(IY\) = 12%, \(CY\) = 4, \(PMT\) = $1.80, \(PY\) = 1
How You Will Get There
Starting from the right side of the timeline, calculate the present value of the perpetuity first.
Step 3:
Apply Formula 9.1.
Step 4:
Not needed in perpetuities.
Step 5:
Apply Formula 12.5. Then calculate the present value of the three-year annuity.
Step 6:
Apply Formulas 9.2 and 9.5 (rearranging for \(PV\)) to find the future value single payment (which is the \(PV_{ORD}\) of the perpetuity).
Step 7:
Apply Formula 11.1 and Formula 11.4 to the annuity.
Step 8:
Add the results of step 6 and step 7 to get the share value today.
Perform
Step 3:
\(i=12 \% / 4=3 \%\)
Step 5:
\[PV_{ORD}=\dfrac{\$ 1.80}{(1+0.03)^{\frac{4}{1}}-1}=\$ 14.341622 \nonumber \]
Step 6:
\(N=4 \times 3=12 \text { compounds } \)
\[\$ 14.341622=PV(1+0.03)^{12} \nonumber \]
\[PV=\$ 14.341622 \div(1+0.03)^{12}=\$ 10.058925 \nonumber \]
Step 7:
\(N=1 \times 3=3 \text { payments }\)
\[PV_{ORD }=\$ 1.50\left[\dfrac{1-\left[\frac{1}{(1+0.03)^{\frac{4}{1}}}\right]^{3}}{(1+0.03)^{\frac{4}{1}}-1}\right]=\$ 3.568914 \nonumber \]
Step 8:
\[\$ 10.058925+\$ 3.568914=\$ 13.63 \nonumber \]
Calculator Instructions
| Steps | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 3 - 5 | END | 10000 | 12 | Answer: -14.341622 | 1.8 | 0 | 1 | 4 |
| 6 - 8 | \(\surd\) | 3 | \(\surd\) | Answer: -13.627839 | 1.5 | 14.341622 | \(\surd\) | \(\surd\) |
If an investor desires a 12% rate of return on his investment, he would be willing to pay $13.63 per share to receive the dividends in perpetuity.


