19.2.1: Degree and Radian Measure
- Page ID
- 70289
- Understand radian measure.
- Convert from degree to radian measure.
- Convert from radian to degree measure.
Introduction
You know that there can be different units of measurement to measure the same thing. For example, length can be measured in feet and meters and temperature can be measured in degrees Celsius and degrees Fahrenheit. We often use formulas to convert between different units of measurement.
There are also two ways to measure angles. You know how to measure them in degrees. Now you will learn how to measure them in radians and how to convert between these two measurements. While degree measure is used in everyday activities such as building construction and surveying land, radian measure is used for many calculations, such as the speed and distance traveled by satellites above the Earth’s surface, including the International Space Station! It is important to be able to measure angles in radians as well as in degrees and to be able to convert between the two systems.
Radian Measure
In order for us to be able to define radians, it is necessary to introduce the concept of a central angle. A central angle is an angle whose vertex is at the center of a circle. In the circle below, the center is point \(O\), the length of the radius is \(r\), and \(\angle AOB\) is a central angle.
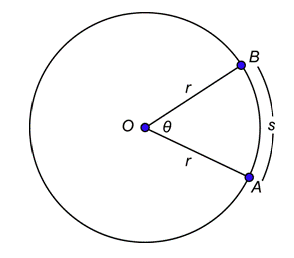
Notice that \(\angle AOB\) cuts off or determines an arc \(\stackrel{\large \frown}{AB}\) that has length \(s\). The radian measure of a central angle, often denoted by the Greek letter theta (\(\theta\)), is defined to be the ratio of the arc length to the length of the radius. So the radian measure of \(\angle AOB\) is given by:
\(\theta=\frac{\text { arc length }}{\text { radius length }}=\frac{s}{r}\)
Arc length, \(s\), and radius, \(r\), must be in the same units.
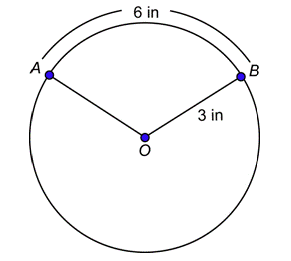
Problem: What is the radian measure of central angle \(AOB\)?
Answer
In this circle, \(r = 3\) inches. The arc determined by \(\angle AOB\) has length \(s = 6\) inches. Substitute these into the formula.
\(\theta=\frac{s}{r}=\frac{6 \text { inches }}{3 \text { inches }}=2\)
The measure of central angle \(AOB\) is 2 radians.
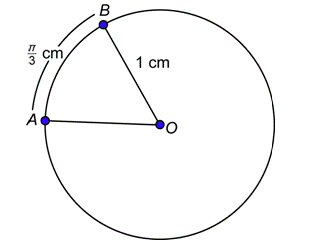
Problem: Find the measure of central angle \(AOB\) in radians.
Answer
In this circle, \(r = 1\) cm. The arc determined by \(\angle AOB\) has length \(s = \frac{\pi}{3}\) cm. Substitute these into the formula.
\(\theta=\frac{s}{r}=\frac{\frac{\pi}{3} \mathrm{~cm}}{1 \mathrm{~cm}}=\frac{\pi}{3}\)
The measure of central angle \(AOB\) is \(\frac{\pi}{3}\) radians.
What is the connection between degrees and radians? Let’s see what happens when the arc is the entire circle:
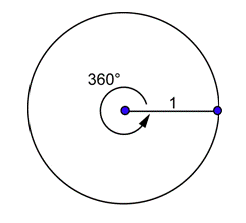
The circumference of this circle is given by \(C=2 \pi r=2 \pi \cdot 1=2 \pi\). This is the arc length of the entire circle, or the arc length corresponding to a central angle of \(360^{\circ}\). What is the radian measure of this angle?
\(\theta=\frac{\text { arc length }}{\text { radius length }}=\frac{2 \pi}{1}=2 \pi\)
A central angle of \(360^{\circ}\) has a radian measure of \(2\pi\). That is:
\(360^{\circ}=2 \pi \text { radians }\)
If you divide both sides by 2, you will obtain:
\(180^{\circ}=\pi \text { radians }\)
We’ll use this to convert from degrees to radians and vice versa.
While degrees are always written with a degree symbol (°), radians are usually written without any symbol or unit attached. So, for example, \(\tan 3^{\circ}\) means the tangent of an angle that measures \(3^{\circ}\), while \(\tan 3\) means the tangent of an angle that measures 3 radians.
Make sure that you use the same units of length for the length of the radius \(r\) and the arc length \(s\). In the first example, they were both in inches; in the second example, they were both in centimeters. When you divide, those units cancel, and you are left with a unitless number.
Problem: Find the measure of central angle \(AOB\) in radians.
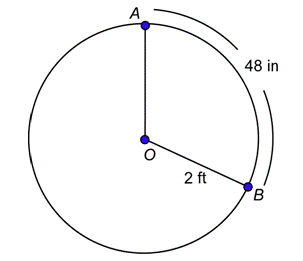
Answer
You want the arc length and the radius to have the same units, but they are given to you in inches and feet. You could convert either one. The arc determined by \(\angle AOB\) has length \(s = 48\) inches.
\(\begin{array}{l}
s =48 \text { inches } \\
\,\;\, =48 \text { inches } \cdot \frac{1 \text { foot }}{12 \text { inches }}\\
\,\\;\,=4 \text { feet }
\end{array}\)
In this circle, \(r = 2\) feet. Substitute this and the value above for \(s\) into the formula.
\(\theta=\frac{s}{t}=\frac{4 \text { feet }}{2 \text { feet }}=2\)
The measure of central angle \(AOB\) is 2 radians.
If you take the definition of radian measure, \(\theta = \frac{s}{r}\), and multiply both sides by r, you get the formula for arc length:
\(s=r \theta\)
Problem: The central angle shown has a measure of \(\frac{1}{2}\) radian. What is the length of \(\stackrel {\large \frown}{CD}\)?
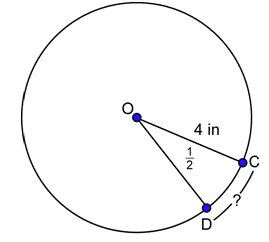
Answer
In this circle, \(r = 4\) inches. You know that \(\theta = \frac{1}{2}\). Substitute these numbers into the arc length formula.
\(s=r \theta=(4 \text { inches }) \cdot \frac{1}{2}=2 \text { inches }\)
The length of \(\stackrel {\large \frown}{CD}\) is 2 inches.
We have used \(\theta = \frac{s}{t}\) and \(s = r \theta\) to find the radian measure of the central angle as well as the arc length. But you can also use the arc length formula to find the length of the radius, as seen in the following example.
Problem: If the length of \(\stackrel {\large \frown}{EF}\) is 42 millimeters, and the measure of \(\angle EOF\) is 3 radians, what is the length of the radius of the circle?
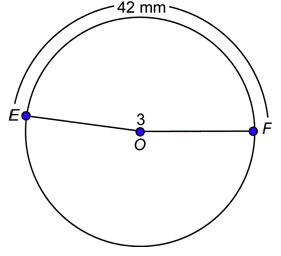
Answer
You are given that \(s = 42\) mm, and \(\theta = 3\). Substitute these values into the arc length formula.
\(\begin{array}{c}
s=r \theta \\
42 \mathrm{~mm}=r \cdot 3
\end{array}\)
Solve the equation for \(r\).
\(\frac{42 \mathrm{~mm}}{3}=r\)
Rewrite as a mixed number.
\(r=14 \mathrm{~mm}\)
The radius of the circle is 14 millimeters.
A circle has a radius of 8 inches and central angle \(AOB\) makes an arc \(AB\) of length 2 feet.
What is the radian measure of angle \(AOB\)?
- \(\frac{1}{4}\)
- \(\frac{1}{3}\)
- 3
- 4
- Answer
-
- \(\frac{1}{4}\). Incorrect. You probably divided 2 by 8. You need to convert the feet to inches so that you have the same units. The correct answer is 3.
- \(\frac{1}{3}\). Incorrect. You probably correctly converted both measurements to inches, but then divided the radius by the arc length. You need to divide the arc length by the radius. The correct answer is 3.
- 3. Correct. The arc length is 2 feet or 24 inches. Divide this by the radius, 8 inches, to get 3.
- 4. Incorrect. You probably divided 8 by 2. You need to convert the feet to inches so that you have the same units. You also need to divide the arc length by the radius. The correct answer is 3.
Converting from Degrees to Radians
Earlier we saw that \(180^{\circ}\) = \(\pi\) radians. Divide both sides of this equation by 180. You get:
\(1^{\circ}=\frac{\pi}{180} \text { radians }\)
You can use this to convert the measure of an angle from degrees to radians. For example, if you wanted to convert \(30^{\circ}\) to radians, you could multiply both sides by 30:
\(30^{\circ}=30 \cdot \frac{\pi}{180} \text { radians }=\frac{30 \pi}{180} \text { radians }=\frac{\pi}{6} \text { radians }\)
To say this another way, you multiply \(30^{\circ}\) by \(\frac{\pi}{180^{\circ}}\) to get \(\frac{\pi}{6}\) radians.
To convert \(60^{\circ}\) to radians, you multiply \(60^{\circ}\) by \(\frac{\pi}{180^{\circ}}\) to get \(\frac{\pi}{3}\) radians.
In a similar fashion, multiply any degree measure by \(\frac{\pi}{180^{\circ}}\) to convert it to radians.
Problem: Convert \(0^{\circ}\), \(45^{\circ}\), \(90^{\circ}\) to radians.
Answer
In each case, just multiply by \(\frac{\pi}{180^{\circ}}\) and simplify.
\(0^{\circ}=0^{\circ} \cdot \frac{\pi}{180^{\circ}} \text { radians }=0 \text { radians }\)
\(\begin{aligned}
45^{\circ} &=45^{\circ} \cdot \frac{\pi}{180^{\circ}} \text { radians } \\
&=\frac{45 \pi}{180} \text { radians } \\
&=\frac{\pi}{4} \text { radians }
\end{aligned}\)
\(\begin{aligned}
90^{\circ} &=90^{\circ} \cdot \frac{\pi}{180^{\circ}} \text { radians } \\
&=\frac{90 \pi}{180} \text { radians } \\
&=\frac{\pi}{2} \text { radians }
\end{aligned}\)
\(0^{\circ}=0 \text { radians, } 45^{\circ}=\frac{\pi}{4} \text { radians, } 90^{\circ}=\frac{\pi}{2} \text { radians }\)
Here is a chart with the angles that we have converted so far.
| Degree Measure | Radian Measure |
| \(0^{\circ}\) | 0 |
| \(30^{\circ}\) | \(\frac{\pi}{6}\) |
| \(45^{\circ}\) | \(\frac{\pi}{4}\) |
| \(60^{\circ}\) | \(\frac{\pi}{3}\) |
| \(90^{\circ}\) | \(\frac{\pi}{2}\) |
| \(180^{\circ}\) | \(\pi\) |
| \(360^{\circ}\) | \(2 \pi\) |
Here is the same information, with some additional angles, in a picture format:
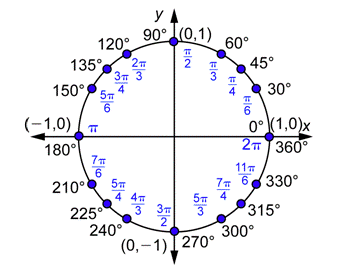
The same procedure works just as well for negative angles. Remember that a negative angle is just an angle that is oriented clockwise when drawn in standard position. A negative number of degrees becomes a negative number of radians.
How many radians are there in \(-120^{\circ}\)?
- \(\frac{\pi}{60}\)
- \(-\frac{2}{3}\)
- \(-\frac{3 \pi}{2}\)
- \(-\frac{2 \pi}{3}\)
- Answer
-
- \(\frac{\pi}{60}\). Incorrect. You may have correctly found \(-\frac{120 \pi}{180}\), but then reduced incorrectly. The correct answer is D.
- \(-\frac{2}{3}\). Incorrect. It looks like you divided by 180. You need to multiply by \(\frac{\pi}{180^{\circ}}\). The correct answer is D.
- \(-\frac{3 \pi}{2}\). Incorrect. You may have correctly found \(-\frac{120 \pi}{180}\), but made a mistake while reducing. The correct answer is D.
- \(-\frac{2 \pi}{3}\). Correct. Multiply by \(\frac{\pi}{180^{\circ}}\) to get \(-\frac{120 \pi}{180}=-\frac{2 \pi}{3}\).
Converting from Radians to Degrees
Suppose you had angles measured in radians and you wanted to know their degree measure. The procedure is similar to the one going from degrees to radians.
Again, you know that \(\pi\) radians \(= 180^{\circ}\). Divide both sides of this equation by \(\pi\). You get:
\(\text { radian }=\frac{180^{\circ}}{\pi}\)
If you wanted to convert \(\frac{\pi}{6}\) radians to degrees, you could multiply both sides of the above equation by \(\frac{\pi}{6}\):
\(\frac{\pi}{6} \cdot 1 \text { radian }=\frac{\pi}{6} \cdot \frac{180^{\circ}}{\pi}=\frac{180^{\circ}}{6}=30^{\circ}\)
To state this in another way, we multiplied \(\frac{\pi}{6}\) by \(\frac{180^{\circ}}{\pi}\) to get \(30^{\circ}\). In a similar fashion, multiply any radian measure by \(\frac{180^{\circ}}{\pi}\) to convert it to degrees.
Problem: Convert \(\frac{2 \pi}{3}\) and \(\frac{3 \pi}{4}\) to degrees.
Answer
In each case, just multiply by \(\frac{180^{\circ}}{\pi}\) and simplify.
\(\begin{aligned}
\frac{2 \pi}{3} &=\frac{2 \pi}{3} \cdot \frac{180^{\circ}}{\pi} \\
&=\frac{360^{\circ}}{3} \\
&=120^{\circ}
\end{aligned}\)
\(\begin{aligned}
\frac{3 \pi}{4} &=\frac{3 \pi}{4} \cdot \frac{180^{\circ}}{\pi} \\
&=\frac{540^{\circ}}{4} \\
&=135^{\circ}
\end{aligned}\)
\(\frac{2 \pi}{3}=120^{\circ}, \frac{3 \pi}{4}=135^{\circ}\)
Make sure that your answer has a degree symbol. An angle measure written without a degree symbol is always assumed to be in radians.
Here is a chart showing equivalent radian and degree measures for some common angles.
| Radian Measure | Degree Measure |
| 0 | \(0^{\circ}\) |
| \frac{\pi}{6} | \(30^{\circ}\) |
| \frac{\pi}{4} | \(45^{\circ}\) |
| \frac{\pi}{3} | \(60^{\circ}\) |
| \frac{\pi}{2} | \(90^{\circ}\) |
| \(\pi\) | \(180^{\circ}\) |
| \(2 \pi\) | \(360^{\circ}\) |
Problem: Convert 1 radian to degrees and give your answer to the nearest tenth of a degree.
Answer
Actually, you already know the value of 1 radian in degrees. However, you need to use a calculator to do the division and obtain a decimal.
\(\begin{aligned}
1 \text { radian } &=\frac{180^{\circ}}{\pi} \\
&=57.29577951^{\circ} \ldots \\
&=\approx 57.3^{\circ}
\end{aligned}\)
\(1 \text { radian } \approx 57.3^{\circ}\)
So 1 radian is a little less than \(60^{\circ}\), or a little less than one-sixth of a circle.
You can use the same procedure for negative angles.
What is the equivalent degree measure of \(-\frac{5 \pi}{6}\) radians written in simplest terms?
- \(150^{\circ}\)
- \(-150^{\circ}\)
- \(\frac{-900^{\circ}}{6}\)
- \(\frac{-\pi^{2}}{216}\)
- Answer
-
- \(150^{\circ}\). Incorrect. You probably correctly multiplied by \(\frac{180^{\circ}}{\pi}\), but you left out the negative sign. The correct answer is \(-150^{\circ}\).
- \(-150^{\circ}\). Correct. Multiply by \(\frac{180^{\circ}}{\pi}\) to get \(\frac{-900 \pi^{\circ}}{6 \pi}\), and then simplify the fraction.
- \(\frac{-900^{\circ}}{6}\). Incorrect. You probably correctly multiplied by \(\frac{180^{\circ}}{\pi}\), but you forgot to simplify. The correct answer is \(-150^{\circ}\).
- \(\frac{-\pi^{2}}{216}\). Incorrect. You multiplied by \(\frac{\pi}{180^{\circ}}\) instead of \(\frac{180^{\circ}}{\pi}\). Also, when you write an angle in degrees, you must use a degree symbol, and this answer choice does not have one. The correct answer is \(-150^{\circ}\).
Summary
Angles can be measured in two ways: with degrees and radians. Radian measure of a central angle is defined as the ratio of the arc length to the length of the radius. This definition leads to the arc length formula: \(s=r \theta\).
Radians and degrees are connected by the relationship \(360^{\circ}=2 \pi \text { radians }\). If you wish to convert from degrees to radians, multiply the degree measure by \(\frac{\pi}{180^{\circ}}\). If you wish to convert from radians to degrees, multiply the radian measure by \(\frac{180^{\circ}}{\pi}\).


