7.4: Choosing a Priority List
- Page ID
- 34214
We will explore two algorithms for selecting a priority list.
Decreasing time algorithm
The decreasing time algorithm takes the approach of trying to get the very long tasks out of the way as soon as possible by putting them first on the priority list.
Create the priority list by listing the tasks in order from longest completion time to shortest completion time.
Consider the scheduling problem represented by the digraph below. Create a priority list using the decreasing time list algorithm, then use it to schedule for two processors using the list processing algorithm.
Solution
To use the decreasing time list algorithm, we create our priority list by listing the tasks in order from longest task time to shortest task time. If there is a tie, we will list the task with smaller task number first (not for any good reason, but just for consistency).
For this digraph, the decreasing time algorithm would create a priority list of:
\(\mathrm{T}_{6}(10), \mathrm{T}_{3}(7), \mathrm{T}_{10}(7), \mathrm{T}_{1}(6), \mathrm{T}_{5}(5), \mathrm{T}_{4}(4), \mathrm{T}_{7}(4), \mathrm{T}_{2}(3), \mathrm{T}_{8}(3), \mathrm{T}_{9}(2)\)
Once we have the priority list, we can create the schedule using the list processing algorithm. With two processors, we’d get:
Time 0: We identify ready tasks, and assign \(\mathrm{T}_{3}\) to \(\mathrm{P}_{1}\) and \(\mathrm{T}_{1}\) to \(\mathrm{P}_{2}\)
Priority list: \(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \cancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, (\mathrm{T}_{4}), \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

Time 6: \(\mathrm{P}_{2}\) completes \(\mathrm{T}_{1}\). No new tasks become ready, so \(\mathrm{T}_{4}\) is assigned to \(\mathrm{P}_{2}\).
Priority list: \(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

Time 7: \(\mathrm{P}_{1}\) completes \(\mathrm{T}_{3}\). No new tasks become ready, so \(\mathrm{T}_{2}\) is assigned to \(\mathrm{P}_{1}\).
Priority list: \(\mathrm{T}_{6}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \cancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Time 10: Both processors complete their tasks. \(\mathrm{T}_{6}\) becomes ready, and is assigned to \(\mathrm{P}_{1}\). No other tasks are ready, so \(\mathrm{P}_{2}\) idles.
Priority list: \(\cancel{\mathrm{T}_{6}}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \xcancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Time 20: With \(\mathrm{T}_{6}\) complete, \(\mathrm{T}_{5}\) and \(\mathrm{T}_{7}\) become ready, and are assigned to \(\mathrm{P}_{1}\) and \(\mathrm{P}_{2}\) respectively.
Priority list: \(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \cancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \cancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Time 24: \(\mathrm{P}_{2}\) completes \(\mathrm{T}_{7}\). No new items become ready, so \(\mathrm{P}_{2}\) idles.
Time 25: \(\mathrm{P}_{1}\) completes \(\mathrm{T}_{5}\). \(\mathrm{T}_{8}\) and \(\mathrm{T}_{9}\) become ready, and are assigned.
Priority list: \(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \cancel{(\mathrm{T}_{8})}, \cancel{(\mathrm{T}_{9})}\)

Time 27: \(\mathrm{T}_{9}\) is completed. No items ready, so \(\mathrm{P}_{2}\) idles.
Time 28: \(\mathrm{T}_{8}\) is completed. \(\mathrm{T}_{10}\) becomes ready, and is assigned to \(\mathrm{P}_{1}\).
Priority list: \(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \cancel{(\mathrm{T}_{10})}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \xcancel{(\mathrm{T}_{8})}, \xcancel{(\mathrm{T}_{9})}\)

This is our completed schedule, with a finishing time of 35.
Using the decreasing time algorithm, the priority list led to a schedule with a finishing time of 35. Is this good? It certainly looks like there was a lot of idle time in this schedule. To get some idea how good or bad this schedule is, we could compute the critical time, the minimum time to complete the job. To find this, we look for the sequence of tasks with the highest total completion time. For this digraph that sequence would appear to be: \(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) with total sequence time of 28. From this we can conclude that our schedule isn’t horrible, but there is a possibility that a better schedule exists.
Determine the priority list for the digraph from Try it Now 1 using the decreasing time algorithm.
- Answer
-
\(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4,} \mathrm{T}_{2}, \mathrm{T}_{9}, \mathrm{T}_{5}, \mathrm{T}_{3}, \mathrm{T}_{6,} \mathrm{T}_{8}\)
Critical path algorithm
A sequence of tasks in the digraph is called a path. In the previous example, we saw that the critical path dictates the minimum completion time for a schedule. Perhaps, then, it would make sense to consider the critical path when creating our schedule. For example, in the last schedule, the processors began working on tasks 1 and 3 because they were longer tasks, but starting on task 2 earlier would have allowed work to begin on the long task 6 earlier.
The critical path algorithm allows you to create a priority list based on idea of critical paths.
- Find the critical path.
- The first task in the critical path gets added to the priority list.
- Remove that task from the digraph
- Repeat, finding the new critical path with the revised digraph
The original digraph from Example 3 has critical path \(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) so \(\mathrm{T}_{2}\) gets added first to the priority list. Removing \(\mathrm{T}_{2}\) from the digraph, it now looks like:
Solution
The critical path (longest path) in the remaining digraph is now \(\mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) so \(\mathrm{T}_{6}\) is added to the priority list and removed.
Now there are two paths with the same longest length: \(\mathrm{T}_{1}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10}\) and \(\mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}\). We can add \(\mathrm{T}_{1}\) to the priority list (or \(\mathrm{T}_{3}\) – we usually add the one with smaller item number) and remove it, and continue the process.
I’m sure you can imagine that searching for the critical path every time you remove a task from the digraph would get really tiring, especially for a large digraph. In practice, the critical path algorithm is implementing by first working from the end backwards. This is called the backflow algorithm.
- Introduce an “end” vertex, and assign it a time of 0, shown in [brackets]
- Move backwards to every vertex that has an arrow to the end and assign it a critical time
- From each of those vertices, move backwards and assign those vertices critical times. Notice that the critical time for the earlier vertex will be that task’s time plus the critical time for the later vertex.
Example: Consider this segment of digraph.
In this case, if T2 has already been determined to have a critical time of 10, then T1 will have a critical time of 5+10 = 15
If you have already assigned a critical time to a vertex, replace it only if the new time is larger.
Example: In the digraph below, T1 should be labeled with a critical time of 16, since it is the longer of 5+10 and 5+11.
4. Repeat until all vertices are labeled with their critical times
One you have completed the backflow algorithm, you can easily create the critical path priority list by using the critical times you just found.
- Apply the backflow algorithm to the digraph
- Create the priority list by listing the tasks in order from longest critical time to shortest critical time
This version of the Critical Path Algorithm will usually be the easier to implement.
Applying this to our digraph from the earlier example, we start applying the backflow algorithm.
Solution
We add an end vertex and give it a critical time of 0.
We then move back to \(\mathrm{T}_{4}, \mathrm{T}_{9},\) and \(\mathrm{T}_{10}\), labeling them with their critical times
From each vertex marked with a critical time, we go back. \(\mathrm{T}_{7}\), for example, will get labeled with a critical time 11 – the task time of 4 plus the critical time of 7 for \(\mathrm{T}_{10}\). For \(\mathrm{T}_{5}\), there are two paths to the end. We use the longer, labeling T5 with critical time \(5+7 = 12\).
Continue the process until all vertices are labeled. Notice that the critical time for \(\mathrm{T}_{5}\) ended got replaced later with the even longer path through \(\mathrm{T}_{8}\).
We can now quickly create the critical path priority list by listing the tasks in decreasing order of critical time:
Priority list: \(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{4}, \mathrm{T}_{9}\)
Applying this priority list using the list processing algorithm, we get the schedule:

In this particular case, we were able to achieve the minimum possible completion time with this schedule, suggesting that this schedule is optimal. This is certainly not always the case.
Determine the priority list for the digraph from Try it Now 1 using the critical path algorithm.
- Answer
-
Applying the backflow algorithm, we get this:
The critical path priority list is: \(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{2}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{3}, \mathrm{T}_{6}\)
This example is designed to show that the critical path algorithm doesn’t always work wonderfully. Schedule the tasks in the digraph below on three processors using the critical path algorithm.
Solution
To create a critical path priority list, we could first apply the backflow algorithm:
This yields the critical-path priority list: \(\mathrm{T}_{1}, \mathrm{T}_{6}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{4}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{2}, \mathrm{T}_{3}\).
Applying the list processing algorithm to this priority list leads to the schedule:
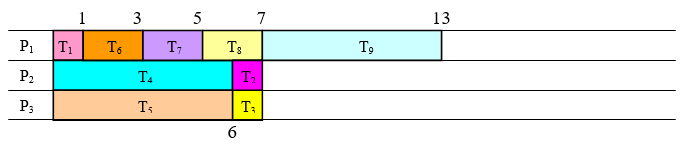
This schedule has finishing time of 13.
By observation, we can see that a much better schedule exists for the example above:

In most cases the critical path algorithm will lead to a very good schedule. There are cases, like this, where it will not. Unfortunately, there is no known algorithm to always produce the optimal schedule.


