14.4: The Development and Use of Different Number Bases

Introduction and Basics

During the previous discussions, we have been referring to positional base systems. In this section of the chapter, we will explore exactly what a base system is and what it means if a system is “positional.” We will do so by first looking at our own familiar, base-ten system and then deepen our exploration by looking at other possible base systems. In the next part of this section, we will journey back to Mayan civilization and look at their unique base system, which is based on the number 20 rather than the number 10.

A base system is a structure within which we count. The easiest way to describe a base system is to think about our own base-ten system. The base-ten system, which we call the “decimal” system, requires a total of ten different symbols/digits to write any number. They are, of course, 0, 1, 2, ….. 9.

The decimal system is also an example of a positional base system, which simply means that the position of a digit gives its place value. Not all civilizations had a positional system even though they did have a base with which they worked.

In our base-ten system, a number like 5,783,216 has meaning to us because we are familiar with the system and its places. As we know, there are six ones, since there is a 6 in the ones place. Likewise, there are seven “hundred thousands,” since the 7 resides in that place. Each digit has a value that is explicitly determined by its position within the number. We make a distinction between digit, which is just a symbol such as 5, and a number, which is made up of one or more digits. We can take this number and assign each of its digits a value. One way to do this is with a table, which follows:

\(\begin{array}{|l|l|l|l|}
\hline 5,000,000 & =5 \times 1,000,000 & =5 \times 10^{6} & \text { Five million } \\
\hline+700,000 & =7 \times 100,000 & =7 \times 10^{5} & \text { Seven hundred thousand } \\
\hline+80,000 & =8 \times 10,000 & =8 \times 10^{4} & \text { Eighty thousand } \\
\hline+3,000 & =3 \times 1000 & =3 \times 10^{3} & \text { Three thousand } \\
\hline+200 & =2 \times 100 & =2 \times 10^{2} & \text { Two hundred } \\
\hline+10 & =1 \times 10 & =1 \times 10^{1} & \text { Ten } \\
\hline+6 & =6 \times 1 & =6 \times 10^{0} & \text { Six } \\
\hline 5,783,216 & \text { Five million, seven hundred eighty-three thousand, two hundred sixteen } \\
\hline
\end{array}\)

From the third column in the table we can see that each place is simply a multiple of ten. Of course, this makes sense given that our base is ten. The digits that are multiplying each place simply tell us how many of that place we have. We are restricted to having at most 9 in any one place before we have to “carry” over to the next place. We cannot, for example, have 11 in the hundreds place. Instead, we would carry 1 to the thousands place and retain 1 in the hundreds place. This comes as no surprise to us since we readily see that 11 hundreds is the same as one thousand, one hundred. Carrying is a pretty typical occurrence in a base system.

However, base-ten is not the only option we have. Practically any positive integer greater than or equal to 2 can be used as a base for a number system. Such systems can work just like the decimal system except the number of symbols will be different and each position will depend on the base itself.

Other Bases

For example, let’s suppose we adopt a base-five system. The only modern digits we would need for this system are 0,1,2,3 and 4. What are the place values in such a system? To answer that, we start with the ones place, as most base systems do. However, if we were to count in this system, we could only get to four (4) before we had to jump up to the next place. Our base is 5, after all! What is that next place that we would jump to? It would not be tens, since we are no longer in base-ten. We’re in a different numerical world. As the base-ten system progresses from 10⁰ to10¹, so the base-five system moves from 5⁰ to 5¹ = 5. Thus, we move from the ones to the fives.

After the fives, we would move to the 5² place, or the twenty fives. Note that in base-ten, we would have gone from the tens to the hundreds, which is, of course, 10².

Let’s take an example and build a table. Consider the number 30412 in base five. We will write this as 30412₅ , where the subscript 5 is not part of the number but indicates the base we’re using. First off, note that this is NOT the number “thirty thousand, four hundred twelve.” We must be careful not to impose the base-ten system on this number. Here’s what our table might look like. We will use it to convert this number to our more familiar base-ten system.

\(\begin{array}{|l|l|l|l|}
\hline & \text { Base 5 } & \text { This column coverts to base-ten } & \text { In Base-Ten } \\
\hline & 3 \times 5^{4} & =3 \times 625 & =1875 \\
\hline+ & 0 \times 5^{3} & =0 \times 125 & =0 \\
\hline+ & 4 \times 5^{2} & =4 \times 25 & =100 \\
\hline+ & 1 \times 5^{1} & =1 \times 5 & =5 \\
\hline+ & 2 \times 5^{0} & =2 \times 1 & =2 \\
\hline & & \text { Total } & 1982 \\
\hline
\end{array}\)

As you can see, the number 30412₅ is equivalent to 1,982 in base-ten. We will say \(30412_{5}=1982_{10}\). All of this may seem strange to you, but that’s only because you are so used to the only system that you’ve ever seen.

Example 3

Convert \(6234_{7}\) to a base 10 number.

Solution

We first note that we are given a base-7 number that we are to convert. Thus, our places will start at the ones ( \(7^{0}\) ), and then move up to the \(7^{\prime} s, 49^{\prime} s\left(7^{2}\right),\) etc. Here's the breakdown:

\(\begin{array}{|l|l|l|l|}
\hline & \text { Base 7 } & \text { Convert } & \text { Base 10 } \\
\hline & =6 \times 7^{3} & =6 \times 343 & =2058 \\
\hline+ & =2 \times 7^{2} & =2 \times 49 & =98 \\
\hline+ & =3 \times 7 & =3 \times 7 & =21 \\
\hline+ & =4 \times 1 & =4 \times 1 & =4 \\
\hline & & \text { Total } & 2181 \\
\hline
\end{array}\)

\( \text { Thus } 6234_{7}=2181_{10} \)

Try it Now 3

Convert \(41065_7\) to a base 10 number.

Answer

\(41065_{7}=9994_{10}\)

Converting from Base 10 to Other Bases

Converting from an unfamiliar base to the familiar decimal system is not that difficult once you get the hang of it. It’s only a matter of identifying each place and then multiplying each digit by the appropriate power. However, going the other direction can be a little trickier. Suppose you have a base-ten number and you want to convert to base-five. Let’s start with some simple examples before we get to a more complicated one.

Example 4

Convert twelve to a base-five number.

Solution

We can probably easily see that we can rewrite this number as follows:

\[12=(2 \times 5)+(2 \times 1) \nonumber \]

Hence, we have two fives and 2 ones. Hence, in base-five we would write twelve as \(22_{5}\). Thus, \(12_{10}=22_{5}\)

Example 5

Convert sixty-nine to a base-five number.

Solution

We can see now that we have more than 25, so we rewrite sixty-nine as follows:

\[69=(2 \times 25)+(3 \times 5)+(4 \times 1)  \nonumber \]

Here, we have two twenty-fives, 3 fives, and 4 ones. Hence, in base five we have 234 . Thus, \(69_{10}=234_5\)

Example 6

Convert the base-seven number \(3261_{7}\) to base 10

Solution

The powers of 7 are:

\[\begin{array}{l}
7^{0}=1 \\
7^{1}=7 \\
7^{2}=49 \\
7^{3}=343
\end{array} \nonumber\]

Etc...

\[3261_{7}=(3 \times 343)+(2 \times 49)+(6 \times 7)+(1 \times 1)=1170_{10} \nonumber \]

Thus \(3261_{7}=1170_{10}\)

Try it Now 4

Convert 143 to base 5

Answer

\(143_{10}=1033_{5}\)

Try it Now 5

Convert the base-three number \(21021_{3}\) to base 10.

Answer

\(21021_{3}=196_{10}\)

In general, when converting from base-ten to some other base, it is often helpful to determine the highest power of the base that will divide into the given number at least once. In the last example, \(5^{2}=25\) is the largest power of five that is present in \(69,\) so that was our starting point. If we had moved to \(5^{3}=125\), then 125 would not divide into 69 at least once.

Converting from Base 10 to Base \(b\)

1. Find the highest power of the base b that will divide into the given number at least once and then divide.
2. Write down the whole number part, then use the remainder from division in the next step.
3. Repeat step two, dividing by the next highest power of the base b, writing down the whole number part (including 0), and using the remainder in the next step.
4. Continue until the remainder is smaller than the base. This last remainder will be in the “ones” place.
5. Collect all your whole number parts to get your number in base \(b\) notation.

Example 7

Convert the base-ten number 348 to base-five.

Solution

The powers of five are:

\(\begin{array}{l}
5^{0}=1 \\
5^{1}=5 \\
5^{2}=25 \\
5^{3}=125 \\
5^{4}=625
\end{array}\)

Etc..

since \(348\) is smaller than \(625,\) but bigger than \(125,\) we see that \(5^{3}=125\) is the highest power of five present in \(348 .\) So we divide 125 into 348 to see how many of them there are:

\(348 \div 125=2\) with remainder 98

We write down the whole part, 2, and continue with the remainder. There are 98 left over, so we see how many 25’s (the next smallest power of five) there are in the remainder:

\(98 \div 25=3\) with remainder 23

We write down the whole part, 2, and continue with the remainder. There are 23 left over, so we look at the next place, the 5’s:

\(23 \div 5=4\) with remainder 3

This leaves us with 3, which is less than our base, so this number will be in the “ones” place. We are ready to assemble our base-five number:

\( 348=\left(2 \times 5^{3}\right)+\left(3 \times 5^{2}\right)+\left(4 \times 5^{1}\right)+(3 \times 1) \)

Hence, our base-five number is \(2343 .\) We'll say that \(348_{10}=2343_{5}\)

Example 8

Convert the base-ten number 4509 to base-seven.

Solution

The powers of 7 are:

\(\begin{array}{l}
7^{0}=1 \\
7^{1}=7 \\
7^{2}=49 \\
7^{3}=343 \\
7^{4}=2401 \\
7^{5}=16807
\end{array}\)

Etc…

The highest power of 7 that will divide into 4509 is \(7^{4}=2401\)

With division, we see that it will go in 1 time with a remainder of \(2108 .\) So we have 1 in the \(7^{4}\) place.

The next power down is \(7^{3}=343,\) which goes into 2108 six times with a new remainder of \(50 .\) So we have 6 in the \(7^{3}\) place.

The next power down is \(7^{2}=49\), which goes into 50 once with a new remainder of \(1 .\) So there is a 1 in the \(7^{2}\) place.

The next power down is \(7^{1}\) but there was only a remainder of \(1,\) so that means there is a 0 in the 7 's place and we still have 1 as a remainder.

That, of course, means that we have 1 in the ones place.

\(\begin{array}{ll}
4509 \div 7^{4}= & 1 \quad \mathrm{R} \quad 2108 \\
2108 \div 7^{3}= & 6 \quad \mathrm{R} \quad 50 \\
50 \div 7^{2}= & 1 \quad \mathrm{R} \quad 1 \\
1 \div 7^{1}= & 0 \quad \mathrm{R} \quad 1 \\
1 \div 7^{0}= & 1 \\
4509_{10}=16101_7
\end{array}\)

Putting all of this together means that \(4509_{10}=16101_{7}\)

Try it Now 6

Convert \(657_{10}\) to a base 4 number.

Answer

\(657_{10}=22101_{4}\)

Try it Now 7

Convert \(8377_{10}\) to a base 8 number.

Answer

\(8377_{10}=20271_{8} \)

Another Method For Converting From Base 10 to Other Bases

As you read the solution to this last example and attempted the “Try it Now” problems, you may have had to repeatedly stop and think about what was going on. The fact that you are probably struggling to follow the explanation and reproduce the process yourself is mostly due to the fact that the non-decimal systems are so unfamiliar to you. In fact, the only system that you are probably comfortable with is the decimal system.

As budding mathematicians, you should always be asking questions like “How could I simplify this process?” In general, that is one of the main things that mathematicians do…they look for ways to take complicated situations and make them easier or more familiar. In this section we will attempt to do that.

To do so, we will start by looking at our own decimal system. What we do may seem obvious and maybe even intuitive but that’s the point. We want to find a process that we readily recognize works and makes sense to us in a familiar system and then use it to extend our results to a different, unfamiliar system.

Let's start with the decimal number, \(4863_10\). We will convert this number to base \(10 .\) Yeah, I know it's already in base \(10,\) but if you carefully follow what we're doing, you'll see it makes things work out very nicely with other bases later on. We first note that the highest power of 10 that will divide into 4863 at least once is \(10^{3}=1000 .\) In general, this is the first step in our new process; we find the highest power that a given base that will divide at least once into our given number.

We now divide 1000 into 4863:

\[4863 \div 1000=4.863\nonumber \]

This says that there are four thousands in 4863 (obviously). However, it also says that there are 0.863 thousands in 4863. This fractional part is our remainder and will be converted to lower powers of our base (10). If we take that decimal and multiply by 10 (since that’s the base we’re in) we get the following:

\[0.863 \times 10=8.63\nonumber \]

Why multiply by 10 at this point? We need to recognize here that 0.863 thousands is the same as 8.63 hundreds. Think about that until it sinks in.

\[(0.863)(1000)=863\nonumber \]

\[(8.63)(100)=863\nonumber \]

These two statements are equivalent. So, what we are really doing here by multiplying by 10 is rephrasing or converting from one place (thousands) to the next place down (hundreds).

\[0.863 \times 10 \Rightarrow 8.63\nonumber \]

\[\text{(Parts of Thousands) }\times 10 \Rightarrow \text{ Hundreds}\nonumber \]

What we have now is 8 hundreds and a remainder of 0.63 hundreds, which is the same as 6.3 tens. We can do this again with the 0.63 that remains after this first step.

\[0.63 \times 10 \Rightarrow 6.3\nonumber \]

\[\text{Hundreds } \times 10 \Rightarrow \text{ Tens}\nonumber \]

So we have six tens and 0.3 tens, which is the same as 3 ones, our last place value.

Now here’s the punch line. Let’s put all of the together in one place:

Note that in each step, the remainder is carried down to the next step and multiplied by 10, the base. Also, at each step, the whole number part, which is circled, gives the digit that belongs in that particular place. What is amazing is that this works for any base! So, to convert from a base 10 number to some other base, \(b\), we have the following steps we can follow:

Converting from Base 10 to Base \(b\): Another method

1. Find the highest power of the base \(b\) that will divide into the given number at least once and then divide.
2. Keep the whole number part, and multiply the fractional part by the base \(b\).
3. Repeat step two, keeping the whole number part (including 0), carrying the fractional part to the next step until only a whole number result is obtained.
4. Collect all your whole number parts to get your number in base \(b\) notation.

We will illustrate this procedure with some examples.

Example 9

Convert the base 10 number, \(348_{10}\), to base \(5 .\)

Solution

This is actually a conversion that we have done in a previous example. The powers of five are:

\(\begin{array}{l}
5^{0}=1 \\
5^{1}=5 \\
5^{2}=25 \\
5^{3}=125 \\
5^{4}=625
\end{array}\)

Etc…

The highest power of five that will go into 348 at least once is \(5^{3}\)

We divide by 125 and then proceed.

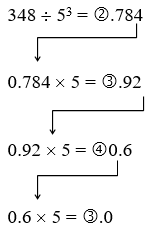
By keeping all the whole number parts, from top bottom, gives 2343 as our base 5 number. Thus, \(2343_{5}=348_{10}\)

We can compare our result with what we saw earlier, or simply check with our calculator, and find that these two numbers really are equivalent to each other.

Example 10

Convert the base 10 number, \(3007_{10}\), to base 5.

Solution

The highest power of 5 that divides at least once into 3007 is \(5^{4}=625 .\) Thus, we have:

\(\begin{array}{l}
3007 \div 625=(4).8112 \\
0.8112 \times 5=(4).056 \\
0.056 \times 5=(0).28 \\
0.28 \times 5=(1)0.4 \\
0.4 \times 5=(2)0.0
\end{array}\)

This gives us that \(3007_{10}=44012_{5} .\) Notice that in the third line that multiplying by 5 gave us 0 for our whole number part. We don't discard that! The zero tells us that a zero in that place. That is, there are no \(5^{2}\) 's in this number

This last example shows the importance of using a calculator in certain situations and taking care to avoid clearing the calculator’s memory or display until you get to the very end of the process.

Example 11

Convert the base 10 number, \(63201_{10}\), to base 7.

Solution

The powers of 7 are:

\(\begin{array}{l}
7^{0}=1 \\
7^{1}=7 \\
7^{2}=49 \\
7^{3}=343 \\
7^{4}=2401 \\
7^{5}=16807
\end{array}\)

etc…

The highest power of 7 that will divide at least once into 63201 is \(7^{5}\). When we do the initial division on a calculator, we get the following:

\(63201 \div 7^{5}=3.760397453\)

The decimal part actually fills up the calculators display and we don’t know if it terminates at some point or perhaps even repeats down the road. So if we clear our calculator at this point, we will introduce error that is likely to keep this process from ever ending. To avoid this problem, we leave the result in the calculator and simply subtract 3 from this to get the fractional part all by itself. DO NOT ROUND OFF! Subtraction and then multiplication by seven gives:

\(63201 \div 7^{5}=(3).760397453\)
\(0.760397453 \times 7=(5).322782174\)
\(0.322782174 \times 7=(2).259475219\)
\(0.259475219 \times 7=(1).816326531\)
\(0. 816326531 \times 7=(5).714285714\)
\(0.714285714 \times 7=(5).000000000\)

Yes, believe it or not, that last product is exactly 5, as long as you don’t clear anything out on your calculator. This gives us our final result: \(63201_{10}=352155_{7}\).

If we round, even to two decimal places in each step, clearing our calculator out at each step along the way, we will get a series of numbers that do not terminate, but begin repeating themselves endlessly. (Try it!) We end up with something that doesn’t make any sense, at least not in this context. So be careful to use your calculator cautiously on these conversion problems.

Also, remember that if your first division is by \(7^{5}\), then you expect to have 6 digits in the final answer, corresponding to the places for \(7^{5}, 7^{4}\) and so on down to \(7^{0}\). If you find yourself with more than 6 digits due to rounding errors, you know something went wrong

Try it Now 8

Convert the base 10 number, \(9352_{10}\), to base 5.

Answer

\(9352_{10}=244402_{5}\)

Try it Now 9

Convert the base 10 number, 1500_{10}, to base 3.

Be careful not to clear your calculator on this one. Also, if you’re not careful in each step, you may not get all of the digits you’re looking for, so move slowly and with caution.

Answer

\( 1500_{10}=2001120_{3} \)