17.11: Forms of Valid Arguments
- Page ID
- 41411
Rather than making a truth table for every argument, we may be able to recognize certain common forms of arguments that are valid (or invalid). If we can determine that an argument fits one of the common forms, we can immediately state whether it is valid or invalid.
The law of detachment applies when a conditional and its antecedent are given as premises, and the consequent is the conclusion. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & p \\ \text{Conclusion:} & q \end{array}\)
The Latin name, modus ponens, translates to “mode that affirms”.
Recall this argument from an earlier example:
\(\begin{array} {ll} \text{Premise:} & \text{If you bought bread, then you went to the store.} \\ \text{Premise:} & \text{You bought bread.} \\ \text{Conclusion:} & \text{You went to the store.} \end{array}\)
In symbolic form:
\(\begin{array} {ll} \text{Premise:} & b \rightarrow s \\ \text{Premise:} & b \\ \text{Conclusion:} & s \end{array}\)
This argument has the structure described by the law of detachment. (The second premise and the conclusion are simply the two parts of the first premise detached from each other.) Instead of making a truth table, we can say that this argument is valid by stating that it satisfies the law of detachment.
The law of contraposition applies when a conditional and the negation of its consequent are given as premises, and the negation of its antecedent is the conclusion. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim q \\ \text{Conclusion:} & \sim p \end{array}\)
The Latin name, modus tollens, translates to “mode that denies”.
Notice that the second premise and the conclusion look like the contrapositive of the first premise, \(\sim q \rightarrow \sim p\), but they have been detached. You can think of the law of contraposition as a combination of the law of detachment and the fact that the contrapositive is logically equivalent to the original statement.
\(\begin{array} {ll} \text{Premise:} & \text{If I drop my phone into the swimming pool, my phone will be ruined.} \\ \text{Premise:} & \text{My phone isn’t ruined.} \\ \text{Conclusion:} & \text{I didn’t drop my phone into the swimming pool.} \end{array}\)
If we let \(d=\mathrm{I}\) drop the phone in the pool and \(r=\) the phone is ruined, then we can represent the argument this way:
\(\begin{array} {ll} \text{Premise:} & d \rightarrow r \\ \text{Premise:} & \sim r \\ \text{Conclusion:} & \sim d \end{array}\)
The form of this argument matches what we need to invoke the law of contraposition, so it is a valid argument.
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{Your toothbrush is dry.} \\ \text{Conclusion:} & \text{You didn’t brush your teeth before bed.} \end{array}\)
- Answer
-
Let \(b=\) brushed teeth and \(w=\) toothbrush is wet.
\(\begin{array} {ll} \text{Premise:} & b \rightarrow w \\ \text{Premise:} & \sim w \\ \text{Conclusion:} & \sim b \end{array}\)
This argument is valid by the Law of Contraposition.
The transitive property has as its premises a series of conditionals, where the consequent of one is the antecedent of the next. The conclusion is a conditional with the same antecedent as the first premise and the same consequent as the final premise. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \rightarrow r \\ \text{Conclusion:} & p \rightarrow r \end{array}\)
The earlier example about buying a shirt at the mall is an example illustrating the transitive property. It describes a chain reaction: if the first thing happens, then the second thing happens, and if the second thing happens, then the third thing happens. Therefore, if we want to ignore the second thing, we can say that if the first thing happens, then we know the third thing will happen. We don’t have to mention the part about buying jeans; we can simply say that the first event leads to the final event. We could even have more than two premises; as long as they form a chain reaction, the transitive property will give us a valid argument.
\(\begin{array} {ll} \text{Premise:} & \text{If a soccer player commits a reckless foul, she will receive a yellow card.} \\ \text{Premise:} & \text{If Hayley receives a yellow card, she will be suspended for the next match.} \\ \text{Conclusion:} & \text{If Hayley commits a reckless foul, she will be suspended for the next match.} \end{array}\)
If we let \(r=\) committing a reckless foul, \(y=\) receiving a yellow card, and \(s=\) being suspended, then our argument looks like this:
\(\begin{array} {ll} \text{Premise:} & r \rightarrow y \\ \text{Premise:} & y \rightarrow s \\ \text{Conclusion:} & r \rightarrow s \end{array}\)
This argument has the exact structure required to use the transitive property, so it is a valid argument.
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{If the old lady swallows a fly, she will swallow a spider.} \\ \text{Premise:} & \text{If the old lady swallows a spider, she will swallow a bird.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\\text{Premise:} & \text{If the old lady swallows a bird, she will swallow a cat.} \\ \text{Premise:} & \text{If the old lady swallows a cat, she will swallow a dog.} \\\text{Premise:} & \text{If the old lady swallows a dog, she will swallow a goat.} \\ \text{Premise:} & \text{If the old lady swallows a goat, she will swallow a cow.} \\ \text{Premise:} & \text{If the old lady swallows a cow, she will swallow a horse.} \\ \text{Premise:} & \text{If the old lady swallows a horse, she will die, of course.} \\ \text{Conclusion:} & \text{If the old lady swallows a fly, she will die, of course.} \end{array}\)
- Answer
-
This argument is valid by the Transitive Property, which can involve more than two premises, as long as they continue the chain reaction. The premises \(f \rightarrow s, s \rightarrow b, b \rightarrow c, c \rightarrow d\) \(d \rightarrow g, g \rightarrow w, w \rightarrow h, h \rightarrow x\) can be reduced to \(f \rightarrow x. \) (Because we had already used \(c\) and \(d\) we decided to use \(w\) for cow and \(x\) for death. If the old lady swallows the fly, she will eventually eat a horse and die.
In a disjunctive syllogism, the premises consist of an or statement and the negation of one of the options. The conclusion is the other option. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \vee q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & q \end{array}\)
The order of the two parts of the disjunction isn't important. In other words, we could have the premises \(p \vee q\) and \(\sim q,\) and the conclusion \(p\)
\(\begin{array} {ll} \text{Premise:} & \text{I can either drive or take the train.} \\ \text{Premise:} & \text{I refuse to drive.} \\ \text{Conclusion:} & \text{I will take the train.} \end{array}\)
If we let \(d=I\) drive and \(t=I\) take the train, then the symbolic representation of the argument is:
\(\begin{array} {ll} \text{Premise:} & d \vee t \\ \text{Premise:} & \sim d \\ \text{Conclusion:} & t \end{array}\)
This argument is valid because it has the form of a disjunctive syllogism. I have two choices, and one of them is not going to happen, so the other one must happen.
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{Alison was required to write a 10-page paper or give a 5-minute speech.} \\ \text{Premise:} & \text{Alison did not give a 5-minute speech.} \\ \text{Conclusion:} & \text{Alison wrote a 10-page paper.} \end{array}\)
- Answer
-
Let \(p=\) wrote a paper and \(s=\) gave a speech.
\(\begin{array} {ll} \text{Premise:} & p \vee s \\ \text{Premise:} & -s \\ \text{Conclusion:} & p \end{array}\)
This argument is valid by Disjunctive Syllogism. Alison had to do one or the other; she didn’t choose the speech, so she must have chosen the paper.
Keep in mind that, when you are determining the validity of an argument, you must assume that the premises are true. If you don’t agree with one of the premises, you need to keep your personal opinion out of it. Your job is to pretend that the premises are true and then determine whether they force you to accept the conclusion. You may attack the premises in a court of law or a political discussion, of course, but here we are focusing on the structure of the arguments, not the truth of what they actually say.
We have just looked at four forms of valid arguments; there are two common forms that represent invalid arguments, which are also called fallacies.
The fallacy of the converse arises when a conditional and its consequent are given as premises, and the antecedent is the conclusion. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \\ \text{Conclusion:} & p \end{array}\)
Notice that the second premise and the conclusion look like the converse of the first premise, \(q \rightarrow p\), but they have been detached. The fallacy of the converse incorrectly tries to assert that the converse of a statement is equivalent to that statement.
\(\begin{array} {ll} \text{Premise:} & \text{If I drink coffee after noon, then I have a hard time falling asleep that night.} \\ \text{Premise:} & \text{I had a hard time falling asleep last night.} \\ \text{Conclusion:} & \text{I drank coffee after noon yesterday.} \end{array}\)
If we let \(c=\mathrm{I}\) drink coffee after noon and \(h=\mathrm{I}\) have a hard time falling asleep, then our argument looks like this:
\(\begin{array} {ll} \text{Premise:} & c \rightarrow h \\ \text{Premise:} & h \\ \text{Conclusion:} & c \end{array}\)
This argument uses converse reasoning, so it is an invalid argument. There could be plenty of other reasons why I couldn’t fall asleep: I could be worried about money, my neighbors might have been setting off fireworks, …
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{If you pull that fire alarm, you will get in big trouble.} \\ \text{Premise:} & \text{You got in big trouble.} \\ \text{Conclusion:} & \text{You must have pulled the fire alarm.} \end{array}\)
- Answer
-
Let \(f=\) pulled fire alarm and \(t=\) got in big trouble.
\(\begin{array} {ll} \text{Premise:} & f \rightarrow t \\ \text{Premise:} & t \\ \text{Conclusion:} & f \end{array}\)
The fallacy of the inverse occurs when a conditional and the negation of its antecedent are given as premises, and the negation of the consequent is the conclusion. The general form is:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & \sim q \end{array}\)
Again, notice that the second premise and the conclusion look like the inverse of the first premise, \(\sim p \rightarrow \sim q\), but they have been detached. The fallacy of the inverse incorrectly tries to assert that the inverse of a statement is equivalent to that statement.
\(\begin{array} {ll} \text{Premise:} & \text{If you listen to the Grateful Dead, then you are a hippie.} \\ \text{Premise:} & \text{Sky doesn’t listen to the Grateful Dead.} \\ \text{Conclusion:} & \text{Sky is not a hippie.} \end{array}\)
If we let \(g=\) listen to the Grateful Dead and \(h=\) is a hippie, then this is the argument:
\(\begin{array} {ll} \text{Premise:} & g \rightarrow h \\ \text{Premise:} & \sim g \\ \text{Conclusion:} & \sim h \end{array}\)
This argument is invalid because it uses inverse reasoning. The first premise does not imply that all hippies listen to the Grateful Dead; there could be some hippies who listen to Phish instead.
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{If a hockey player trips an opponent, he will be assessed a 2-minute penalty.} \\ \text{Premise:} & \text{Alexei did not trip an opponent.} \\ \text{Conclusion:} & \text{Alexei will not be assessed a 2-minute penalty.} \end{array}\)
- Answer
-
Let \(t=\) tripped and \(p=\) got a penalty.
\(\begin{array} {ll} \text{Premise:} & t \rightarrow p \\ \text{Premise:} & \sim t \\ \text{Conclusion:} & \sim p \end{array}\)
This argument is invalid because it has the form of the Fallacy of the Inverse. Alexei may have gotten a penalty for an infraction other than tripping.
Of course, arguments are not limited to these six basic forms; some arguments have more premises, or premises that need to be rearranged before you can see what is really happening. There are plenty of other forms of arguments that are invalid. If an argument doesn’t seem to fit the pattern of any of these common forms, though, you may want to use a Venn diagram or a truth table instead.
Lewis Carroll, author of Alice’s Adventures in Wonderland, was a math and logic teacher, and wrote two books on logic. In them, he would propose premises as a puzzle, to be connected using syllogisms. The following example is one such puzzle.
Solve the puzzle. In other words, find a logical conclusion from these premises.
All babies are illogical.
Nobody is despised who can manage a crocodile.
Illogical persons are despised.
Let \(b=\) is a baby, \(d=\) is despised, \(i=\) is illogical, and \(m=\) can manage a crocodile.
Then we can write the premises as:
\(b \rightarrow i\)
\(m \rightarrow \sim d\)
\(i \rightarrow d\)
Writing the second premise correctly can be a challenge; it can be rephrased as “If you can manage a crocodile, then you are not despised.”
Using the transitive property with the first and third premises, we can conclude that \(b \rightarrow d\), that all babies are despised. Using the contrapositive of the second premise, \(d \rightarrow \sim m\), we can then use the transitive property with \(b \rightarrow d\) to conclude that \(b \rightarrow \sim m\), that babies cannot manage crocodiles. While it is silly, this is a logical conclusion from the given premises.
\(\begin{array} {ll} \text{Premise:} & \text{If I work hard, I’ll get a raise.} \\ \text{Premise:} & \text{If I get a raise, I’ll buy a boat.} \\ \text{Conclusion:} & \text{If I don’t buy a boat, I must not have worked hard.} \end{array}\)
If we let \(h=\) working hard, \(r=\) getting a raise, and \(b=\) buying a boat, then we can represent our argument symbolically:
\(\begin{array} {ll} \text{Premise:} & h \rightarrow r \\ \text{Premise:} & r \rightarrow b \\ \text{Conclusion:} & \sim b \rightarrow \sim h \end{array}\)
Using the transitive property with the two premises, we can conclude that \(h \rightarrow b\), if I work hard, then I will buy a boat. When we learned about the contrapositive, we saw that the conditional statement \(h \rightarrow b\) is equivalent to \(\sim b \rightarrow \sim h\). Therefore, the conclusion is indeed a logical syllogism derived from the premises.
Is this argument valid?
\(\begin{array} {ll} \text{Premise:} & \text{If I go to the party, I’ll be really tired tomorrow.} \\ \text{Premise:} & \text{If I go to the party, I’ll get to see friends.} \\ \text{Conclusion:} & \text{If I don’t see friends, I won’t be tired tomorrow.} \end{array}\)
- Answer
-
Let \(p=\) go to party, \(t=\) be tired, and \(f=\) see friends.
\(\begin{array} {ll} \text{Premise:} & p \rightarrow t \\ \text{Premise:} & p \rightarrow f \\ \text{Conclusion:} & -f \rightarrow \sim t \end{array}\)
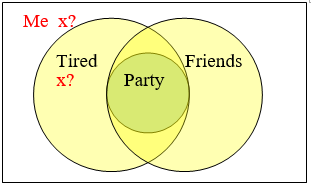 We could try to rewrite the second premise using the contrapositive to state \(\sim f \rightarrow \sim p\), but that does not allow us to form a syllogism. If I don’t see friends, then I didn’t go the party, but that is not sufficient to claim I won’t be tired tomorrow. Maybe I stayed up all night watching movies.
We could try to rewrite the second premise using the contrapositive to state \(\sim f \rightarrow \sim p\), but that does not allow us to form a syllogism. If I don’t see friends, then I didn’t go the party, but that is not sufficient to claim I won’t be tired tomorrow. Maybe I stayed up all night watching movies.A Venn diagram can help, if we set it up correctly. The “party” circle must be completely contained within the intersection of the other circles. We know that I am somewhere outside the “friends” circle, but we cannot determine whether I am in the “tired” circle. All we really know for sure is that I didn’t go to the party.


