4.4: Adding and Subtracting Fractions

Last updated
Save as PDF

Page ID: 9845

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Here are two very similar fractions: $\frac{2}{7}$ and $\frac{3}{7}$. What might it mean to add them? It might seem reasonable to say:

\[\frac{2}{7}\; \text{represents 2 pies shared by 7 kids} \ldotp \nonumber \]

\[\frac{3}{7}\; \text{represents 3 pies shared by 7 kids} \ldotp \nonumber \]

So maybe $\frac{2}{7} + \frac{3}{7}$ represents 5 pies among 14 kids, giving the answer $\frac{5}{14}$. It is very tempting to say that “adding fractions” means “adding pies and adding kids.”

The trouble is that a fraction is not a pie, and a fraction is not a child. So adding pies and adding children is not actually adding fractions. A fraction is something different. It is related to pies and kids, but something more subtle. A fraction is an amount of pie per child.

One cannot add pies, one cannot add children. One must add instead the amounts individual kids receive.

Example: 2/7 + 3/7

Let us take it slowly. Consider the fraction $\frac{2}{7}$. Here is a picture of the amount an individual child receives when two pies are given to seven kids:

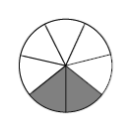
$two-sevenths.png$

Consider the fraction $\frac{3}{7}$. Here is the picture of the amount an individual child receives when three pies are given to seven children:

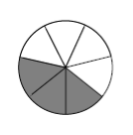
$three-sevenths.png$

The sum $\frac{2}{7} + \frac{3}{7}$ corresponds to the sum:

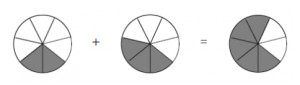
$sum-of-five-sevenths-300x85.png$

The answer, from the picture, is $\frac{5}{7}$.

Think / Pair / Share

Remember that $\frac{5}{7}$ means “the amount of pie that one child gets when five pies are shared by seven children.” Carefully explain why that is the same as the picture given by the sum above:

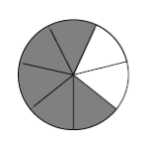
$five-sevenths.png$

Your explanation should use both words and pictures!

Most people read this as “two sevenths plus three sevenths gives five sevenths” and think that the problem is just as easy as saying “two apples plus three apples gives five apples.” And, in the end, they are right!

$sum-of-five-sevenths-300x85.png$

This is how the addition of fractions is first taught to students: Adding fractions with the same denominator seems just as easy as adding apples:

4 tenths + 3 tenths + 8 tenths = 15 tenths.

\[\frac{4}{10} + \frac{3}{10} + \frac{8}{10} = \frac{15}{10} \ldotp \nonumber \]

(And, if you like, $\frac{15}{10} = \frac{5 \cdot 3}{5 \cdot 2} = \frac{3}{2}$.)

82 sixty-fifths + 91 sixty-fifths = 173 sixty-fifths:

\[\frac{82}{65} + \frac{91}{65} = \frac{173}{65} \ldotp \nonumber \]

We are really adding amounts per child not amounts, but the answers match the same way.

We can use the “Pies Per Child Model” to explain why adding fractions with like denominators works in this way.

Example: 2/7 + 3/7

Think about the addition problem $\frac{2}{7} + \frac{3}{7}$:

\[\begin{split} \text{amount of pie each kids gets when 7 kids share 2 pies} & \\ +\; \text{amount of pie each kids gets when 7 kids share 3 pies} \\ \hline ????? \qquad \qquad \qquad \qquad & \end{split} \nonumber \]

Since in both cases we have 7 kids sharing the pies, we can imagine that it is the same 7 kids in both cases. First, they share 2 pies. Then they share 3 more pies. The total each child gets by the time all the pie-sharing is done is the same as if the 7 kids had just shared 5 pies to begin with. That is:

\[\begin{split} \text{amount of pie each kids gets when 7 kids share 2 pies} & \\ +\; \text{amount of pie each kids gets when 7 kids share 3 pies} \\ \hline \text{amount of pie each kids gets when 7 kids share 5 pies} \ldotp & \end{split} \nonumber \]

\[\frac{2}{7} + \frac{3}{7} = \frac{5}{7} \ldotp \nonumber \]

Now let us think about the general case. Our claim is that

\[\frac{a}{d} + \frac{b}{d} = \frac{a + b}{d} \ldotp \nonumber \]

Translating into our model, we have $d$ kids. First, they share $a$ pies between them, and $\frac{a}{d}$ represents the amount each child gets. Then they share $b$ more pies, so the additional amount of pie each child gets is $\frac{b}{d}$. The total each kid gets is $\frac{a}{d} + \frac{b}{d}$.

But it does not really matter that the kids first share $a$ pies and then share $b$ pies. The amount each child gets is the same as if they had started with all of the pies — all $a + b$ of them — and shared them equally. That amount of pie is represented by $\frac{a + b}{d}$.

Think / Pair / Share

How can you subtract fractions with the same denominator? For example, what is $$\frac{400}{903} - \frac{170}{903} ?$$
Use the “Pies Per Child” model to carefully explain why $$\frac{a}{d} - \frac{b}{d} = \frac{a - b}{d} \ldotp$$
Explain why the fact that the denominators are the same is essential to this addition and subtraction method. Where is that fact used in the explanations?

Fractions with Different Denominators

This approach to adding fractions suddenly becomes tricky if the denominators involved are not the same common value. For example, what is $\frac{2}{5} + \frac{1}{3}$?

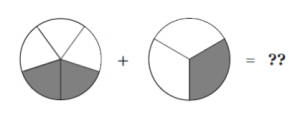
$two-fifths-plus-one-third-300x123.png$

Let us phrase this question in terms of pies and kids:

Suppose Poindexter is part of a team of five kids that shares two pies. Then later he is part of a team of three kids that shares one pie. How much pie does Poindexter receive in total?

Think / Pair / Share

Talk about these questions with a partner before reading on. It is actually a very difficult problem! What might a student say, if they do not already know about adding fractions? Write down any of your thoughts.

Do you see that this is the same problem as computing $\frac{2}{5} + \frac{1}{3}$?
What might be the best approach to answering the problem?

One way to think about answering this addition question is to write $\frac{2}{5}$ in a series of alternative forms using our key fraction rule (that is, multiply the numerator and denominator each by 2, and then each by 3, and then each by 4, and so on) and to do the same for $\frac{1}{3}$:

\[\begin{split} \frac{2}{5} + \frac{1}{3} & \\ \frac{4}{10} \quad \frac{2}{6} & \\ \textcolor{red}{\frac{6}{15}} \quad \frac{3}{9} & \\ \frac{8}{20}\; \; \frac{4}{12} & \\ \frac{10}{25}\; \; \textcolor{red}{\frac{5}{15}} & \\ \vdots \qquad \vdots\; & \end{split} \nonumber \]

We see that the problem $\frac{2}{5} + \frac{1}{3}$ is actually the same as $\frac{6}{15} + \frac{5}{15}$. So we can find the answer using the same-denominator method:

\[\frac{2}{5} + \frac{1}{3} = \frac{6}{15} + \frac{5}{15} = \frac{11}{15} \ldotp \nonumber \]

Example: 3/8 + 3/10

Here is another example of adding fractions with unlike denominators: $\frac{3}{8} + \frac{3}{10}$. In this case, Valerie is part of a group of 8 kids who share 3 pies. Later she is part of a group of 10 kids who share 3 different pies. How much total pie did Valerie get?

\[\begin{split} \frac{3}{8} + \frac{3}{10} & \\ \frac{6}{16}\; \; \frac{6}{20} & \\ \frac{9}{24}\; \; \frac{9}{30} & \\ \frac{12}{32}\; \; \textcolor{red}{\frac{12}{40}} & \\ \textcolor{red}{\frac{15}{40}}\; \; \frac{15}{50} & \\ \vdots \qquad \vdots\; & \end{split} \nonumber \]

\[\frac{3}{8} + \frac{3}{10} = \frac{15}{40} + \frac{12}{40} = \frac{17}{40} \ldotp \nonumber \]

Of course, you do not need to list all of the equivalent forms of each fraction in order to find a common denominator. If you can see a denominator right away (or think of a faster method that always works), go for it!

Think / Pair / Share

Cassie suggests the following method for the example above:

When the denominators are the same, we just add the numerators. So when the numerators are the same, shouldn’t we just add the denominators? Like this: \[\frac{3}{8} + \frac{3}{10} = \frac{3}{18} \ldotp \nonumber \]

What do you think of Cassie’s suggestion? Does it make sense? What would you say if you were Cassie’s teacher?

On Your Own

Try these exercises on your own. For each addition exercise, also write down a “Pies Per Child” interpretation of the problem. You might also want to draw a picture.

What is $\frac{1}{2} + \frac{1}{3}$?
What is $\frac{2}{5} + \frac{37}{10}$?
What is $\frac{1}{2} + \frac{3}{10}$?
What is $\frac{2}{3} + \frac{5}{7}$?
What is $\frac{1}{2} + \frac{1}{4} + \frac{1}{8}$?
What is $\frac{3}{10} + \frac{4}{25} + \frac{7}{20} + \frac{3}{5} + \frac{49}{50}$?

Now try these subtraction exercises.

What is $\frac{7}{10} - \frac{3}{10}$?
What is $\frac{7}{10} - \frac{3}{20}$?
What is $\frac{1}{3} - \frac{1}{5}$?
What is $\frac{2}{35} - \frac{2}{7} + \frac{2}{5}$?
What is $\frac{1}{2} - \frac{1}{4} - \frac{1}{8} - \frac{1}{16}$?