8.2: Primes and GCF
- Page ID
- 70329
You will need: Centimeter Strips (Material Cards 16A-16L)
Prime Number Squares (Material Cards 19A-19B)
Composite Number Squares (Material Cards 20A-20B)
In these first few exercises, you'll be using C-strips to explore divisors, factors, prime numbers and composite numbers.
a. Take out the Hot Pink (H) C-strip. Use your C-strips (one color at a time) to see if you can form a train made up of C-strips of the same color equal in length to the hot pink C-strip in other words, see if you can do it with all whites (always possible for any train length), or all reds, or all light greens, etc. You should be able to make six different trains each train is made up of a single color. Draw a picture of each of these trains under the Hot Pink one shown. I've drawn two trains for you already one is simply the hot pink strip (a train consisting of just one C-strip), and a second is made up of three purple C-strips.
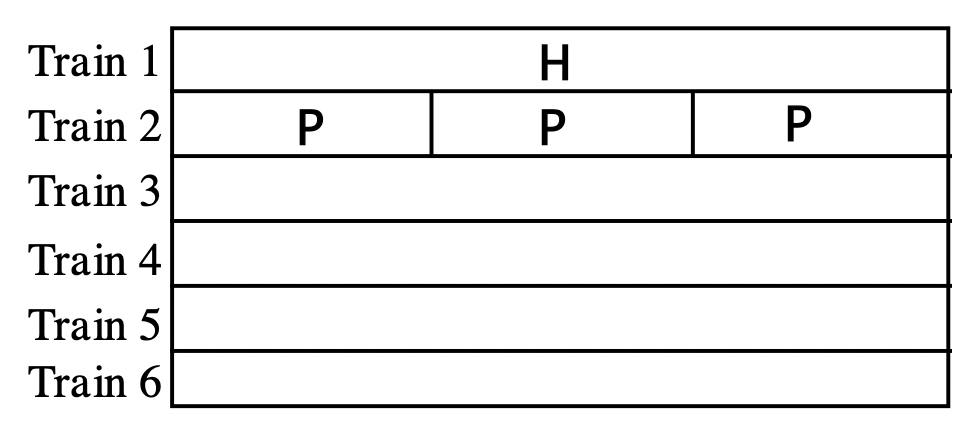
b. Take each train and form it into a rectangle. Then, find a C-strip that fits across the width of the rectangle, which is the top if the C-strips of the train made into a rectangle are placed vertically. From this, you should be able to tell from which multiplication problem each train was formed. From this information, write an equation using C-strips and then translate to an equation with numbers. For instance, for train 2, first I would make a rectangle out of the three purple C-strips. Next, I would try to find a C-strip to fit across the top, which would be light green. Therefore, train 2 was formed from the multiplication \(L \times P\): remember that since the train is formed with purple C-strips, P is the second letter in the multiplication. So, the equation in C-strips is \(L \times P = H\), and the numerical equivalent is \(3 \times 4 = 12\). Follow this same procedure for the other four trains you made in part a.
Train 1 illustrates the multiplication \(W \times H = H\), or \(1 \times 12 = 12\). (Note that if the hot pink strip is placed vertically, the white C-strip fits across the top.)
Train 2 illustrates the multiplication \(L \times P = H\), or \(3 \times 4 = 12\).
Train 3 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = 12.
Train 4 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
Train 5 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
Train 6 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
In exercise part 1b, the set of numbers placed in the blanks before the equal sign in the equations with numbers are called factors or divisors of 12. Note, that because of the commutative property of multiplication, each factor or divisor was listed twice.
c. List the numbers that are factors of 12 (length of the hot pink C-strip). Only list each number once.
Use the same procedure used in exercise 1 to make all possible rectangles from a train having each of the following lengths. Use the C-strip(s) shown in the parenthesis to make a train having the given length. Then, after discovering the possible rectangles that can be made, list the factors (the actual numbers) of each number. Every number greater than 1 has at least two factors.
| a. Factors of 2 (red C-strip): ____ |
| b. Factors of 3 (light green C-strip): ____ |
| c. Factors of 4 (purple C-strip): ____ |
| d. Factors of 5 (yellow C-strip): ____ |
| e. Factors of 6 (dark green C-strip): ____ |
| f. Factors of 7 (black C-strip): ____ |
| g. Factors of 8 (brown C-strip): ____ |
| h. Factors of 9 (blue C-strip): ____ |
| i. Factors of 10 (orange C-strip): ____ |
| j. Factors of 11 (silver C-strip): ____ |
| k. Factors of 13 (brown + yellow): ____ |
| l. Factors of 14 (orange + purple): ____ |
| m. Factors of 15 (black + brown): ____ |
| n. Factors of 16 (blue + black): ____ |
a. List the numbers from exercise 2 that have exactly 2 factors: _____
b. What do you notice about the 2 factors each of these number have? Is there a pattern or anything they have in common with each other?
c. List numbers from exercise 2 that have an odd number (3 or 5) of factors: _____
d. What do all of these numbers have in common?
Definition: A whole number that has exactly two different factors is called a prime number.
If a number is prime, its only factors are 1 and itself. In other words, if a number, p, is prime, its only factors are 1 and p. If you are using the C-strips and try to make a rectangle out of a train that has a length that is a prime number, the only possibility is when the width is 1 and the length is the length of the original train. That is because those are the only factors, and no other number divides into it.
NOTE: 1 is NOT prime since it doesn't have two different factors it only has one 1.
Definition: Any whole number larger than 1 that is not prime is called a composite number.
The whole numbers, 0 and 1, are neither prime nor composite. Any whole number larger than 1 is either prime or composite.
If a number is composite, it means that it has more than 2 factors, and can be written as a product of factors less than itself. For instance, 12 is not a prime number. It can be written as 2 \(\cdot\) 6 or 3 \(\cdot\) 4. This is called factoring, and \(2 \cdots 6\) and \(3 \cdots 4\) are only two ways of factoring 12.
Get out your prime number squares and composite number squares. If you haven't already done so, color the prime number squares so that each prime number has a different color the 2's could be yellow, the 3's could be blue, the 5's could be green, the 7's could be purple, the 11's could be red, the 13's could be orange, the 17's could be pink, and so on. All of the composite number squares should remain white.
What we are going to do is factor numbers. Anytime we have a white number, we know it is composite and can be factored further. The ultimate goal will be to factor numbers into a product of primes, which means there will only be colored squares to represent each number.
Let's begin by factoring 12. Take out a white number square that says 12, and put it in front of you. Since it is white, it can be factored into a product of two smaller numbers. Someone might choose 3 and 4; another might choose 2 and 6. Replace 12 with the two squares you chose. For 12, it so happens that no matter which combination of two numbers you choose, one of the squares you choose will be colored, which means it is prime and can't be factored (or broken down) any further. But the other square will be white. Replace the white one with two other number squares by using smaller factors. In your pile, instead of a 12, you should have three squares, a 2, a 2 and a 3. There is no order it's just a group of three squares that if multiplied together represent 12. Below are two paths one might have taken to come up with the final solution. The arrows show one step after the other.
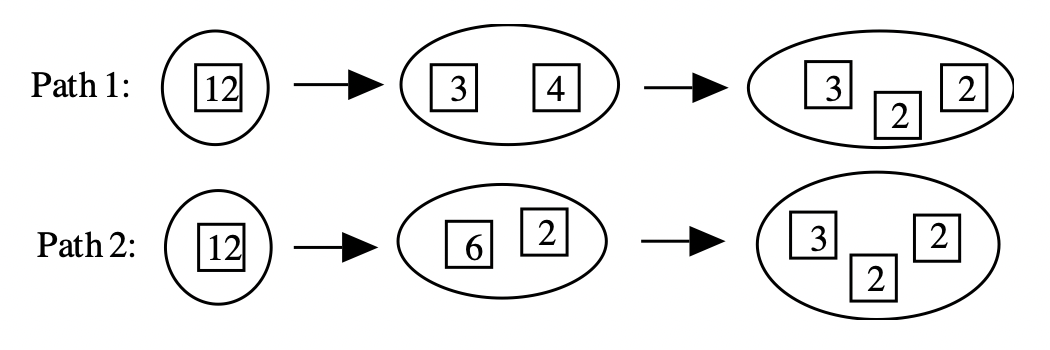
In the first path, the 12 was replaced with 3 and 4, and then the 4 was replaced with two 2's. In the second path, the 12 was replaced with a 6 and a 2, and then the 6 was replaced with a 2 and a 3. Using this model to prime factor, the numbers you end up should all be prime, and the understanding is that when the final (prime) factors are MULTIPLIED together, we obtain the original number we tried to factor. In other words, the prime factorization for 12 is \(3 \cdot 2 \cdot 2\). Because of the commutative and associative properties of multiplication, the order of the factors is insignificant. Sometimes, for consistency, the factors are written in ascending or descending order, but this is not necessary unless you are instructed to write it in a particular order. If you are asked to write the prime factorization of 12, you might write \(12 = 2 \cdot 2 \cdot 3\) (or \(12 = 2^{2} \cdot 3\)). To check, multiply the prime factors to make sure that the product really is the number you set out to prime factor. For large numbers, you should use a calculator. Here is another way to show on paper the replacement process going on for factoring 12 using the number squares.
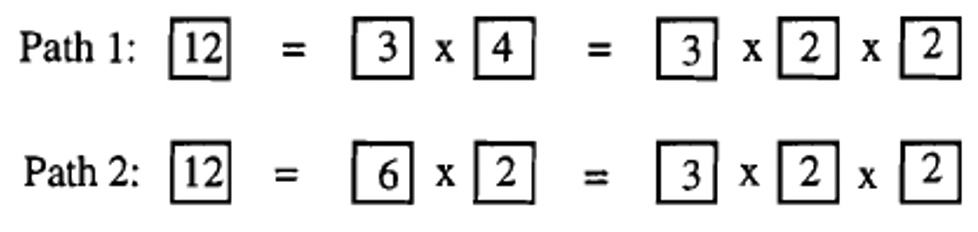
Example: Use the number squares to prime factor 210, and show the individual steps.
Note: Since there is not a number square for 210, write 210 on a blank square to begin.
Solution 1: \(210 = 21 \cdots 10 = 3 \cdots 7 \cdots 2 \cdots 5\)
Solution 2: \(210 = 3 \cdots 70 = 2 \cdots 105 = 2 \cdots 3 \cdots 35 = 2 \cdots 3 \cdots 5 \cdots 7\)
Solution 3: \(210 = 30 \cdots 7 = 5 \cdots 6 \cdots 7 = 5 \cdots 2 \cdots 3 \cdots 7\)
There are many other ways one might go about factoring 210, but in the end, there are 4 prime factors that when multiplied together equal 210. Because of the commutative and associative properties of multiplication, \(3 \cdots 7 \cdots 2 \cdots 5 = 2 \cdots 3 \cdots 5 \cdots 7 = 5 \cdots 2 \cdots 3 \cdots 7\). Usually, the primes are written in ascending order (from the smallest factor to the largest factor. We write that the prime factorization of 210 is \(2 \cdots 3 \cdots 5 \cdots 7\).
This leads to a very important theorem. You can think of the prime numbers as building blocks for all whole numbers greater than 1. Every whole number greater than 1 is prime, or it can be expressed as the product of prime factors (called the prime factorization). The fact that any composite number can be written as a unique product of primes is so important that it is called the Fundamental Theorem of Arithmetic.
The Fundamental Theorem of Arithmetic:
Every composite number has exactly one unique prime factorization (except for the order in which you write the factors.)
Note again that the order in which the factors are written doesn't matter. However, for consistency, they are usually written in ascending order (from smallest to largest). Also, exponents may be used if a factor is repeated in the prime factorization. For instance, the prime factorization of 12 is usually written as \(2 \cdots 2 \cdots 3\) or \(2^{2} \cdots 3\)
Use the number squares to prime factor each of the following composite numbers into a product of primes. Write the prime factorization so the factors are written in ascending order (from smallest to largest). None of these numbers is prime. Show each of the individual steps one at a time, not just the final product.
| a. 45 = _____ |
| b. 65 = _____ |
| c. 200 = _____ |
| d. 91 = _____ |
| e. 76 = _____ |
| f. 350 = _____ |
| g. 189 = _____ |
| h. 74 = _____ |
| i. 512 = _____ |
| j. 147 = _____ |
There are other methods commonly used to find the prime factorization. One uses a FACTOR TREE, which is similar to what you did with the prime and composite number squares. The difference is that it is done on paper, as opposed to using manipulatives. The number you are trying to factor is called the root, and is at the top. So, it's actually an upside down tree. If a number is not prime, you draw two branches down from that number and factor it as the product of any two factors. At the end of each branch is a smaller factor, which is called a leaf. If a leaf is prime, circle it, it is one of the factors in the prime factorization of the number. Otherwise, branch off again. When all of the leaves are circled prime numbers, you are done. The prime factorization of the root is the product of the leaves. Below is one way we factored 12, on the previous page, using squares.

Here are the individual steps showing how one might use a factor tree to factor 12, similar to how it was factored using the squares, via Path 1. Note the similarity.
|
Step 1: Factor 12 as 3d4 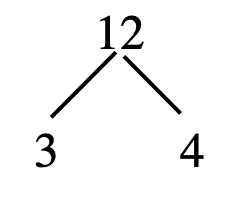 |
Step 2: Circle 3 since it is prime 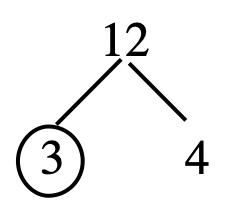 |
Step 3 Circle the 2s since they are prime 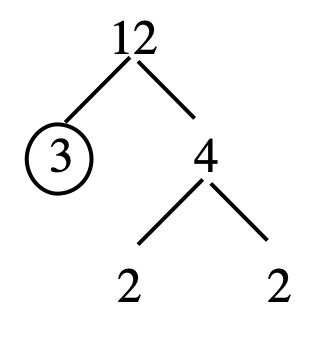 |
Step 4: Circle the 2s since they are prime 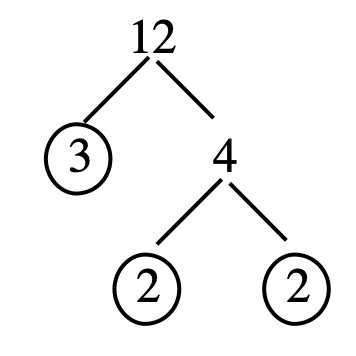 |
Step 5: The prime factorization of 12 is the product of the circled leaves 3 d2 d2 |
Below is the other way we factored 12 using squares.
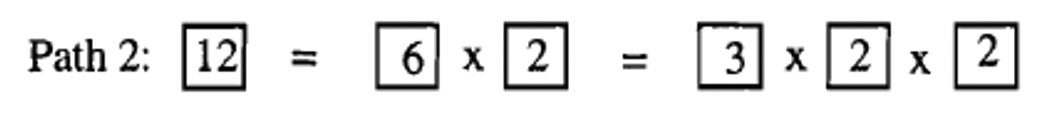
Here are the individual steps showing how one might use a factor tree to factor 12, similar to how it was factored using the squares, via Path 2. Again, note the similarity.
|
Step 1: Facrtor 12 as \(6 \times 2\) 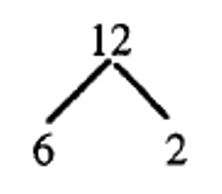 |
Step 2: Circle 2 since it is prime 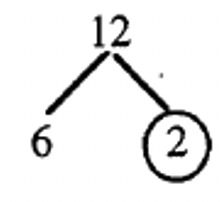 |
Step 3: Factor 6 as \(2 \times 3\) 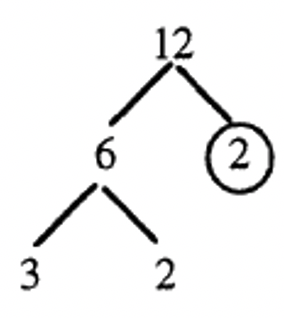 |
Step 4: Circle 3 and 2 since they are both prime. 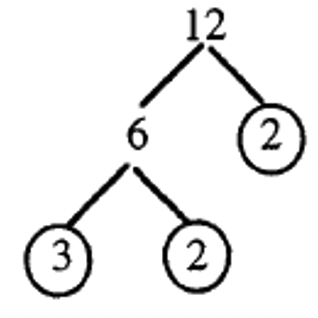 |
Step 5: The prime factorization of 12 is the product of the circled leaves \(3 \cdots 2 \cdots 2\) |
If you aren't sure whether a number is prime or composite and don't know how to start factoring, use the divisibility tests. See if it is possible to divide by 2, 3, 5, 7, 11, etc. Make sure there are no factors before you circle it and decide it's prime. You are going to repeat exercise 4 again, but this time, use a factor tree.
Use a factor tree to factor each of the following composite numbers into a product of primes. Write the prime factorization so the factors are written in ascending order (from smallest to largest). None of these numbers is prime. Show the individual steps. Show the factor tree under each problem.
| a. 45 = _____ | c. 200 = _____ |
| b. 65 = _____ | d. 91 = _____ |
| e. 76 = _____ | h. 74 = _____ |
| f. 350 = _____ | i. 512 = _____ |
| g. 189 = _____ | j. 147 = _____ |
The problem with trying to find the prime factorization is that sometimes it isn't obvious if a number you are trying to factor is prime or not. For instance, it is not immediately obvious whether or not 517 is prime or composite. This is where divisibility tests come in handy. Actually, if you want to find the prime factorization of 517, you only need to check if 517 has any prime numbers as factors. You'll need to try one prime at a time. Before going on, let's list the first several prime numbers starting with 2. Note: 2 is the only even prime number. To make a list, start with 2, 3, 5, and check to see if the next odd number is prime or not. It is not prime if one of the prime numbers listed earlier is a factor.
List all of the prime numbers less than 100. You only need to use the divisibility tests for 2, 3, 5 and 7 at the most to check if any odd number less than 100 is prime. In other words, any composite number less than 100 has 2, 3, 5 or 7 as a factor. We'll discuss why after this exercise.
Consider the possible ways to factor 54 as a product of 2 factors:
\(1 \cdots 54\), \(2 \cdots 27\), \(3 \cdots 18\), \(6 \cdots 9\), \(9 \cdots 6\), \(18 \cdots 3\), \(27 \cdots 2\), \(54 \cdots 1\)
Note that if you start with the smallest factor (1) as the left factor, you start repeating half-way through the list. This "half-way" mark happens after you get to the square root of the number you are factoring. The square root of 54 is between 7 and 8. So if you list a factor bigger than 7, it would have shown up earlier in the list as a factor less than 7. So that means if I am trying to find the prime factorization of 54, I only need to check prime numbers up to and including at most 7.
So why does any composite number less than 100 have 2, 3, 5 or 7 as a factor? The next prime number after 7 is 11. Since \(11^{2}\), or 121, is greater than 100, if there was a prime number greater than or equal to 11 that was a factor of a number less than 100, then the other factor would have to be less than 11. Think about it. If both factors were bigger than 11, the product would be more than 121! This realization makes finding the prime factorization of a number much easier. This is how it works.
Since \(3^{2} = 9\), any composite number < 9 has 2 as a factor.
Since \(5^{2} = 25\), any composite number < 25 has 2 or 3 as a factor.
Since \(7^{2} = 49\), any composite number < 49 has 2, 3 or 5 as a factor.
Since \(11^{2} = 121\), any composite number < 121 has 2, 3, 5 or 7 as a factor.
Since \(13^{2} = 169\), any composite number < 169 has 2, 3, 5, 7 or 11 as a factor.
Since \(17^{2} = 289\), any composite number < 289 has 2, 3, 5, 7, 11 or 13 as a factor.
Since \(19^{2} = 361\), any composite number < 361 has 2, 3, 5, 7, 11, 13 or 17 as a factor.
Since \(23^{2} = 529\), any composite number < 529 has 2, 3, 5, 7, 11, 13, 17 or 19 as a factor.
Now, we'll verify that some of the above statements are true.
Since \(3^{2} = 9\), any composite number < 9 has 2 as a factor.
This can be verified by listing the composite numbers less than 9 and showing that 2 is a factor of each of those numbers: the only composite numbers less than 9 are 4, 6, and 8. Verify that 2 is a factor of each of these numbers: \(4 = 2 \cdots 2, 6 = 2 \cdots 3, 8 = 2 \cdots 4\)
Since \(5^{2} = 25\), any composite number < 25 has 2 or 3 as a factor.
The previous example verified that the composite numbers less than 9 have 2 or 3 as a factor (since we've shown they all have 2 as a factor). So we only need to list and verify that the composite numbers less than 25 have 2 or 3 as a factor. The only composite numbers between 9 and 25 are 10, 12, 14, 15, 16, 18, 20, 21, 22, and 24. Mentally verify that 2 or 3 is a factor of each of these numbers. Note: each number only needs to have 2 OR 3 as a factor, although it may have both. For instance, 2 is a factor of 10, 3 is a factor of 15, and both 2 and 3 are factors of 18. You only have to make sure at least one of those factors is a factor of each composite number.
Since \(7^{2} = 49\), any composite number < 49 has 2, 3 or 5 as a factor. List the composite numbers between 25 and 49, and mentally verify that 2, 3, or 5 is a factor of each of these numbers.
Since \(11^{2} = 121\), any composite number < 121 has 2, 3, 5 or 7 as a factor. List the composite numbers between 49 and 121, and mentally verify that 2, 3, 5 or 7 is a factor of each of these numbers.
It gets tedious trying to verify for larger numbers, but the pattern continues. In other words, if you listed all of the composite numbers less than 361, which is \(19^{2}\), then you could actually verify that every one of them has 2, 3, 5, 7, 11 or 13 as a factor.
So, to find if 517 is prime or composite, since 517 is less than \(23^{2}\), I only need to check if any of the following are factors: 2, 3, 5, 7, 11, 13, 17 or 19. Instead of checking every number up to 517, only these eight need to be checked. You can use divisibility tests for the first five primes, then use a calculator for the last three. If you find a factor early on, there is no need to keep going.
Find the prime factorization of 517. Do this by using the divisibility tests up to 11, if necessary. If you still don't find a factor of 517, use a calculator to see if 13, 17 or 19 is a factor. Write the prime factorization here:
Because I wrote the squares of the first several prime numbers on the previous page, I knew I didn't have to check any primes higher than 19. One way to figure out the highest prime number you might have to check is to take the square root of the number you are trying to prime factor.
On your calculator, find the square root of 517 rounded to the nearest tenth:
You should have gotten 22.7. This tells us 517 is not a perfect square. Next, we know that if 517 is composite, it must have a prime factor less than 22.7. So, we need to determine the highest whole number that is prime that is less than 22.7. Start with 22 not prime; then 21 not prime; then 20 not prime; then 19 prime! Therefore, we at most need to check the primes up to 17: 2, 3, 5, 7, 11, 13, 17 and 19. When you actually prime factored 517, did you notice 11 was a factor? Did you use the divisibility test for 11?
So, \(517 = 11 \cdots 47\). Then, you look at the other factor, 47, and note it is prime, so you are done! By the way, 5 is the highest prime you'd have to check to see if 47 is prime!
What we have just described is a theorem called the Prime Factor Test. This is the formal way of stating that theorem.
Prime Factor Test: To test for prime factors of a number n, one need only search for prime factors p of n, where \(p^{2} \leq n\) ( or \(p \leq \sqrt{n}\))
For each number, determine the highest prime that might need to be checked to find the prime factorization of the number. Then, find the prime factorization. If it is prime, simply write the number itself, since that is the prime factorization.
|
a. 149 highest prime to check: _____ Prime factorization for 149: |
|
b. 273 highest prime to check: _____ Prime factorization for 149: |
|
c. 381 highest prime to check: _____ Prime factorization for 149: |
|
d. 437 highest prime to check: _____ Prime factorization for 149: |
|
e. 509 highest prime to check: _____ Prime factorization for 149: |
|
f. 613 highest prime to check: _____ Prime factorization for 149: |
|
g. 787 highest prime to check: _____ Prime factorization for 149: |
Now, let's look at a range of numbers and figure out how to determine which ones are prime. For instance, let's determine which numbers between 350 and 370 are prime. First of all, only odd numbers in this range are prime. So, begin by listing the odd numbers as possibilities: 351, 353, 355, 357, 359, 361, 363, 365, 367 and 369. Next, note 355 and 365 can't be prime since it is divisible by 5. Now, you might use the divisibility test for 3 to cross off 351, 357, 363 and 369 note you can cross of multiples of 3 by crossing off every third odd number if you start at a multiple of 3. Now, our list is down to these possibilities: 353, 359, 361, 367 and 369. The highest prime you'd have to check is the prime number that is less than the square root of 369, which is 19. So, simply check the rest of the primes (7, 11, 13, 17 and 19 at most) on each of these numbers to determine which, if any, are prime. 353 is prime; 359 is prime; 361 is 19, 367 is prime. Therefore, 353, 359 and 367 are the numbers between 350 and 370 that are prime. Furthermore, you should be able to write the prime factorization for all the numbers between 350 and 370 that are composite.
Find the prime factorization for all the numbers between 280 and 295. If a number is prime, simply write the number itself.
| a. 280 = ___________________ | i. 288 = ___________________ |
| b. 281 = ___________________ | j. 289 = ___________________ |
| c. 282 = ___________________ | k. 290 = ___________________ |
| d. 283 = ___________________ | l. 291 = ___________________ |
| e. 284 = ___________________ | m. 292 = ___________________ |
| f. 285 = ___________________ | n. 293 = ___________________ |
| g. 286 = ___________________ | o. 294 = ___________________ |
| h. 287 = ___________________ | p. 295 = ___________________ |
Twin primes are two consecutive odd numbers that are prime. For instance, 5 and 7 are twin primes, 11 and 13 are twin primes, 17 and 19 are twin primes. There is no pattern to determine how often twin primes come up. One unsolved question in mathematics is if there are a finite number of or infinitely many sets of twin primes. Nobody knows.
From your work in exercise 11, list any sets of twin primes: _____
Is it possible to have three odd numbers in a row that are prime? Why or why not?
One use of prime factoring a set of numbers is so you can find the greatest common factor (GCF) and least common multiple (LCM) of a set of numbers. Many people have trouble distinguishing between the greatest common factor and the least common multiple (LCM) because they don't think about what the words actually mean. The greatest common factor of a number is obviously a factor, but the adjective common describes that you want a factor that is common to all the numbers, and the adjective greatest describes that you want the very largest of the common factors of the numbers.
We are going to explore ways of finding the greatest common factor of two numbers, a and b. The notation to express this is GCF(a, b). It doesn't matter which number you list first in the parentheses – it's not an ordered pair. The greatest common factor of a set of numbers is the largest number that is a factor of each number.
We are going to explore different ways of finding the greatest common factor of two numbers.
First, we are going to explore one way to find the greatest common factor of 42 and 72.The notation to express this is GCF(42, 70). Remember: it doesn't matter which number you list first in the parentheses, it's not an ordered pair. GCF(42, 70) means the same thing as GCF(70, 42). The greatest common factor of 42 and 70 is the largest number that is a factor of both 42 and 70.
One way of doing this is to list every single factor of each number and then pick the biggest one that is a factor of each.
| a. List all of the factors of 42 in ascending order: ____ |
| b. List all of the factors of 70 in ascending order: ____ |
| c. List all of the factors that are common to both 42 and 70: ____ |
| d. List the greatest common factor of 42 and 70: ____ |
| e. Fill in the blank: GCF(42, 70) = ____ |
Listing all of the factors of a given number is sometimes a difficult task. For instance, it's easy to miss a factor. One remedy is to prime factor the number first. To list all of the factors of 42, one might first prime factor 42 like this: \(2 \cdots 3 \cdots 7\). For a number to be a factor of 42, it must be composed of the prime factors listed. Of course, 1 is always a factor. Next, you'd check 2, and then 3, which are both factors. 4 is not a factor because if it were, \(2 \cdots 2\) would be in the prime factorization! It's clear to see 5 is not a factor. 6 is a factor, since \(2 \cdots 3\) is in the prime factorization. Continuing on, 7 is a factor, but 8 is not because \(2 \cdots 2 \cdots 2\) is not in the prime factorization of 42. Neither is 9 \((3 \cdots 3), 10 (2 \cdots 5), 11, 12 (2 \cdots 2 \cdots 3)\), or 13. But 14 is a factor of 42 since \(2 \cdots 7\) is in the prime factorization. You can use this strategy as you check every number up to 42, but that is still a lot of numbers to check. Eventually, you'd get this list: 1, 2, 3, 6, 7, 14, 21, 42.
Here's a way to shorten the process a little more. Starting with the smallest factor 1, immediately list the other factor you'd have to multiply by that factor to get 42. So, we start with 1, 42. We check the next number, 2, and note it is a factor. To get the other factor that pairs up with 2, either divide 2 into 42, or simply look at the prime factorization of 42, with the 2 missing. There is \(3 \cdots 7\) left, which is the other factor. So the list is now 1, 42, 2, 21. Continuing, we note 3 is a factor. To get the other factor, either divide 42 by 3, or do it the easy way, which is to see what factors are left in the prime factorization of 42 with the 3 missing. Since there is a 2 and a 7, then the number that pairs up with 3 is 14.
The list is now 1, 42, 2, 21, 3, 14. Next, we note 4 and 5 are not factors. 6 is a factor since 2 and 3 (\(2 \cdots 3\)) is in the prime factorization. 7 is the number that pairs up with 6. So, the list is now: 1, 42, 2, 21, 3, 14, 6, 7. If you were to continue, the next number to check would be 7. Since \(7^{2}\) > 42, you can stop. All the factors that are larger than 7 will already be in the list because there would have been a smaller factor that it paired up with already. Now, put the list of factors of 42 in ascending order: 1, 2, 3, 6, 7, 14, 21, 42.
The same procedure can be used to list all the factors of 70. First, write the prime factorization of 70: \(2 \cdots 5 \cdots 7\). You would start off with 1 and 70: 1, 70. Next, it's clear 2 is a factor that pairs up with 35. The list is now: 1, 70, 2, 35. Next discard 3 and 4 as factors, and note 5 is a factor. The factors left are 2 and 7, which multiplied together is 14. So the list is 1, 70, 2, 35, 5, 14. Continuing on, note 6 is not a factor, and 7 is. 7 pairs up with 10. The list is now: 1, 70, 2, 35, 5, 14, 7, 10. Continuing on, note that 8 is not a factor. The next number to check would be 9. But \(9^{2}\) > 70, so all the factors higher are already in the list. Writing the list in ascending order, we get: 1, 2, 5, 7, 10, 14, 35, 70.
Make a note that in both of these examples, 42 and 70 each had exactly 3 prime numbers in the prime factorization. Consider the prime factorization of 220: \(2 \cdots 2 \cdots 5 \cdots 11\). Note that as you list factors, there may be one, two, or three other factors to multiply together to get the pair. 2 is a factor; its pair is \(2 \cdots 5 \cdots 11\), or 110. 4 \((2 \cdots 2\)) is a factor; its pair is 5 \(\cdots\) 11, or 55. 5 is a factor; its pair is \(2 \cdots 2 \cdots 11\), or 44. 10 (\(2 \cdots 5\)) is a factor; its pair is \(2 \cdot 11\), or 22. 11 is a factor; its pair is \(2 \cdots 2 \cdots 5\), or 20. As I check numbers larger than 11, I stop at 15 since 152 > 220. So, the list is: 1, 220, 2, 110, 4, 55, 5, 44, 10, 22, 11, 20. Writing these in ascending order, we get: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220.
By the way, it’s a lot more time-consuming for me to explain (and for you to read) how to list all the factors by prime factoring. But doing it is a lot easier! Now, do the next exercises. If you wish, use prime factorization to do parts a and b.
The goal of this problem is to find the greatest common factor of 92 and 115.
| a. List all of the factors of 92 in ascending order: |
| b. List all of the factors of 115 in ascending order: |
| c. List all of the factors that are common to both 92 and 115: |
| d. List the greatest common factor of 92 and 115: |
| e. Fill in the blank: GCF(92, 115) = |
The goal of this problem is to find the greatest common factor of 48, 54 and 63.
| a. List all of the factors of 48 in ascending order: |
| b. List all of the factors of 54 in ascending order: |
| c. List all of the factors of 63 in ascending order: |
| d. List all of the factors that are common to 48, 54 and also 63: |
| e. List the greatest common factor of 48, 54 and 63: |
| f. Fill in the blank: GCF(48, 54 and 63) = |
As you might have realized, listing factors can still be a very time-consuming way to find the greatest common factor, especially if the numbers are very large or have a lot of factors.
It's time to get out your colored prime number squares and white composite number squares again. We'll be using these to prime factor sets of numbers, which can then be used to find the greatest common factor of a set of numbers. This method is usually faster than the one we just used.
The goal of this next example is to find the greatest common factor of 42 and 72 using prime factorization with the prime and composite number squares.
Step 1: Use the squares to prime factor 42 and 72.
\(42 = 2 \cdots 3 \cdots 7\) and \(72 = 2 \cdots 2 \cdots 2 \cdots 3 \cdots 3\)
Step 2: Draw a line and put the prime factors of 42 above it. Next to that, draw a line and put the prime factors of 72 above it.
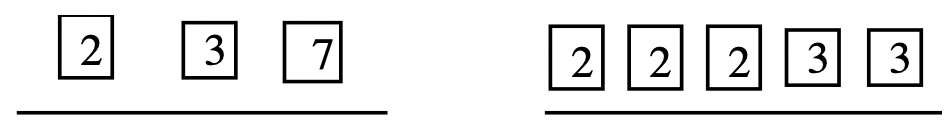
Step 3: Look at the prime factorization of the numbers. Move every factor they have in common under the line. They should have the same exact factors under the line, and they should have no common factors left above the line.
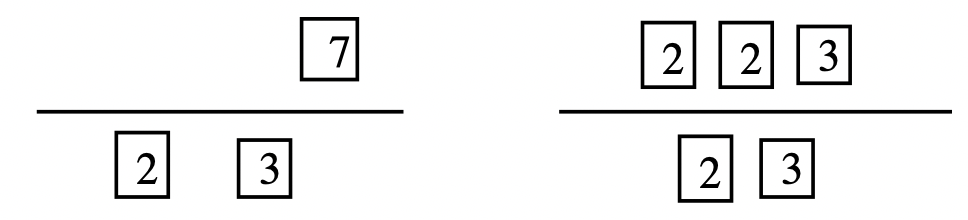
Step 4: The product of the factors under a line is the greatest common factor of the numbers. In this case, 2 \(\cdots\) 3, or 6, is the greatest common factor of 42 and 72.
Step 5: Use the correct notation to write the answer: GCF(42, 70) = 6.
This next example used the same steps to find the greatest common factor of 16, 24 and 36.
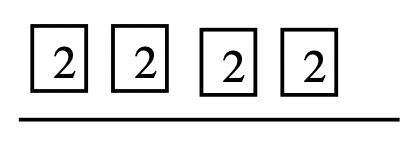
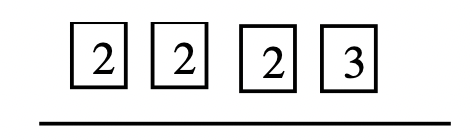
Step 1: Use the squares to prime factor 16, 24 and 36.
\(16 = 2 \cdots 2 \cdots 2 \cdots 2, 24 = 2 \cdots 2 \cdots 2 \cdots 3\) and \(36 = 2 \cdots 2 \cdots 3 \cdots 3\)
Step 2: Draw a line for each number and put the prime factors of each number above it.
 |
 |
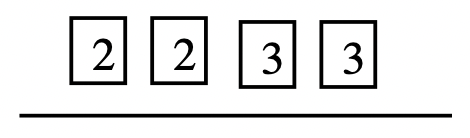 |
Step 3: Look at the prime factorization of the numbers. Move every factor that all three numbers have in common. There should be no factors left above the line that all three numbers have in common.
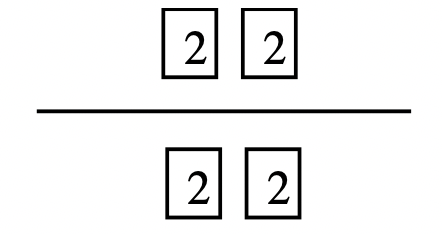 |
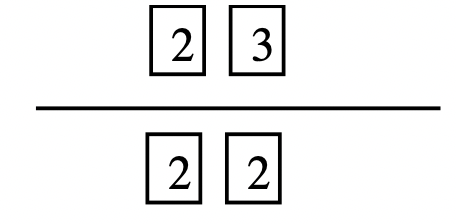 |
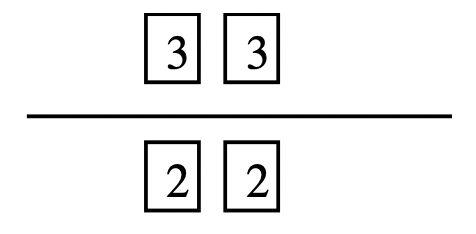 |
Step 4: The product of the factors under a line is the greatest common factor of the numbers. In this case, \(2 \cdots 2\), or 4, is the greatest common factor of 16, 24 and 36.
Step 5: Use the correct notation to write the answer: GCF(16, 24, 36) = 4.
Use the steps shown in the previous two examples to find the greatest common factor of each problem. Show a picture of how the problem looks at step 3 where the prime factorization of the greatest common factor is shown under the line of each number you first prime factored.
|
a. GCF(42, 70) = _____ (This answer should agree with Exercise 14e.) Show work below: |
|
b. GCF(92, 115) = _____ (This answer should agree with Exercise 15e.) Show work below: |
|
c. GCF(48, 54, 63) = _____ (This answer should agree with Exercise 16f.) Show work below: |
|
d. GCF(306, 340) = _____ Show work below: |
|
e. GCF(125, 275, 400) = _____ Show work below: |
|
f. GCF(126, 168, 210) = _____ Show work below: |
Let's say someone prime factored three large numbers, X, Y and Z like this:
| \(X = 2^{5} \cdots 3^{4} \cdots 7^{2} \cdots 11^{8} \cdots 13^{3}\) | \(Y = 2^{4} \cdots 3^{5} \cdots 5^{3} \cdots 7^{7} \cdots 13^{2}\) | \(Z = 2^{6} \cdots 3 \cdots 5^{5} \cdots 11^{3} \cdots 13^{4}\) |
a. State the prime factorization (exponential notation is okay) of the greatest common factor of X, Y and Z. GCF(X, Y, Z) =
b. Explain how you did part a.
One way to do the previous exercise is to begin by listing the common prime factors (without exponents) of X, Y and Z. They are 2, 3 and 13. So, as a start, write 2 \(\cdots\) 3 \(\cdots\) 13. Next, determine how many of each prime factor is common to X, Y and Z. Since X has 5 factors of 2, Y has 4 factors of 2, and Z has 6 factors of 2, they only have 4 factors of 2 in common. Similarly, they only have one factor of 3 in common, and 2 factors of 13 in common. Put these exponents on the factors and you've got the GCF of the three numbers: GCF(X, Y, Z) = \(2^{4} \cdots 3 \cdots 13^{2}\)
Did you notice that if you list the factors they have in common without exponents, you put on the smallest exponent they have in common for each prime?
Write the prime factorization of the greatest common factor of the set of numbers. For those that are factored with letters, assume each letter represents a different prime number.
|
a. If \(X = 2^{4} \cdots 3^{2} \cdots 7^{6} \cdots 11^{3} \cdots 13^{2}\) and \(Y = 2^{5} \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 13^{3}\) GCF(X, Y) = _______________________ |
|
b. If \(X = 3^{4} \cdots 5^{2} \cdots 7^{6}\) and \(Y = 2^{5} \cdots 3^{6} \cdots 5^{6} \cdots 7^{3}\) and \(Z = 2^{4} \cdots 3^{5} \cdots 5^{4}\) GCF(X, Y, Z) = _____________________ |
|
c. If \(X = a^{4} \cdots b^{2} \cdots c^{6} \cdots d^{3} \cdots e^{2}\) and \(Y = a^{5} \cdots c^{3} \cdots d^{4} \cdots e^{6} \cdots f^{3}\) GCF(X, Y) = _______________________ |
|
d. If \(X = a^{4} \cdots b \cdots c^{4} \cdots d^{3}\) and \(Y = a^{5} \cdots b^{3} \cdots d^{4} \cdots e^{6}\) and \(Z = a^{2} \cdots c^{3} \cdots d^{7} \cdots f^{3}\) GCF(X, Y, Z) = _____________________ |
If two numbers have no factors in common, they are called relatively prime. In other words, if GCF(a, b) = 1, then a and b are relatively prime. The numbers, a and b, might both be prime, both be composite, or one might be prime and the other composite.
Give an example of two composite numbers that are relatively prime:
Write a prime number and composite number that are relatively prime:
Assume GCF(28, x) = 1
a. List any prime numbers that are not factors of x: ________________________
b. Give three examples (numbers) of what x could equal: ___________________
If x and y are different prime numbers, GCF(x, y) = _____
If m is a whole number, find the following:
| a. GCF(2m, 3m) = _______ | b. GCF (4m, 10m) = ________ |
| c. GCF(m, m) = _______ | d. GCF( m, 1) = _______ |
| e. GCF(m, 0) = _______ |
Trying to find the greatest common factor of two large numbers by prime factorization is sometimes quite time-consuming. There are two other algorithms you can use that we'll use. One is called The Old Chinese Method, and the other is The Euclidean Algorithm. Both of these methods use a fact we can prove using what we know about divisibility. First, let's look at some examples.
Compute each of the following:
| a. List the common factors of 42 and 72: _______ |
| b. List the common factors of 42 and 30 (which is 72 – 42): _______ |
| c. List the common factors of 30 and 12 (which is 42 – 30): _______ |
| d. List the common factors of 12 and 18 (which is 30 – 12): _______ |
| e. List the common factors of 12 and 6 (which is 18 – 12): _______ |
| f. List the common factors of 6 and 6 (which is 12 – 6): _______ |
| g. List the common factors of 6 and 0 (which is 6 – 6): _______ |
Exercise 26
From your work in exercise 25, compute the following:
| a. GCF( 42, 72 ) = ____ | b. GCF( 42, 30 ) = ____ |
| c. GCF( 30, 12 ) = ____ | d. GCF( 12, 18 ) = ____ |
| e. GCF( 12, 6 ) = ____ | f. GCF( 6, 6 ) = ____ |
| g. GCF( 6, 0 ) = ____ |
The previous two exercises illustrate that the greatest common factor of two numbers is equal to the greatest common factor of the smaller number, and the difference of the original two numbers; i.e., if x \(\boldsymbol{\geq}\) y, then GCF(x, y) = GCF(y, x – y).
Prove the following theorem: Let a \(\boldsymbol{\geq}\) b. If c|a and c|b, then c|(a – b).
Solution: If c|a, then cn=a for some whole number, n. If c|b, then cm=b for some whole number, m. Using these substitutions for a and b, we get that c|(a – b) is true if c|(cn – cm) which is true if c is a factor of cn – cm. Factor: cn – cm = c(n – m). This clearly shows that c is indeed a factor of cn – cm. Therefore, if c|a and c|b, then c|(a – b).
This theorem can be used to show that if a \(\boldsymbol{\geq}\) b, then GCF(a, b) = GCF(b, a – b). The above theorem states that if c is a factor of two numbers, then it is also a factor of their difference. Hence, if c is a common factor of a and b, where a \(\geq\) b, then c is also a common factor of b and a – b. Since every common factor of a and b is also a common factor of ba and a – b, the pairs (a, b) and (b, a – b) have the same common factors. So, GCF(a, b) and GCF(b, a – b) must also be the same number.
The Old Chinese Method employs the fact that GCF(a, b) = GCF(b, a – b).
Note three more properties:
GCF(x, x) = x: GCF(x, x) states that the greatest common factor of the same two numbers is itself. That should be clear since x is the greatest factor of each number, so each has x as the greatest common factor.
GCF(x, 0) = x: GCF(x, 0) = x, is true since every number is a factor of zero. So, since x is the greatest factor of x, then x is the greatest common factor of x and 0.
GCF(x, 1) = 1: GCF(x, 1) = 1 is true since 1 is a factor of every number, including x, and 1 is the only factor of 1. Therefore, 1 must be the greatest common factor of 1 and x.
Old Chinese Method of finding the greatest common factor of two numbers:
Write the GCF of the two numbers in parentheses (remember the order of the numbers is irrelevant). Let that equal the GCF of the smaller of the two numbers, and the difference of the original two numbers. If the numbers in the parentheses are the same, that number is the GCF; if one the new numbers is 1, 1 is the GCF. Otherwise, repeat the process until the two numbers are the same, or 1 is one of the numbers. An example is shown below. On the right is an explanation of how I obtained the two new numbers in parentheses. The new numbers are underlined in the explanation. You do not need to write that out.
| GCF(546, 390) | = GCF(390, 156) | (390 is smaller than 546, 156 = 546 – 390) |
| = GCF(156, 234) | (156 is smaller than 390, 234 = 390 – 156) | |
| = GCF(156, 78) | (156 is smaller than 234, 78 = 234 – 156) | |
| = GCF(78, 78) | (78 is smaller than 156, 78 = 156 – 78) | |
| = 78 | 78 is the GCF(78, 78); The answer is a number! |
Therefore, GCF(546, 390) = 78.
Check: First, make sure 78 is a factor of 546 and 390: \(546 = 78 \cdots 7\) and \(390 = 78 \cdots 5\). Second, check to make sure the other factors of each (7 and 5) are relatively prime. If so, then 78 is not only a factor of 546 and 390, but is in fact the greatest common factor of each since they have no other common factors (because 7 and 5 have no common factors).
Another example is shown below. On the right is an explanation of how I obtained the two new numbers (underlined) in parentheses. You do not need to write that out.
| GCF(1200, 504) | = GCF(504, 696) | (504 is smaller than 1200, 696 = 1200 – 504) |
| = GCF(504, 192) | (504 is smaller than 696, 192 = 696 – 504) | |
| = GCF(192, 312) | (192 is smaller than 504, 312 = 504 – 192) | |
| = GCF(192, 120) | (192 is smaller than 312, 120 = 312 – 192) | |
| = GCF(120, 72) | (120 is smaller than 192, 72 = 192 – 120) | |
| = GCF(72, 48) | (72 is smaller than 120, 48 = 120 – 72) | |
| = GCF(48, 24) | (48 is smaller than 72, 24 = 72 – 48) | |
| = GCF(24, 24) | (24 is smaller than 48, 24 = 48 – 24) | |
| = 24 | 24 is the GCF(24, 24); The answer is a number! |
Therefore, GCF(1200, 504) = 24.
Check: First, make sure 24 is a factor of 1200 and 504: 1200 = \(24 \cdots 50\) and \(502 = 24 \cdots 21\). Second, check to make sure the other factors of each (25 and 21) are relatively prime. If so, then 24 is not only a factor of 1200 and 504, but is in fact the greatest common factor of each since they have no other common factors (because 25 and 21 have no common factors.)
Here is one more example:
| GCF(667, 437) | = GCF(437, 230) | |
| = GCF(230, 207) | ||
| = GCF(207, 23) | ||
| = GCF(23, 184) | ||
| = GCF(23, 161) | ||
| = GCF(23, 138) | ||
| = GCF(23, 115) | ||
| = GCF(23, 92) | ||
| = GCF(23, 69) | ||
| = GCF(23, 46) | ||
| = GCF(23, 23) | ||
| = 23 | Remember: The answer is a number! |
Therefore, GCF(667, 437) = 23.
Check: First, make sure 23 is a factor of 667 and 437: \(667 = 23 \cdots 29\) and \(437 = 23 \cdots 19\). Second, check to make sure the other factors of each (29 and 19) are relatively prime. If so, then 23 is not only a factor of 667 and 437, but is in fact the greatest common factor of each since they have no other common factors (because 29 and 19 have no common factors.)
A comment: You could have obtained the greatest common factor of the previous three examples by prime factoring. Often, this is a lengthy process for large numbers that look like they might be prime, as in the last example. Therefore, the Old Chinese provides an alternative way to obtain the greatest common factor. After doing a few using this method, we'll explore another alternate method, called the Euclidean Algorithm, which is related to, but usually takes less steps than, the Old Chinese Method.
Use the Old Chinese Method to compute the greatest common factor of the numbers given. Use correct notation, and show each step. State the answer. Then, show how you check your answer. Use the previous example as a model to do these problems.
|
a.
|
||||||||||||||||||||||||||||||
|
b.
|
||||||||||||||||||||||||||||||
|
c.
|
Using the Chinese Method could be quite tedious. Take a look at the following example:
| GCF(1200, 504) | = GCF(504, 696) | (504 is smaller than 1200, 696 = 1200 – 504) |
| = GCF(504, 192) | (504 is smaller than 696, 192 = 696 – 504) | |
| = GCF(192, 312) | (192 is smaller than 504, 312 = 504 – 192) | |
| = GCF(192, 120) | (192 is smaller than 312, 120 = 312 – 192) | |
| = GCF(120, 72) | (120 is smaller than 192, 72 = 192 – 120) | |
| = GCF(72, 48) | (72 is smaller than 120, 48 = 120 – 72) | |
| = GCF(48, 24) | (48 is smaller than 72, 24 = 72 – 48) | |
| = GCF(24, 24) | (24 is smaller than 48, 24 = 48 – 24) | |
| = 24 | 24 is the GCF(24, 24); The answer is a number! |
In the beginning of this example, GCF(1200, 504), we had to subtract 504 twice until we got GCF(504, 192). Then, notice once we wrote GCF(504, 192), we had to subtract 192 twice until we got GCF(192, 120). Basically, we do repeated subtraction until we get a number smaller than the one we are subtracting. Repeated subtraction is actually division. Note that \(1200 \div 504 = 2\) remainder 192. On the second step, we see GCF(504, 192), which has the smaller of the numbers in the original parentheses (504), and the remainder after dividing the larger number (1200) by the smaller number (504). Note that \(504 \div 192 = 2\) remainder 120. Look at the fourth step: we see GCF(192, 120), which has the smaller of the numbers in GCF(504, 192), and the remainder after dividing the larger number (504) by the smaller number (192). The Euclidean Algorithm uses division instead of repeated subtraction to shorten the steps.
How to use the Euclidean Algorithm to find the greatest common factor of two numbers:
Write the GCF of the two numbers in parentheses (remember the order of the numbers is irrelevant). The smaller of the two numbers will be one of the numbers in the next parentheses. To get the other number, divide the larger number by the smaller number, and put the remainder in parentheses. If the the smaller number is a factor of the larger number, that means it will divide evenly, so there will be no remainder. That means the remainder is 0. Remember to put the remainder in the parentheses, not the quotient! If one of the new numbers in the parentheses is zero, the other number is the GCF; if one the new numbers is 1, 1 is the GCF. Otherwise, repeat the process until one of the two numbers is 0 or 1. An example is shown below. This is the first example we did using the Old Chinese Method. You might want to look back and compare. On the right is an explanation of how I obtained the two new numbers in parentheses.
| GCF(546, 390) | = GCF(390, 156) | (390 is smaller than 546, \(546 \div 390\) = 1 r 156) |
| = GCF(156, 78) | (156 is smaller than 390, \(390 \div 156\) = 2 r 78) | |
| = GCF(78, 0) | (78 is smaller than 156, \(156 \div 78\) = 2 r 0) | |
| = 78 | Put the remainder (0), NOT 2, in the parentheses! | |
| 78 is the GCF(78, 78); The answer is a number! |
Therefore, GCF(546, 390) = 78
Check: First, make sure 78 is a factor of 546 and 390: \(546 = 78 \= \cdots 7\) and \(390 = 78 \cdots 5\). Second, check to make sure the other factors of each (7 and 5) are relatively prime. If so, then 78 is not only a factor of 546 and 390, but is in fact the greatest common factor of each since they have no other common factors (because 7 and 5 have no common factors
Below is another example – we did this earlier using the Old Chinese Method. On the right is an explanation of how I obtained the two new numbers in parentheses. You do not need to write that out.
| GCF(667, 437) | = GCF(437, 230) | (437 is smaller than 667, \(667 \div 437 = 1\) r 230) |
| = GCF(230, 207) | (230 is smaller than 437, \(437 \div 230 = 1\) r 207) | |
| = GCF(207, 23) | (207 is smaller than 230, \(230 \div 207\) = 1 r 23) | |
| = GCF(23, 0) | (23 is smaller than 207, \(207 \div 23\) = 9 r 0) | |
| = 23 | Put the remainder (0), NOT 9, in the parentheses! | |
| Remember: The answer is a number! |
Therefore, GCF(667, 437) = 23
Check: First, make sure 23 is a factor of 667 and 437: 667 = \(23 \cdots 29\) and \(437 = 23 \cdots 19\). Second, check to make sure the other factors of each (29 and 19) are relatively prime. If so, then 23 is not only a factor of 667 and 437, but is in fact the greatest common factor of each since they have no other common factors (because 29 and 19 have no common factors.)
A comment: You could have obtained the greatest common factor of the previous three examples by prime factoring, the Old Chinese Method or the Euclidean Algorithm.
CAUTION: THE MOST COMMON MISTAKE PEOPLE MAKE WHEN USING THE EUCLIDEAN ALGORITHM IS ON THE LAST STEP, WHEN THE SMALLER NUMBER DIVIDES EVENLY INTO THE LARGER NUMBER, WHICH MEANS THE REMAINDER IS ZERO. IT DOESN'T MATTER WHAT THE QUOTIENT IS – IT'S THE REMAINDER THAT MATTERS – 0 GOES IN THE PARENTHESES!!! Also, zero is not a factor of any number except zero, so the GCF can't be zero. On the other hand, every number is a factor of zero. So, when zero is one of the numbers in parentheses, the other number is the GCF. REMEMBER TO ALWAYS CHECK YOUR Answer!!!
Before going on, I'm going to remind you of a quick and easy way to find out the quotient and remainder by using a simple calculator when doing these division problems, where you need to find the remainder. If you can already do it easily or your calculator figures it out for you, skip on down to Exercise 29. Let's say you wanted to divide \(5263 \div 360\). When you do this on your calculator, it shows up something like 14.619444. This indicates that there are 14 360's in 5263, but the remainder isn't evident. At least, you know 14 is the quotient. To find the remainder on your calculator, key in \(14 \times 360\) - 5263 and the number showing is the remainder if you ignore the negative sign! In this case, the remainder is 223. Remember that the remainder must be less than what you originally divided by – less than 360 in this case. Think about why this process works and try it on the next few problems.
Use a calculator to find the quotient and remainder for these division problems.
| a. \(9876 \div 255\) = | b. \(1509 \div 164\) = |
| c. \(333 \div 46\) = | d. \(4657 \div 579\) = |
Use the Euclidean Algorithm to compute the greatest common factor of the numbers given. Use correct notation, and show each step. State the answer. Then, show how you check your answer. Use the previous example as a model to do these problems. These are the same exercises you did using the Old Chinese Method in exercise 27. You might want to compare the two methods when you are done. Of course, the answer should be the same.
|
a.
|
|||||||||||||||
|
b.
|
|||||||||||||||
|
c.
|
Find GCF(418, 88) using the three methods discussed:
| a) by prime factorization; |
| b) by the Old Chinese Method; |
| c) by the Euclidean Algorithm |
| d) Write the answer, and show how to check the answer. |
| a. Use prime factorization | c. Use the Euclidean Algorithm |
| b. Use the Old Chinese Method | d. Answer: GCF(418, 88) = _______ Check your answer |
Find GCF(527, 465) using the three methods discussed:
| a) by prime factorization; |
| b) by the Old Chinese Method; |
| c) by the Euclidean Algorithm |
| d) Write the answer, and show how to check the answer. |
| a. Use prime factorization | c. Use the Euclidean Algorithm |
| b. Use the Old Chinese Method | d. Answer: GCF(527, 465) = _______ Check your answer |
Find GCF(353, 213) using the three methods discussed:
| a) by prime factorization; |
| b) by the Old Chinese Method; |
| c) by the Euclidean Algorithm |
| d) Write the answer, and show how to check the answer. |
| a. Use prime factorization | c. Use the Euclidean Algorithm |
| b. Use the Old Chinese Method | d. Answer: GCF(353, 213) = _______ Check your answer |
Now that we've covered a lot about prime numbers and factoring, we are going to revisit the divisibility tests one more time.
Note that the divisibility test for 6 utilized two other divisibility tests, the one for 2 and the one for 3. Also, note that the divisibility test for 15 utilized two other divisibility tests, the one for 5 and 3. Why do you think that works? What is the procedure for figuring out what tests to use?
Fact: If each prime in the prime factorization of a composite number, c, is listed only once, the divisibility test for that composite number is this: c|n if each of the prime factors of c divide n.
The prime factorization for 6 is \(2 \cdot 3\). Since both primes are only listed once, the divisibility test for 6 is the union of the divisibility tests for 2 and 3.
The prime factorization for 15 is \(5 \cdot 3\). Since both primes are only listed once, the divisibility test for 15 is the union of the divisibility tests for 5 and 3.
Write the divisibility test for 14:
Use the divisibility test for 14 to see which of the following is true. Show work.
| a. 14|742 |
| b. 14|968 |
| c. 14|483 |
The prime factorization for 20 is \(2 \cdots 2 \cdots 5\). The divisibility test for 2, 2 and 5 does not work since 20|70 is false even though 2|70 and 2|70 and 5|70. Why doesn't it work?
This is the divisibility test for 20: 20|n if 4|n and 5|n. Why do you think this works?
Try to write the divisibility tests for each of the following numbers:
| a. 12|n if |
| b. 18|n if |
Divisibility Test for a composite number: Assume \(P_{1}, P_{2}, P_{3}, P_{4}, P_{5}\),... are all different prime numbers. (You can think of \(P_{1}\) as the first prime (2), \(P_{2}\) as the second prime (3), \(P_{3}\) as the third prime (5), \(P_{4}\) as the fourth prime (7), \(P_{5}\) as the fifth prime (11), etc. Assume the prime factorization of a number, c, is \((P_{a})^{x} \cdots (P_{b})^{y} \cdots ... \cdots (P_{c})^{z}\) where \(P_{a} \neq P_{b} \neq P_{c}\), etc. Then, c|n if \((P_{a})^{x}\)|n AND \((P_{b})^{y}\)|n AND \((P_{c})^{z}\)|n, etc.
The divisibility test for the following numbers is done by first factoring them.
1) Divisibility test for 26: Since 26 = \(2 \cdots 13\): 26|n if 2|n and 13|n.
2) Divisibility test for 12: Since 12 = \(2^{2} \cdots 3\): 12|n if 4|n and 3|n.
3) Divisibility test for 24: Since 24 = \(2^{3} \cdots 3\): 24|n if 8|n and 3|n.
4) Divisibility test for 45: Since 45 = \(3^{2} \cdots 5\): 45|n if 9|n and 5|n.
5) Divisibility test for a number, c, whose prime factorization is \(2^{3} \cdots 3^{2} \cdots 5^{2} \cdots 11\): c|n if 8|n AND 9|n and 25|n and 11|n
7) Divisibility test for a number, b, whose prime factorization is \(3^{2} \cdots 5 \cdots 7^{2} \cdots 11^{2}\): b|n if 9|n AND 5|n and 49|n and 121|n
Write the divisibility test for the following numbers:
| a. 35: ____ |
| b. 28: ____ |
| c. 75: ____ |
| d. 56: ____ |
| e. A number, c, whose prime factorization is \(2^{2} \cdots 3^{3} \cdots 5^{2} \cdots 11\): ____ |
| f. A number, d, whose prime factorization is \(2^{4} \cdots 3 \cdots 5 \cdots 11\): ____ |
This exercise is for you to think about what you'd do if someone asked you to find the LEAST common factor of a set of numbers, instead of the greatest common factor.
| a. Find the least common factor of 55 and 66: ____ |
| b. Find the least common factor of 10 and 12: ____ |
| c. Find the least common factor of 1 and 8: ____ |
| d. Find the least common factor of 3, 6, and 9: ____ |
| e. Find the least common factor of m and n: ____ |
| f. Do you think it is a useful question to find the least common factor of a set of numbers? Why or why not? Explain your answer. |
| g. What is the least common factor of any set of numbers? ____ |


