8.3: LCM and other Topics

You will need: Prime Number Squares (Material Cards 19A-19B)

Composite Number Squares (Material Cards 20A-20B)

There are a finite number of factors for any given number. On the other hand, there are an infinite number of nonzero multiples of a number. For instance the list of multiples of 2 are all of the even numbers. It's impossible to list all of them, because this is an infinite set. A multiple of a number c is nc where n is a whole number. In other words, to find a multiple of c, multiply c by a whole number. Although 0 is a multiple of every number, we usually omit listing it as a multiple. The (nonzero) multiples of 6 are listed here: 6, 12, 18, 24, 30, 36, 42, ...

To list the multiples of a number, you begin with the number itself, then the number times 2, then the number times 3, etc. Since multiplication is repeated addition, you could repeatedly add the number to get the next multiple.

Exercise 1

a. List the first 10 multiples of 8:

b. List the first 10 multiples of 12:

c. Of the list you produced in parts a and b, list the multiples that 8 and 12 have in common:

d. From part c, what is the smallest multiple that 8 and 12 have in common?

e. Is there a greatest common multiple that 8 and 12 have in common? Is so, what is it? Before you answer, remember that in a and b, you only listed the first 10 multiples of 8 and 12.

Just like with the greatest common factor (GCF), many people don't really think about what LEAST COMMON MULTIPLE means. Every number has an infinite number of multiples. Every set of numbers has an infinite number of multiples in common. The LEAST COMMON MULTIPLE is the smallest multiple they have in common.

In exercise 1, we write LCM(8, 12) = 24. The order of the numbers in the parentheses is irrelevant. So, LCM(8, 12) = LCM(12, 8). It is NOT an ordered pair. Also, you can find the least common multiple of a large set of numbers. Soon, you'll find how easy it is to find the least common multiple of several numbers; e.g., LCM(2, 3, 4, 5, 6, 7, 8, 9, 10). In this case, listing several multiples of each of these numbers until you find the smallest one all of them have in common is not the efficient way to find it, so you'll be exploring another way to find it using prime factorization.

Exercise 2

a. List the first 15 multiples of 4:

b. List the first 15 multiples of 6:

c. List the first 15 multiples of 10:

d. Of the list you produced in parts a, b and c, list the multiples all three numbers (4, 6 and 10) have in common:

e. From part d, complete the following: LCM(4, 6, 10) =

The problem with trying to find the least common multiple this way is that you may have to write a lengthy list of multiples of each number until you finally find a multiple they all have in common. For instance, if you were asked to find the LCM(59,61), you wouldn't find a multiple they each have in common until you wrote 61 multiples of 59 and 59 multiples of 61. That is because these are prime numbers, so the least common multiple is their product: \(59 \cdots 61\). This is the case with any numbers that are relatively prime as well. (Remember 4 and 15 are relatively prime, although neither is prime.)

If x and y have no factors in common, then GCF(x,y) = 1 and LCM(x,y) = xy.

The following is also true:

If GCF(x,y) = 1, then x and y have no factors in common, and LCM(x,y) = xy.

If LCM(x,y) = xy, then x and y have no factors in common, and GCF(x,y) = 1.

A more efficient way to find the least common multiple of a set of numbers is to find the prime factorization of each number, and then BUILD the least common multiple. Get out your prime number squares to do the following exercises.

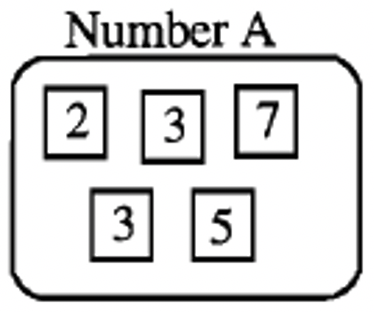
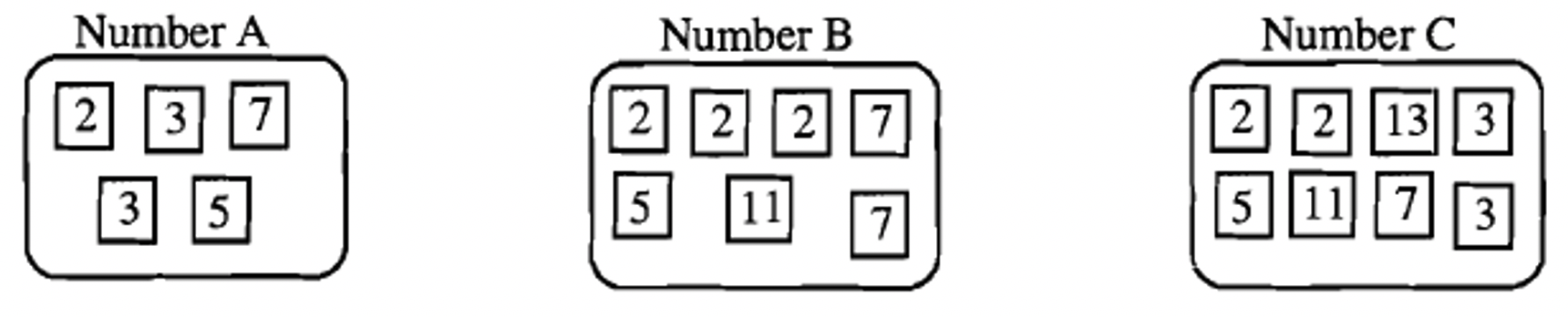
Below is the prime factorization of three numbers, A, B and C.

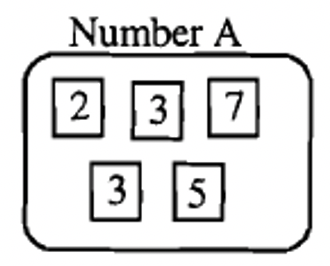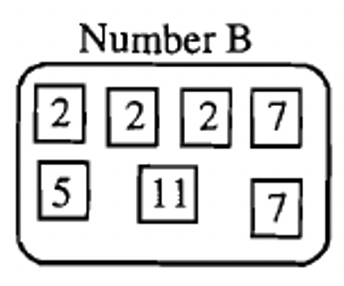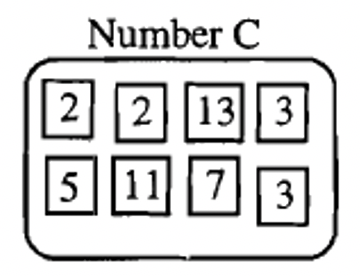Below is how to write each of these numbers in prime factorization form:

\(A = 2 \cdots 3^{2} \cdots 5 \cdots 7\)

\(B = 2^{3} \cdots 5 \cdots 7^{2} \cdots 11\)

\(C = 2^{2} \cdots 3^{2} \cdots 5 \cdots 7 \cdots 11 \cdots 13\)

One way to make a multiple of A is to simply add extra factors to factors of A. Note: A itself is a multiple of A, so you don't have to add any extra factors to get a multiple. There are an infinite number of possibilities for multiples of A. Below are three multiples of A:

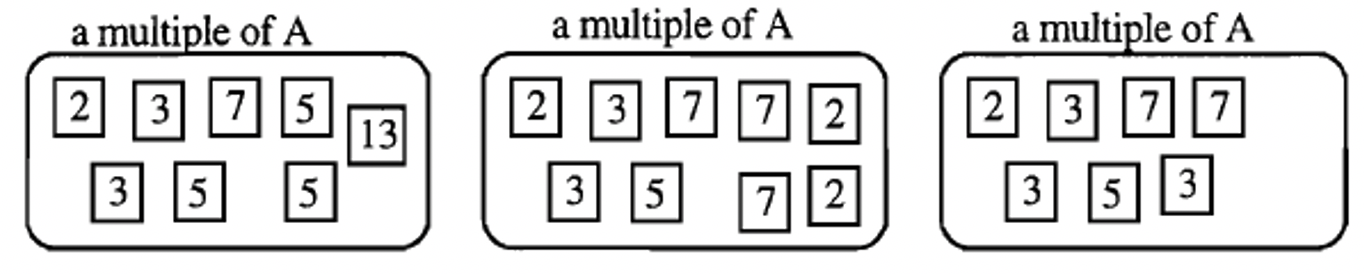
In prime factorization form, the first multiple of A above is written: \(2 \cdots 3^{2} \cdots 5^{3} \cdots 7 \cdots 13\)

Exercise 3

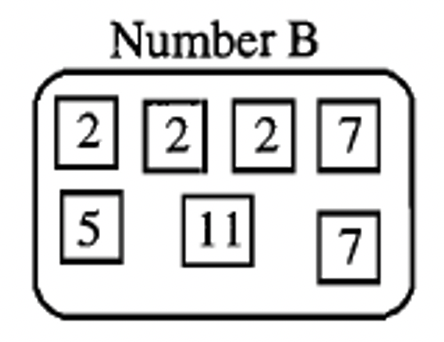
Below is the prime factorization of a number, B

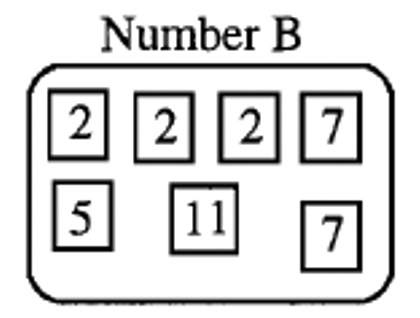
a. Form the number B with your prime number squares. Form a multiple of B by "throwing in" one or more prime number squares as factors to the original prime factorization of B shown above. Show a picture of the multiple of B that you formed.

Write the prime factorization of this multiple: _____

b. Form the number B with your prime number squares. Form a multiple of B, different from the one you formed in A, by "throwing in" one or more prime number squares as factors to the original prime factorization of B shown above. Show a picture of the multiple of B that you formed:

Write the prime factorization of this multiple of B: _____

c. Form the number B with your prime number squares. Form another multiple of B by "throwing in" one or more prime number squares as factors to the original prime factorization of B shown above. Write the prime factorization of this multiple of B: _____

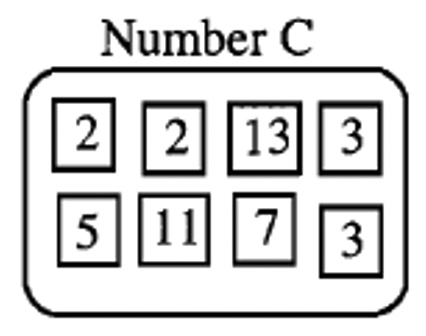
Number C is shown below toward the middle of the page. Use it to do exercise 4.

Exercise 4

a. Form the number C with your prime number squares. Form a multiple of C by adding one or more prime number squares as factors. Write the prime factorization of the multiple of C you formed:

b. Form the number C with your prime number squares. Form a different multiple of C by adding one or more prime number squares as factors. Write the prime factorization of the multiple of C you formed:

c. Form the number C with your prime number squares. Form another multiple of C by adding one or more prime number squares as factors. Write the prime factorization of the multiple of C you formed:

NOTE: X is a multiple of M if M is a factor of X. So, you have a multiple of a number if the prime factors of the number itself are factors in the multiple. It's as if you can "see" the number in a multiple. We are going to determine if any of the numbers shown on the right are multiples of A, B or C.

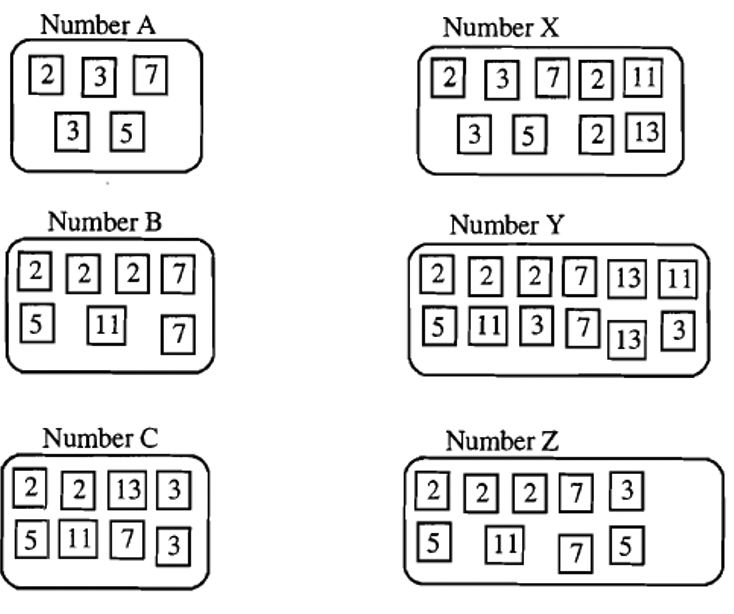
To decide if X, Y or Z is a multiple of A, see if each of X, Y or Z has the prime factors of A as a subset. In other words, A has one factor of 2, two factors of 3, one factor of 5 and one factor of 7. Any number containing those factors is a multiple of A. A multiple of A may have more factors of A, but can't be missing any factors of A.

Exercise 5

a. List any number on the right (X, Y and/or Z) that is a multiple of A:

b. List any number on the right (X, Y and/or Z) that is a multiple of B:

c. List any number on the right (X, Y and/or Z) that is a multiple of C:

None of the numbers X, Y or Z was a multiple of all three of the numbers, A, B and C. Numbers A, B and C are shown below. Below that are only two examples of multiples that A, B and C have in common.

Exercise 6

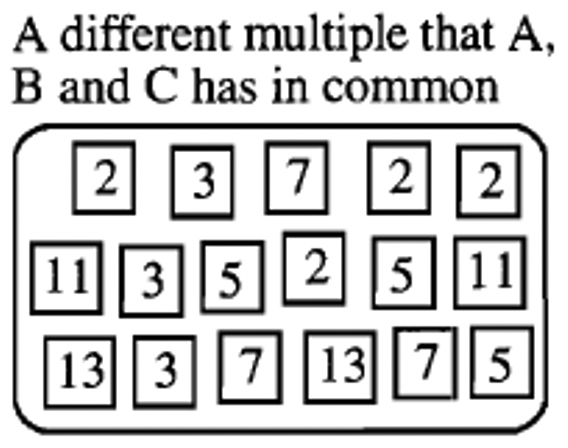Use prime number squares to form three other multiples that A, B and C have in common. Write the prime factorization of each of the multiples you formed.

a. _____

b. _____

c. _____

Now, we are going to use the prime factorization to build the LEAST COMMON MULTIPLE of a set of numbers. The least common multiple is a multiple that the numbers have in common, but that has the least number of factors possible. The multiples formed above have 16 and 17 factors, respectively. To build a least common multiple, we only add in a factor if it is necessary.

Let's say we want to build the least common multiple of A, B and C. In order to be a multiple of A, we need to have the factors of A. So, we start building the multiple by putting in the factors of A:

The factors of B must also be in the multiple. B has three factors of 2, but there is only one factor of 2 in the multiple so far. So, the common multiple will need two more factors of 2. B has two factors of 7, but there is only one factor of 7 in the multiple so far. So, the common multiple will need one more factor of 7. B has one factor of 5, which is already there. B also has one factor of 11. That is not there, so must be put in. Therefore, two factors of 2, one factor of 7 and a factor of 11 must be joined with the other factors in the common multiple. Once this is done, we have built the least common multiple of A and B:

The prime factorizations of A, B and C are shown below for your convenience.

We have built the least common multiple of A and B. To find the least common multiple of A, B and C, we need to make sure the factors of C are also in the multiple. C has two factors of 2, which are already in the multiple, two factors of 3, which are already in the multiple, one factor each of 5, 7 and 11, each of which is already in the multiple, and a factor of 13, which is not in the multiple. So 13 is the only factor that needs to be joined with the factors already in the multiple we are building.

The above is a multiple of A, B and C. We only have we built a multiple, we actually built the LEAST COMMON MULTIPLE of A, B and C. Note it is a multiple of A, B and C; therefore it is a common multiple. It is the least common multiple because if any of the factors were removed, it wouldn't be a multiple of one of the numbers. For instance, if a factor of 2 was removed, it would not be a multiple of A. If a factor of 3 was removed, it would not be a multiple of A or C. If a factor of 7 was removed, it would not be a multiple of B, etc. If a factor of 11 was removed, it would not be a multiple of B or C. If a factor of 13 was removed, it would not be a multiple of C.

We write: LCM(A, B, C) = \(2^{3} \cdots 3^{2} \cdots 5 \cdots 7^{2} \cdots 11 \cdots 13\)

Exercise 7

Build the least common multiple of A and B using prime number squares. Then, write the prime factorization of the least common multiple of A and B. Let \(A = 2^{2} \cdots 3^{5} \cdots 5 \cdots 13\) and \(B = 2^{2} \cdots 3^{2} \cdots 7^{3} \cdots 11^{2} \cdots 13\)

LCM(A, B) = ____

Exercise 8

Build the least common multiple of A, B and C using prime number squares. Then, write the prime factorization of the least common multiple of A and B.

Let A = \(2^{2} \cdots 11 \cdots 19\) and \(B = 2 \cdots 3^{2} \cdots 7 \cdots 11^{2}\) and \(C = 2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 13^{2} \cdots 19\)

LCM(A, B, C) = _____

Exercise 9

Build the least common multiple of A, B and C using prime number squares. Then, write the prime factorization of the least common multiple of A and B.

Let \(A = 2 \cdots 5^{3} \cdots 11 \cdots 19\) and \(B = 2^{4} \cdots 3^{6} \cdots 5^{2} \cdots 23^{2}\) and \(C = 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 23\)

LCM(A, B, C) = _____

Look back at the answer from exercise 9.

Let \(A = 2 \cdots 5^{3} \cdots 11 \cdots 19\) and \(B = 2 \cdots 3^{6} \cdots 5^{2} \cdots 23^{2}\) and \(C = 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 23\)

Answer: LCM(A, B, C) = \(2 \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 19 \cdots 23^{2}\)

If the numbers are prime factored using exponents, then the least common multiple contains each of the prime factors shown in any of the numbers. The exponent on each of the prime numbers is the highest exponent found on that prime number factor in the prime factorization of the numbers.

For instance, the prime numbers in the prime factorization of A, B and C are 2, 3, 5, 7, 11, 19 and 23. So begin by writing the product of these prime numbers: \(2 \cdots 3 \cdots 5 \cdots 7 \cdots 11 \cdots 19 \cdots 23\)

2 is a factor in A and B. The highest power of 2 found in either prime factorization of A and B is 1. 3 is a factor found in B, as \(3^{6}\). So, the highest power of 3 is 6. 5 is a factor of all three numbers. In A, the exponent on 5 is 3; in B, the exponent on 5 is 2; in C, the exponent on 5 is 4. So, the highest power of 5 is 4. Similarly, do the same for all of the other prime factors. Write the highest exponent on the factor.

Therefore, LCM(A, B, C) = \(2 \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 19 \cdots 23^{2}\)

Exercise 10

Find the greatest common factor and least common multiple for each set of numbers, written in prime factorization. Assume a, b, c, d, and e are different prime numbers.

a. Let \(A = 2^{2} \cdots 3^{5} \cdots 5 \cdots 13\) and \(B = 2^{2} \cdots 3^{2} \cdots 7^{3} \cdots 11^{2} \cdots 13\)

GCF(A, B) = ____________________________________________________

LCM(A, B) = ____________________________________________________

b. Let \(A = 2^{2} \cdots 11 \cdots 19\) and \(B = 2 \cdots 3^{2} \cdots 7 \cdots 11^{2}\) and \(C = 2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 13^{2} \cdots 19\)

GCF(A, B, C) = __________________________________________________

LCM(A, B, C) = __________________________________________________

c. Let \(X = a^{5} \cdots b^{4} \cdots c^{5} \cdots d\) and \(Y = b^{2} \cdots c^{3} \cdots d^{2} \cdots e^{2}\) and \(Z = a^{2} \cdots c^{4} \cdots d^{3} \cdots e^{2}\)

GCF(X, Y, Z) = __________________________________________________

LCM(X, Y, Z) = __________________________________________________

d. Let \(X = a^{6} \cdots b^{3} \cdots c \cdots d\) and \(Y = b^{4} \cdots c^{4} \cdots d^{3} \cdots e^{7}\) and \(Z = a^{2} \cdots c^{4} \cdots d^{2} \cdots e^{3}\)

GCF(X, Y, Z) = __________________________________________________

LCM(X, Y, Z) = __________________________________________________

So far, the prime factorization of numbers has been given, and all you had to do was to build the prime factorization of the least common multiple. Now, your job will be to first prime factor numbers; then you can build the least common multiple from the prime factorizations. In the end, the least common multiple is a number. Multiply the factors in the least common multiple to find the one number that is the least common multiple.

Example

Find the least common multiple of 15, 18 and 20

Solution

Prime factor each of these numbers. \(15 = 3 \cdots 5, 18 = 2 \cdots 3 \cdots 3\), and \(20 = 2 \cdots 2 \cdots 5\)

Build the least common multiple by first "throwing in" the prime factors that make up the prime factorization of 15; then "throw in" any prime factors needed for 18; next, "throw in" any prime factors needed for 20. We get

LCM(15, 18, 20) = \(3 \cdots 5 \cdots 2 \cdots 3 \cdots 2 = 2^{2} \cdots 3^{2} \cdots 5\) = 180

Exercise 11

Find the least common multiples. Show the prime factorization of each number, and how you use it to build the least common multiple.

a. LCM (6, 8, 10) = ______

b. LCM (25, 35, 40) = ______

c. LCM (49, 91, 26) = ______

d. LCM(56, 24, 30) = ______

e. LCM(22, 34, 55) = _____

Note how easy it is to find the least common multiple of a larger set of numbers using prime factorization. We'll find: LCM(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14)

We don't need to expressly write down the prime factorization of the 12 numbers because it's easy enough to do that in our head. For instance, the prime factorization of 4 is \(2 \cdots 2\), the prime factorization of 10 is \(2 \cdots 5\), and the prime factorization of 13 is 13.

We build up the LCM of 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 by first making sure the prime factorization of 2 is there.

Step 1: Make sure the prime factorization 2 is there. So far, LCM: 2

Step 2: Make sure the prime factorization 3 is there. We need to "throw in" a 3 to the LCM. So far, LCM: \(\bf 2 \cdots 3\)

Step 3: Make sure the prime factorization 4 is there. We need to "throw in" a 2 to the LCM. So far, LCM: \(\bf2 \cdots 3 \cdots 2\)

Step 4: Make sure the prime factorization 5 is there. We need to "throw in" a 5 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5\)

Step 5: Make sure the prime factorization 6 is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: \(2 \cdots 3 \cdots 2 \cdots 5\).

Step 6: Make sure the prime factorization 7 is there. We need to "throw in" a 7 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7\)

Step 7: Make sure the prime factorization 8 is there. We need to "throw in" a 2 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2\)

Step 8: Make sure the prime factorization 9 is there. We need to "throw in" a 3 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3\)

Step 9: Make sure the prime factorization 10 is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3\)

Step 10: Make sure the prime factorization 11 is there. We need to "throw in" an 11 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11\)

Step 11: Make sure the prime factorization 12 is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11\)

Step 12: Make sure the prime factorization 13 is there. We need to "throw in" a 13 to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\)

Step 13: Make sure the prime factorization 14 is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: \(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\)

That's it! You have now built up the LEAST common multiple of all 12 numbers! You can check to make sure that the prime factorization of each of the 12 numbers is indeed in the prime factorization of the least common multiple you built. Furthermore, if any of the prime factors were removed, it wouldn't be a multiple of all 12 numbers. Therefore, the prime factorization of the LCM is as shown below:

LCM(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) = \(2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\).

If these factors are multiplied together, LCM(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) = 360, 360.

The prime factorization of the LCM may have been written with the factors in ascending order using exponents: \(2^{3} \cdots 3^{2} \cdots 5 \cdots 7 \cdots 11 \cdots 13\)

Exercise 12

Use prime factorization to build the least common multiple. Show the prime factorization as the number is built. Then, multiply the factors to find the answer.

a. LCM(3, 4, 6, 7, 9, 10, 12, 14, 15, 18, 20) = _______ = _______

b. LCM(2, 3, 9, 11, 14, 15, 16, 17, 18, 22) = _______ = ________

c. LCM(5, 6, 7, 8, 12, 14, 15, 17, 18, 25) = _______ = _______

d. LCM(15, 18, 20, 25, 30, 35, 42, 45) = _______ = _______

Let's say you know the greatest common factor of 165 and some other number was 3, and the least common multiple of the same two numbers was 15,015. How would you figure out what the other number was?

First, it's a good idea to write down what you know. Let N be the other number.

Then, GCF(165, N) = 3 and LCM (165, N) = 15,015.

Since 3 is a factor, and in fact the greatest common factor, of both 165 and N, then each number can be written as 3 times something, and the other factor you obtain for 165 should be relatively prime to the other factor you obtain for N, since 3 is the greatest common factor of 165 and N.

So, let’s rewrite, LCM (165,N) = 15,015 like this: LCM (\(3 \times 55\), \(3 \times\) _____ ) = 15,015

In other words, I know N = 3 \(\times\) _____, but I have to figure out what goes in the blank to figure out what N is. If you want to introduce another variable, like M, instead of writing a blank, that works just as well. It's up to you.

To find the LCM of \(3 \times 55\) and 3 \(\times\) ______ , where the 55 and the number on the blank have no common factors, you would multiply \(3 \times 55 \times\) _______. But we know the product should be 15,015. So, the number that must go on the blank must be 91, since \(3 \times 55 \times 91 = 15,015\). So, now we can figure out what N is: \(N = 3 \times 91 = 273\).

Let's see if this makes sense by first rewriting 165 and 273 either in prime factored form or as the GCF(165,273) times something; then we'll figure out the GCF and LCM from the factored form, and see if it agrees with our original problem.

\(165 = 3 \times 55\) and 273 = \(3 \times 91\). First, make sure 3 is really a factor of each number!

Now, convince yourself that 3 really is the greatest common factor of 165 and 273 by checking to see that the other factor of one number is relatively prime (no factors in common) with the other factor of the other number. So, ask yourself if 55 and 91 have any factors in common (besides 1) if you aren't sure, then prime factor each of these numbers first (\(55 = 5 \times 11\) and \(91 = 7 \times 13\)); note that they have no factors in common.

Since 3 is the greatest common factor, then the least common multiple is obtained by multiplying \(3 \times 55 \times 91\), which is 15,015 which is what it should be according to the original information given. Therefore, 273 really was the number we were looking for.

N = 273

There is another way to do the above problem using the following property:

For any two numbers, m and n, the following is always true:

\(m \times n = GCF(m, n) \times LCM (m, n)\)

This equation is not true for more than two numbers \(r \times s \times t \neq GCF(r, s, t) \times LCM(r, s, t)\)

Example

Verify the above property for numbers 15 and 18.

Since GCF(15, 18) = 3 and LCM(15, 18) = 90, we want to verify that the product of the two numbers, 15 and 18, equals the product of the GCF and LCM of the two numbers.

\(15 \cdots 18 = 270\); GCF(15, 18) \(\cdots\) LCM(15, 18) = \(3 \cdots 90 = 270\)

Therefore, \(15 \cdots 18 =\) GCF(15, 18) \(\cdots\) LCM(15, 18)

Example

Show that the above property does not work for three numbers.

Counterexample: Use the numbers 4, 6 and 8. GCF(4, 6, 8) = 2 and LCM(4, 6, 8) = 24

\(4 \cdots 6 \cdots 8 = 192\); GCF(4, 6, 8) \(\cdots\) LCM(4, 6, 8) = \(2 \cdots 24 = 48\)

Clearly, \(4 \cdots 6 \cdots 8 \neq\) GCF(4, 6, 8) \(\cdots\) LCM(4, 6, 8)

Example

Find N if GCF(165, N) = 3 and LCM (165, N) = 15,015

In this case, the two numbers are 165 and N, the GCF is 3 and the LCM is 15,015. Plug these values into the equation shown above in bold.

\(165 N = 3 \times 15,015\). Divide both sides by 165 to find N: N = \(\frac{3 \times 15015}{165} = \) 273

The property can also be used to find the LCM of two numbers if you know the GCF. For instance, if you were asked to find the GCF and LCM of 24 and 30. You can easily find the GCF, which is 6. To find the LCM, multiply the two numbers together, and divide by the GCF. (This should make sense to you intuitively if you think about it: You wouldn't list the GCF twice as you build the LCM. Also, the GCF will cancel into either of the two numbers since it is a factor of each.) So, the LCM(24, 30) = \((24 \cdot 30) \div 6 = 120\).

Exercise 13

If GCF(1176, 288) = 24, find the LCM(1176, 288)

Exercise 14

Find X if GCF(2940, X) = 105 and LCM(2940, X) = 79,380

Exercise 15

If the greatest common factor of 3,211 and another number is 247 and the least common multiple of the same two numbers is 48,165, then what is the other number?

Exercise 16

If you aren't given at least one of the numbers, there might be more that one possible solution. Figure out the possibilities for a and b if all you know is GCF(a, b) = 2 and LCM(a, b) = 20

The next few problems are a review of GCF and LCM. You now have several methods you can use to find the GCF and LCM.

17-20 Find the greatest common factor of each of the following pairs of numbers using prime factorization, the Old Chinese Method or the Euclidean Algorithm. Then, find the LCM of each pair. Show all work.

Exercise 17

a. GCF (693, 546) = _______

b. LCM (693, 546) = _______

Exercise 18

a. GCF (2117, 2555) = _______

b. LCM (2117, 2555) =

Exercise 19

a. GCF (1369, 10693) = ______

b. LCM (1369, 10693) =

Exercise 20

a. GCF (24300, 14406) = _______

b. LCM (24300, 14406) =

Exercise 21

Make up a problem where the GCF of 2 different 3-digit numbers is 32. For instance, GCF (x, y) = 32. Find an x and y that will work.

Exercise 22

Make up a problem where the GCF of two different 4-digit numbers is 32. In other words, find 2 numbers, a and b, such that GCF (a, b) = 32.

Exercise 23

Make up a problem where the GCF of 2 different 3-digit numbers is 35. For instance, GCF (x, y) = 35. Find an x and y that will work.

Exercise 24

Make up a problem where the GCF of two different 4-digit numbers is 28. In other words, find 2 numbers, a and b, such that GCF (a, b) = 28.

All even numbers are multiples of 2. Therefore, every even number can be written as the product of 2 and an integer. Symbolically, we can write every even number can be written in the form: 2k, where k is an integer. For example, 12 = 2(6), 20 = 2(10), 58 = 2(29), etc.

All odd numbers can be written as one more than an even number. Since an even number can be written as 2k, then symbolically, we write that every odd number can be written in the form: 2k + 1, where k is an integer. For example, 15 = 2(7) + 1, 41 = 2(20) + 1, etc.

Any integer that can be written in the form 2k is even and any integer that cannot be written in the form 2k is not even. Any integer that can be written in the form 2k + 1 is odd and any integer that cannot be written in the form 2k + 1 is not odd.

We'll be doing some proofs about even and odd numbers. The only way to express an even number, in general, is by 2k. The variable can be any letter. If you want to express more than one even number, you must use a new variable like 2m or 2n. The same is true for odd numbers.

For the examples and exercises that follow, assume all variables are integers.

EXAMPLES: State which of the following always represents an even number, which of the following always represents an odd number, and which are sometimes even and sometimes odd.

Example 1: 6n+14

6n + 14

Solution

6n + 14 = 2(3n + 7), which is in the form of an even number. Therefore, 6n + 14 will always represent an even number (since n is an integer).

Example 2: 4n+23

4n + 23

Solution

4n + 22 + 1 = 2(2n + 11) + 1, which is in the form of an odd number. Therefore, 6n + 14 will always represent an odd number.

Example 3: 5n+2

5n + 2

Solution

It is impossible to write 5n + 2 in the form 2k or 2k + 1. Therefore, it can't be determined. It is sometimes even and sometimes odd.

Note: You can verify these answers by plugging in an even number for n and then an odd number for n, and see if the conclusion makes sense. In example 1, if n = 2, then 6n + 14 = 6(2) + 14 = 28 (even). If n = 3, then 6(3) + 14 = 32 (even). So, the result was even when n was replaced by either an even or an odd number. Do the same verification for example 2 and 3 in the space below:

Exercise 25

State which of the following always represents an even number, which of the following always represents an odd number, and which are sometimes even and sometimes odd. Justify your answer.

a. 8n + 20

b. 10k + 9

c. 5x + 2

Example 1

Formally prove that the sum of two odd numbers is even.

IMPORTANT Note: Don't define the two odd numbers to be the same odd number. You must be general, and assume they may be two different odd numbers! Use different variables to be the most general.

Solution

Let 2n+1 = one odd number, and let 2m+1 = another odd number.

The sum is: 2n+1 + 2m+1= 2n+2m+2 = 2(n+m+1), which is in the form of an even number. Therefore, the sum of 2 odd numbers is even.

Example 2

Formally prove that the product of two odd numbers is odd.

Solution

Let 2n+1 = one odd number, and let 2m+1 = another odd number.

The sum is: (2n+1) (2m+1)= 4nm + 2m + 2n + 1 = 2(2nm + n + m) +1, which is in the form of an odd number. Therefore, the product of 2 odd numbers is odd.

Exercise 26

Formally prove that the sum of two even numbers is even.

Exercise 27

Formally prove that the sum of two odd numbers is even.

Exercise 28

Formally prove that the sum of an even number and an odd number is odd.

Exercise 29

Formally prove that the product of two even numbers is even.

Exercise 30

Formally prove that the product of two odd numbers is odd.

Exercise 31

Formally prove that the product of an even number and an odd number is even.

We are going to explore a way to find the sum of several consecutive whole numbers.

Example 1

1 + 2 + 3 + 4 + 5 + 6

Example 2

The sum of the first 100 counting numbers would take a long time to write out and compute. We write it in the following way: 1 + 2 + 3 + \(\dots\) + 98 + 99 + 100

Example 3

55 + 56 + 57 + \(\dots\) + 128 + 129 + 130

The first example is fairly easy to compute. But as more and more numbers are added, the computation becomes cumbersome. The first two examples start with the number, 1. Our first goal will be to find a pattern, and then a formula for adding any set of consecutive counting numbers starting with 1.

Even though we know the answer to example 1, we'll use that to find a pattern for the sum for other sums. Let X = the sum we are looking for (1 + 2 + 3 + 4 + 5 + 6). Notice what happens if X is written down twice – first in ascending order, then in descending order – and then the two rows are added by adding lined-up columns:

\(\begin{aligned} X = 1 + 2 + 3 + 4 + 5 + 6 \\ + \underline{X} = \underline{6} + \underline{5} + \underline{4} + \underline{3} + \underline{2} + \underline{1} \\ 2X = 7 + 7 + 7 + 7 + 7 + 7 \end{aligned}\)

The left side equals 2X, which is twice the actual sum we want. How many columns of numbers are on the right hand side of the equals sign? _____ Note: the number of columns is the same as the amount of numbers in the actual sum we are trying to find. What does each column on the right side of the equals sign add up to? _____ Since the right hand side of the equal sign is repeated addition, you can obtain the answer by using multiplication. What multiplication problem is this? _________ Since the left side equals the right side (2X = 42), then X = 21. Even if you didn't represent the sum using a variable, you would divide the right side by 2 because the sum is twice as large since the numbers in the sum were added twice.

Let's use this same technique to add the first 100 consecutive counting numbers. Let N = the actual sum. You fill in the third row by adding the left side, and then adding all of the columns on the right side.

\(\begin{aligned} N = && 1 && + && 2 && + && 3 &&+ && \dots && + && 98 && + && 99 + && 100 \\ + \underline{N} = && \underline{100} && +&& \underline{99} && + && \underline{98} && + && \dots && + && \underline{3} && + && \underline{2} + && \underline{1} \end{aligned}\)

How many columns (it's the same answer as the amount of numbers in the sum) are there on the right? ______ Since each column adds up to the same number, this is repeated addition. State the number that the right side adds up to: ___________ That is twice as big as the actual sum, so what does the sum (1 + 2 + 3 + \(\dots\) + 98 + 99 + 100) equal? ______

Hopefully, you got the answer of 5,050!

Exercise 32

Use the previous technique to find the sum of the first 80 counting numbers. Show work

Let's try to find a formula for finding the first n counting numbers using the same technique. Before writing the sum, what is the counting number preceding n? _______ What is the counting number preceding that number? ______

Let X = the sum of the first n counting numbers. Below, we'll use the same techique to find the sum. Fill in the sum on the left side of the equals side and the sum of each column on the right.

What does each column on the right add up to? ________ Again, the right side is a repeated addition again. Multiply the number of columns (which is equal to the amount of numbers in the sum of the first n counting numbers) by the number each column adds up to.

What does the right side equal? _____________ This is twice as large as the actual sum we want.

What does the actual sum of the first n counting numbers equal? _____________

Hopefully, you got this answer: \(\frac{n(n+1)}{2}\)

Of course, the answer depends on n. Let's using this formula to compute the sum of the first six counting numbers, which was the first example we did. In this example, n = 6. So, plugging n = 6 into the formula, we get \((6 \cdot 7)\) / 2 = 21. Same answer!

Exercise 33

Use the formula to find the sum of the first 80 counting numbers.

Exercise 34

Use the formula to find this sum: 1 + 2 + 3 + \(\dots\) + 248 + 249 + 250.

What if you wanted to find this sum? 55 + 56 + 57 + \(\dots\) + 128 + 129 + 130

If you used the formula, then you would have the sum of all the numbers from 1 to 130 instead of only the ones from 55 on. One strategy is to use the formula and then subtract off the extra numbers you added. For instance, if you add all the numbers from 1 - 130, the extra numbers added that are not part of the sum are: 1 + 2 + 3 + \(\dots\) + 52 + 53 + 54. But this sum is easy to compute since we can use the formula to get this sum! So here is the strategy:

55 + 56 + 57 + \(\dots\) + 128 + 129 + 130

= (the sum of the first 130 counting numbers) – (the sum of the first 54 counting numbers)

= (1 + 2 + 3 + \(\dots\) + 128 + 129 + 130) – (1 + 2 + 3 + \(\dots\) + 52 + 53 + 54)

= \(\frac{130(131)}{2} - \frac{54(55)}{2}\) = 8,515 - 1,485 = 7,030

Example

Find the sum: 81 + 82 + 83 + \(\dots\) + 198 + 199 + 200

Solution

Subtract the sum of the first 80 counting numbers from the sum of the first 200 counting numbers: 200(201)/2 – 80(81)/2 = 20,100 – 3,240 = 16,860.

Exercise 35

Find the following sums using the strategy just shown. Show work.

a. 51 + 52 + 53 + \(\dots\) + 98 + 99 + 100

b. 146 + 147 + 148 + \(\dots\) + 561 + 562 + 563

c. 500 + 501 + 502 + \(\dots\) + 798 + 799 + 800

There is a different strategy we can use to find the sum of consecutive whole numbers that do not begin with the number, 1. Let's look at another way to compute the sum of these whole numbers: 55 + 56 + 57 + \(\dots\) + 128 + 129 + 130. We'll begin by using the same type of strategy we used at the beginning of this topic. First, let X = the sum. Write the sum down twice – first in ascending order, then in descending order – and then add the two rows by adding the individual lined-up columns. This is shown on the next page.

\(\begin{aligned} X = & 55 + & 56& + & 57 &+ & \dots &+& 128 &+& 129 &+ &130 \\ \underline{X} =& \underline{130} + &\underline{129}& +& \underline{128} &+ & \dots &+ & \underline{57} &+ & \underline{56}& + \underline{55} \\ 2X = &185 + & 185& +& 185 &+ &\dots &+& 185 &+ &185 &+ &185 \end{aligned}\)

At this point, we can see the similarity to how we derived the sum of the first n counting numbers, but there is one big difference here. It's not clear exactly how many addends of 185 are on the right-hand side of the equals sign. Most people will say that there are 130 – 55, or 75 of them, but actually that reasoning (subtracting the first number from the last number) is not correct. For instance, if you were adding the numbers from 1 to 130, most people will agree that there are 130 numbers being added, which is NOT the same answer you would get if you subtracted the first number from the last number since 130 – 1 only equals 129. Look at simpler example: 17 + 18 + 19 + 20. It's clear there are 4 numbers in the sum, but if you did the subtraction 20 – 17, you would get 3, which is the incorrect answer. One way to figure out how many numbers are in the sum is to decide how many numbers are missing from the sum if it did begin with 1. Look at the sum again: 17 + 18 + 19 + 20 has the first 16 numbers missing, so instead of 20 numbers in the sum (which is how many there would be if we started at 1), there are 20 – 16 numbers in the sum. Okay, back to figuring out how many numbers are actually in the sum above.

How many numbers are in the sum: 55 + 56 + 57 + \(\dots\) + 128 + 129 + 130? _______

So, the right side of the equation has 76 185's added together, which is 76 \(\cdots\) 185, which equals 14,060. But, this is twice as big as the actual sum, so after dividing by 2, we get the actual sum of 7,030. This is the same answer we got when we did this problem on the previous page using a different strategy.

Exercise 36

Find the following sums using the strategy just shown. Show work.

a. 51 + 52 + 53 + \(\dots\) + 98 + 99 + 100

b. 146 + 147 + 148 + \(\dots\) + 561 + 562 + 563

c. 500 + 501 + 502 + \(\dots\) + 798 + 799 + 800

d. Challenge: k + (k + 1) + (k + 2) + \(\dots\) + (n - 2) + (n - 1) + n

So far, you have learned how to easily find the sum of several consecutive whole numbers. Let's take it one step further. What if the sum you want to find are numbers that are not consecutive. Depending on the the sequence of numbers, the sum may or may not be easy to find. We are going to look at sums that have consecutive numbers added together in disguise. For instance, look at the following sum:

7 + 14 + 21 + \(\dots\) + 693 + 700

Exercise 37

What do you notice about the numbers added together?

Exercise 38

Hopefully, you noticed that all of the numbers were multiples of seven, or perhaps you noticed you add seven to each number to get the next number. Take the sum and rewrite the problem by factoring out a 7; just fill in the blanks below:

7 + 14 + 21 + \(\dots\)+ 693 + 700 = 7 ( ____ + ____ + ____ + \(\dots\) + ____ + ____ )

Exercise 39

Now, you should be able to figure out the sum of the numbers in parentheses. Show your work to figure out the sum. Then answer a, b and c.

a. What is the sum of the numbers in parentheses? __________

b. So, the sum 7 + 14 + 21 + 28 + \(\dots\) + 700 becomes 7 _________

c. Therefore, 7 + 14 + 21 + 28 + \(\dots\) + 700 = _______________

Exercise 40

Find the following sums. Show your work.

a. 8 + 16 + 24 + \(\dots\) + 992 + 1000 = ____________

b. 11 + 22 + 33 + \(\dots\) + 935+ 946 = _____________

c. 20 + 40 + 60 + 80 + \(\dots\) + 2980 + 3000 = _____________

Okay, just one more twist...this puts it all together. Consider this sum:

112 + 116 + 120 + \(\dots\) + 524 + 528

Exercise 41

This time, what do you notice about the numbers added together?

Exercise 42

Hopefully, you noticed all the numbers were multiples of four, or that you added four to each number to get the next number. Take the sum and rewrite the problem by factoring out a 4; just fill in the blanks below:

112 + 116 + 120 + \(\dots\) + 524 + 528 = 4 ( ____ + ____ + ____ + \(\dots\) + _____ + _____ )

Exercise 43

Now, you should be able to figure out the sum of the numbers in parentheses. Note that the sum does not start with a 1. Show your work to figure out the sum. Then answer a, b and c.

a. What is the sum of the numbers in parentheses? __________

b. So, the sum 112 + 116 + 120 + \(\dots\) + 524 + 528 becomes 4 _________

c. Therefore, 112 + 116 + 120 + \(\dots\) + 524 + 528 = _______________

Exercise 44

Find the following sums. Show your work.

a. 85 + 90 + 95 + \(\dots\) + 735 + 740 = ____________

b. 430 + 473 + 516 + \(\dots\) + 2838+ 2881 = _____________

Here are some problems for you to figure out what numbers are on the number line. For each problem, figure out where on the number line (what number) the man might be standing. Where there is more than one possibility, only list numbers between 1 and 1000.

Exercise 45

Exercise 46

Exercise 47

Exercise 48

Exercise 49

Exercise 50

Exercise 51

Exercise 52

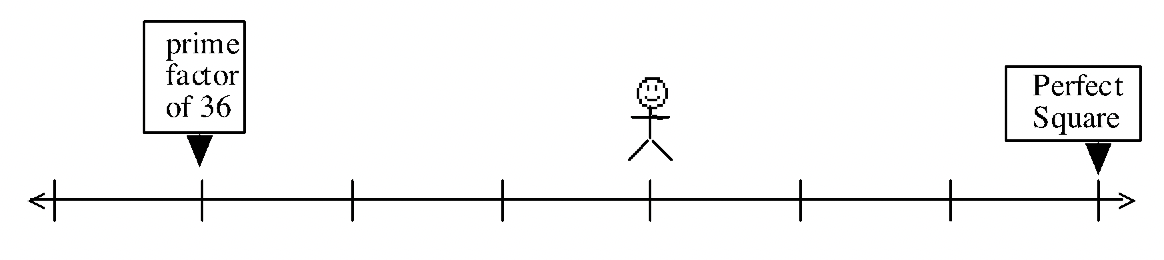
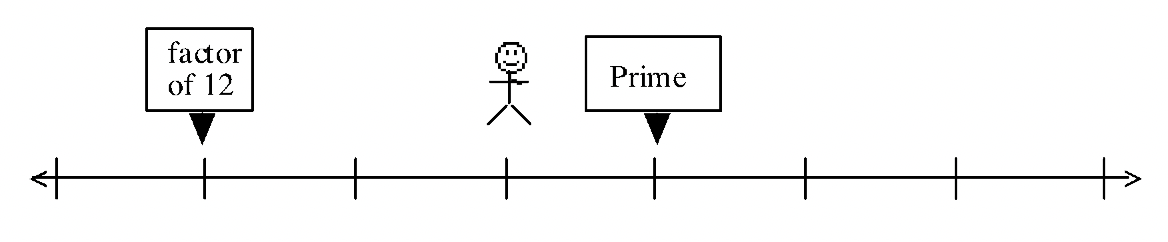
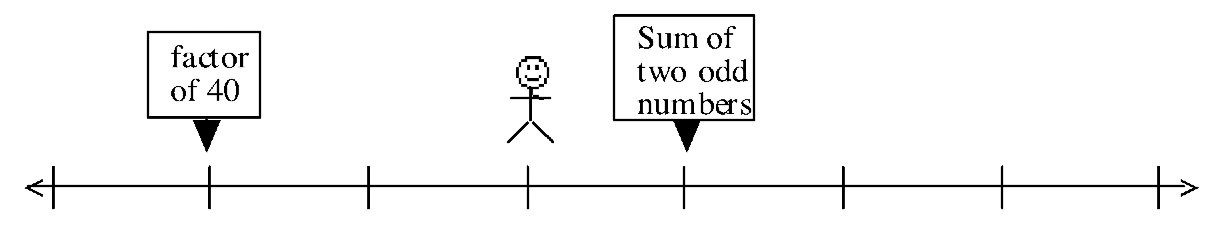
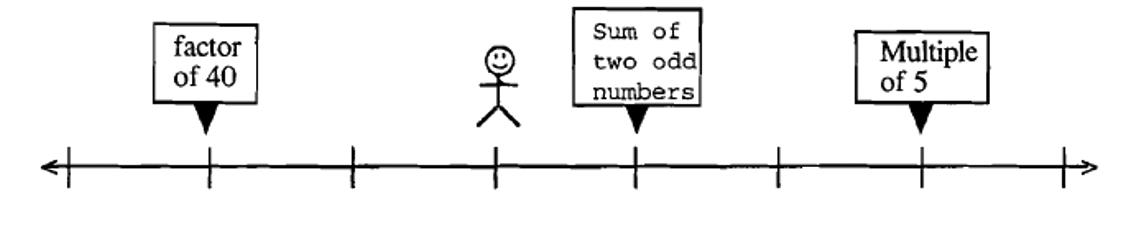
(There are actually nine possibilities between 1 and 1000 for this problem.)

Exercise 53

Exercise 54

Exercise 55

Exercise 56

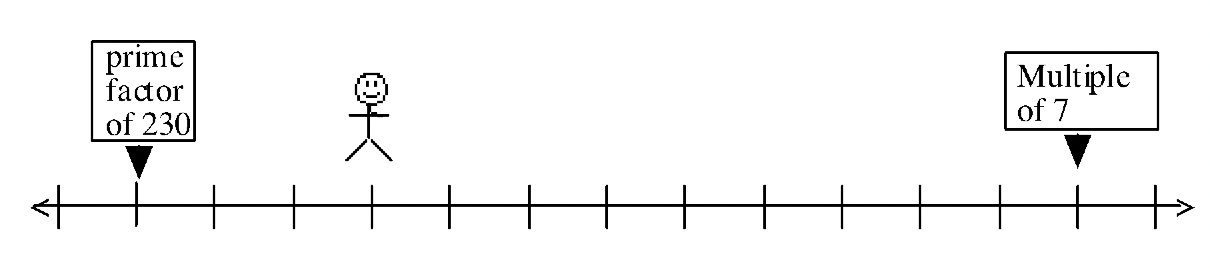
Which of the clues in #53 was was not needed if the man is only standing on one single number? #54 and #55 should help you answer this. For instance, if you got more than one possibility for #54 or #55, then that problem didn't provide enough clues. For the one that gave exactly one possibility, that was enough clues, so the clue from #53 that was missing wasn't really needed.

Exercise 57

Exercise 58

Exercise 59

Exercise 60

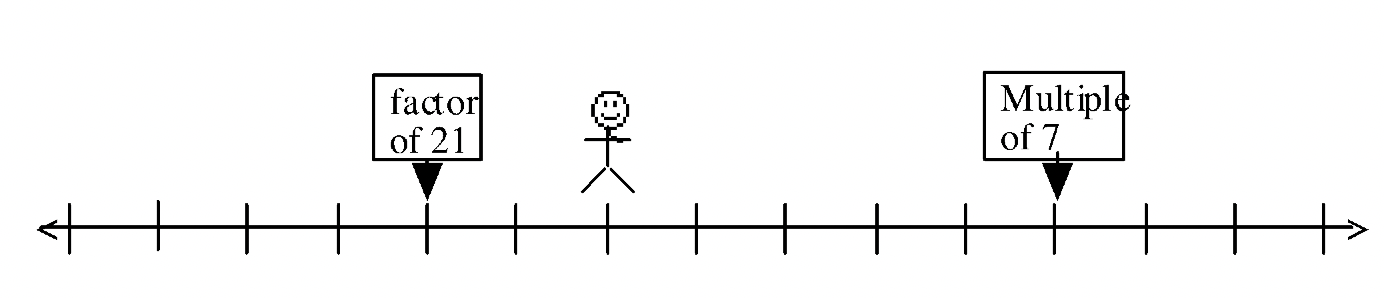
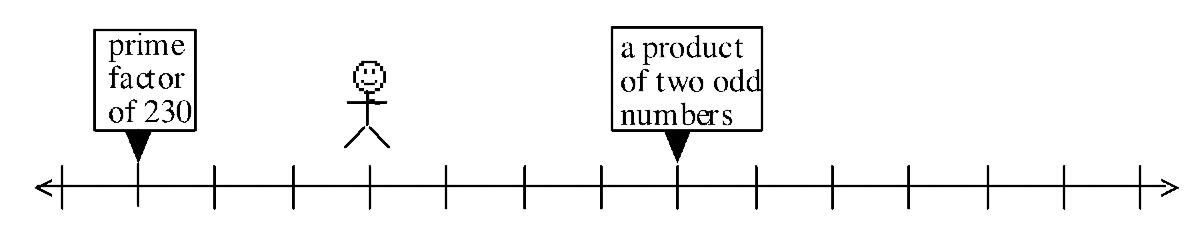
If the man in exercise #59 is standing on only one number in this problem, are all three clues given needed?

Yes or No:_________ Explain: