1.1: Tiling the Plane
- Page ID
- 39427
Lesson
Let's look at tiling patterns and think about area.
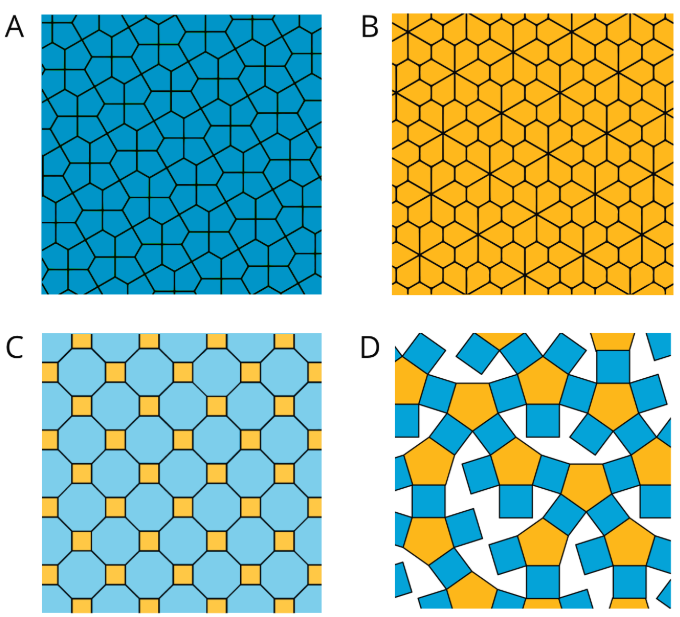
Exercise \(\PageIndex{1}\): Which One Doesn't Belong: Tilings
Which pattern doesn’t belong?
Exercise \(\PageIndex{2}\): More Red, Green, or Blue?
Your teacher will assign you to look at Pattern A or Pattern B.
In your pattern, which shapes cover more of the plane: blue rhombuses, red trapezoids, or green triangles? Explain how you know.
You may use the sliders and the shapes in this applet to help. Explore what you can see or hide, and what you can move or turn.
Are you ready for more?
On graph paper, create a tiling pattern so that:
- The pattern has at least two different shapes.
- The same amount of the plane is covered by each type of shape.
Summary
In this lesson, we learned about tiling the plane, which means covering a two-dimensional region with copies of the same shape or shapes such that there are no gaps or overlaps.
Then, we compared tiling patterns and the shapes in them. In thinking about which patterns and shapes cover more of the plane, we have started to reason about area.
We will continue this work, and to learn how to use mathematical tools strategically to help us do mathematics.
Glossary Entries
Definition: Area
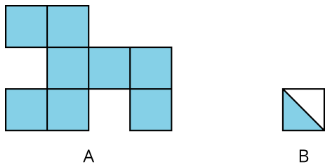
Area is the number of square units that cover a two-dimensional region, without any gaps or overlaps.
For example, the area of region A is 8 square units. The area of the shaded region of B is \(\frac{1}{2}\) square unit.
Definition: Region
A region is the space inside of a shape. Some examples of two-dimensional regions are inside a circle or inside a polygon. Some examples of three-dimensional regions are the inside of a cube or the inside of a sphere.
Practice
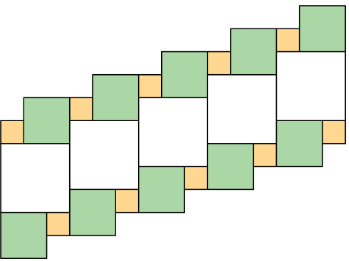
Exercise \(\PageIndex{3}\)
Which square—large, medium, or small—covers more of the plane? Explain your reasoning.
Exercise \(\PageIndex{4}\)
Draw three different quadrilaterals, each with an area of 12 square units.

Exercise \(\PageIndex{5}\)
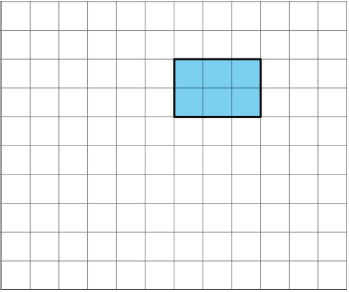
Use copies of the rectangle to show how a rectangle could:
- tile the plane.
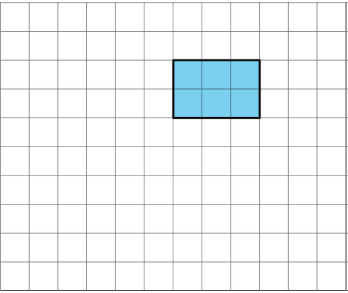
- not tile the plane.
Exercise \(\PageIndex{6}\)
The area of this shape is 24 square units. Which of these statements is true about the area? Select all that apply.
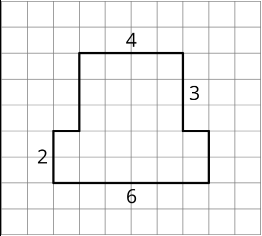
- The area can be found by counting the number of squares that touch the edge of the shape.
- It takes 24 grid squares to cover the shape without gaps and overlaps.
- The area can be found by multiplying the sides lengths that are 6 units and 4 units.
- The area can be found by counting the grid squares inside the shape.
- The area can be found by adding \(4\times 3\) and \(6\times 2\).
Exercise \(\PageIndex{7}\)
Here are two copies of the same figure. Show two different ways for finding the area of the shaded region. All angles are right angles.
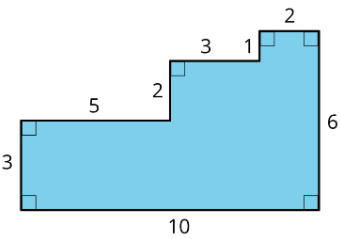
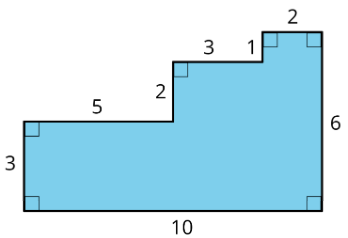
Exercise \(\PageIndex{8}\)
Which shape has a larger area: a rectangle that is 7 inches by \(\frac{3}{4}\) inch, or a square with side length of \(2\frac{1}{2}\) inches? Show your reasoning.


