Skip to main content
Mathematics LibreTexts

2.3: Area of Parallelograms

  1. Last updated
  2. Save as PDF
  • Page ID
    39637

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lesson

    Let's practice finding the area of parallelograms.

    Exercise \(\PageIndex{1}\): Missing Dots

    clipboard_e9ada10e020939c31049c757a6fca015f.png
    Figure \(\PageIndex{1}\)

    How many dots are in the image?

    How do you see them?

    Exercise \(\PageIndex{2}\): More Areas of Parallelograms

      1. Calculate the area of the given figure in the applet. Then, check if your area calculation is correct by clicking the Show Area checkbox.
      2. Uncheck the Area checkbox. Move one of the vertices of the parallelogram to create a new parallelogram. When you get a parallelogram that you like, sketch it and calculate the area. Then, check if your calculation is correct by using the Show Area button again.
      3. Repeat this process two more times. Draw and label each parallelogram with its measurements and the area you calculated.
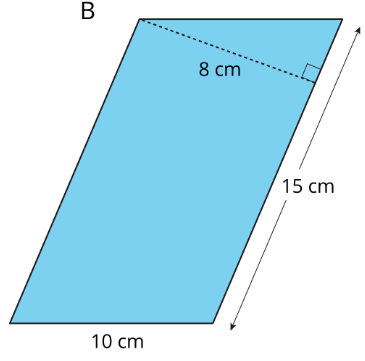
    2. Here is Parallelogram B. What is the corresponding height for the base that is 10 cm long? Explain or show your reasoning.
    clipboard_e744cff7e207fdc40d671e85fb43e0afc.png
    Figure \(\PageIndex{2}\)
    1. Here are two different parallelograms with the same area.
      1. Explain why their areas are equal.
      2. Drag points to create two new parallelograms that are not identical copies of each other but that have the same area as each other. Sketch your parallelograms and explain or show how you know their areas are equal. Then, click on the Check button to see if the two areas are indeed equal.

    Are you ready for more?

    Here is a parallelogram composed of smaller parallelograms. The shaded region is composed of four identical parallelograms. All lengths are in inches.

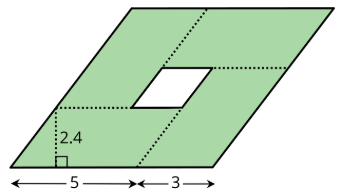
    clipboard_e25bd683eeeed71b1c1e3ca723f286f23.png
    Figure \(\PageIndex{3}\): Parallelogram composed of smaller parallelograms. The shaded region is composed of four identical parallelograms, for each, base = 5, height = 2 and 4 tenths, slant length = 3.

    What is the area of the unshaded parallelogram in the middle? Explain or show your reasoning.

    Summary

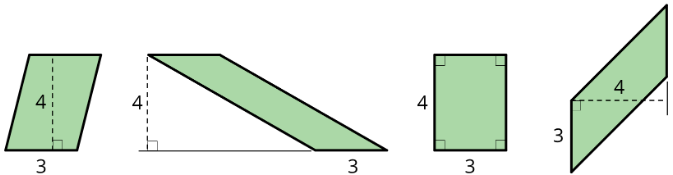
    Any pair of base and corresponding height can help us find the area of a parallelogram, but some base-height pairs are more easily identified than others.

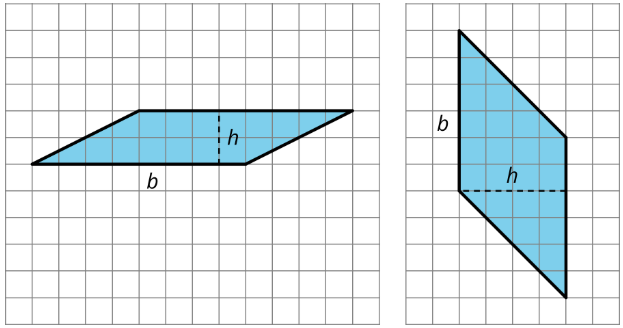
    When a parallelogram is drawn on a grid and has horizontal sides, we can use a horizontal side as the base. When it has vertical sides, we can use a vertical side as the base. The grid can help us find (or estimate) the lengths of the base and of the corresponding height.

    clipboard_e62eb11b1598e9b44704f8e7fb2ae0fe9.png
    Figure \(\PageIndex{4}\): Two parallelograms drawn on two grids. First parallelogram, 2 horizontal sides each 8 units long, 2 slanted sides that rise 2 vertical units over 4 horizontal units. Bottom horizontal side labeled, b. A 2-unit perpendicular segment labeled, h, connects the horizontal sides. Second parallelogram, 2 vertical sides each 6 units long, 2 slanted sides that rise 4 vertical units over 4 horizontal units. The left vertical side is labeled, b. A 4-unit perpendicular segment labeled, h, connects one vertex of the vertical side to a point on the other vertical side.

    When a parallelogram is not drawn on a grid, we can still find its area if a base and a corresponding height are known.

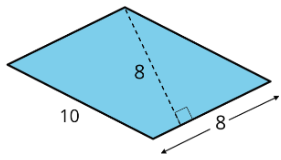
    clipboard_eb590ffece5ff59bd7307ac908c793abc.png
    Figure \(\PageIndex{5}\)

    In this parallelogram, the corresponding height for the side that is 10 units long is not given, but the height for the side that is 8 units long is given. This base-height pair can help us find the area.

    Regardless of their shape, parallelograms that have the same base and the same height will have the same area; the product of the base and height will be equal. Here are some parallelograms with the same pair of base-height measurements.

    clipboard_eb9cd76ee57f696d5983ea1ce75dbd7e4.png
    Figure \(\PageIndex{6}\)

    Glossary Entries

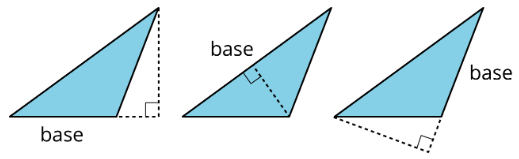
    Definition: base (of a parallelogram or triangle)

    We can choose any side of a parallelogram or triangle to be the shape’s base. Sometimes we use the word base to refer to the length of this side.

    clipboard_efdc2d1802033a1596e2069df32cf5ce3.png
    Figure \(\PageIndex{7}\)

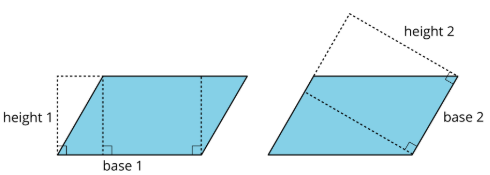
    Definition: height (of a parallelogram or triangle)

    The height is the shortest distance from the base of the shape to the opposite side (for a parallelogram) or opposite vertex (for a triangle).

    We can show the height in more than one place, but it will always be perpendicular to the chosen base.

    clipboard_e96534d8024d2edc81ecf56bfbbda66ab.png
    Figure \(\PageIndex{8}\)

    Definition: Parallelogram

    A parallelogram is a type of quadrilateral that has two pairs of parallel sides.

    Here are two examples of parallelograms.

    clipboard_e63643e0f76082a51a15180251ba0759c.png
    Figure \(\PageIndex{9}\): Two parallelograms with the angles and side lengths provided. On the left, Top and bottom sides = 5 units. Left and right sides = 4.24 units. Top left and bottom right angles = 135 degrees. Top right and bottom left angles = 45 degrees. On the right, Top and bottom sides = 9.34 units. Left and right sides = 4 units. Top left and bottom right angles = 27.2 degrees. Top right and bottom left angles = 152.8 degrees.

    Definition: Quadrilateral

    A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.

    Practice

    Exercise \(\PageIndex{3}\)

    Which three of these parallelograms have the same area as each other?

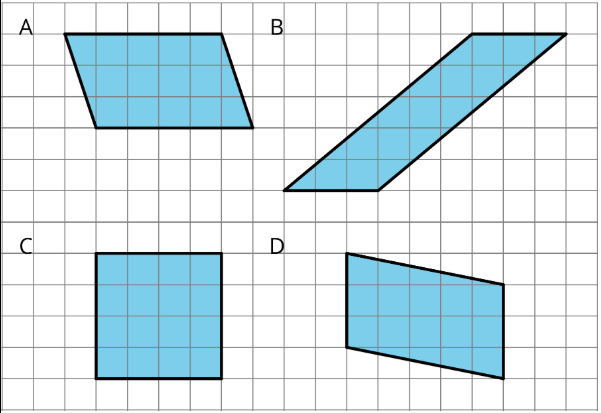
    clipboard_e9e002028eb2fc18176bbaa1deacfe2c4.png
    Figure D, the left and right sides are each 3 units, and the top and bottom sides descend 1 unit as they move right 5 units.
    1. A
    2. B
    3. C
    4. D

    Exercise \(\PageIndex{4}\)

    Which pair of base and height produces the greatest area? All measurements are in centimeters.

    1. \(b=4, h=3.5\)
    2. \(b=0.8, h=20\)
    3. \(b=6, h=2.25\)
    4. \(b=10, h=1.4\)

    Exercise \(\PageIndex{5}\)

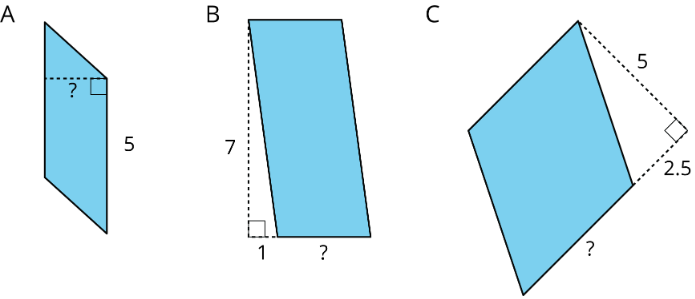
    Here are the areas of three parallelograms. Use them to find the missing length (labeled with a "?") on each parallelogram.

    1. 10 square units
    2. 21 square units
    3. 25 square units
    clipboard_e53c91a5ccaa0a6152875207bc56708a3.png
    Figure \(\PageIndex{11}\): Three parallelograms labeled A, B, C. Parallelogram A, right side = 5 units, height = question mark. Parallelogram B, bottom side = question mark. Right triangle drawn outside of parallelogram, base = 1 unit, height = 7 units. Parallelogram C, bottom side = question mark. Right triangle drawn outside of parallelogram, base = 2.5 units, height = 5 units.

    Exercise \(\PageIndex{6}\)

    The Dockland Building in Hamburg, Germany is shaped like a parallelogram.

    clipboard_eaf5c857c895721ab1a8287ebae243377.png
    Figure \(\PageIndex{12}\): Architecture Port Elbe Hamburg Building, by Max Pixel. Public Domain. freegreatpicture.com. Source.

    If the length of the building is 86 meters and its height is 55 meters, what is the area of this face of the building?

    Exercise \(\PageIndex{7}\)

    Select all segments that could represent a corresponding height if the side \(m\) is the base.

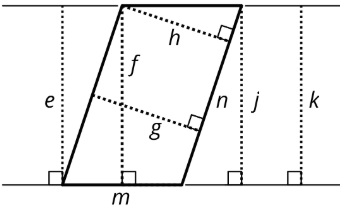
    clipboard_e648066e5ccb62cd8ba5de8c107c9cdca.png
    Figure \(\PageIndex{13}\)
    1. e
    2. f
    3. g
    4. h
    5. j
    6. k
    7. n

    (From Unit 1.2.2)

    Exercise \(\PageIndex{8}\)

    Find the area of the shaded region. All measurements are in centimeters. Show your reasoning.

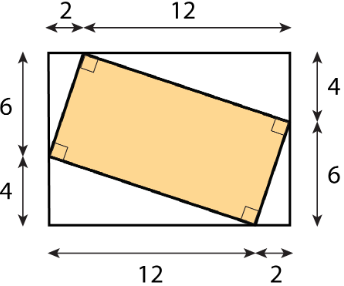
    clipboard_ee6ac20adfc0d1f15faeeedf3c6c57c63.png
    Figure \(\PageIndex{14}\)

    (From Unit 1.1.3)

    This page titled 2.3: Area of Parallelograms is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Illustrative Mathematics via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.