Skip to main content
Mathematics LibreTexts

3.2: Area of Triangles

  1. Last updated
  2. Save as PDF
  • Page ID
    39640

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lesson

    Let's use what we know about parallelograms to find the area of triangles.

    Exercise \(\PageIndex{1}\): Composing Parallelograms

    Here is Triangle M.

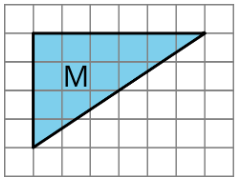
    clipboard_e300ecc70432335a53380333248f47bfb.png
    Figure \(\PageIndex{1}\)

    Han made a copy of Triangle M and composed three different parallelograms using the original M and the copy, as shown here.

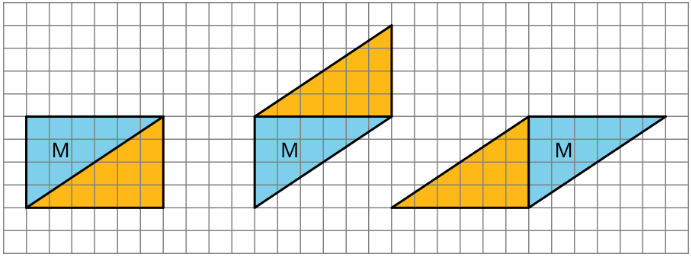
    clipboard_ed4626aa95686431f75e8e1689ed91b9f.png
    Figure \(\PageIndex{2}\): 3 different parallelograms on a grid composed of Triangle M and a copy. First parallelogram, Triangle M and a copy along the slanted side of the triangle. Second parallelogram, Triangle M and a copy along the horizontal side of the triangle. Third parallelogram, Triangle M and a copy along the vertical side of the triangle.
    1. For each parallelogram Han composed, identify a base and a corresponding height, and write the measurements on the drawing.
    2. Find the area of each parallelogram Han composed. Show your reasoning.

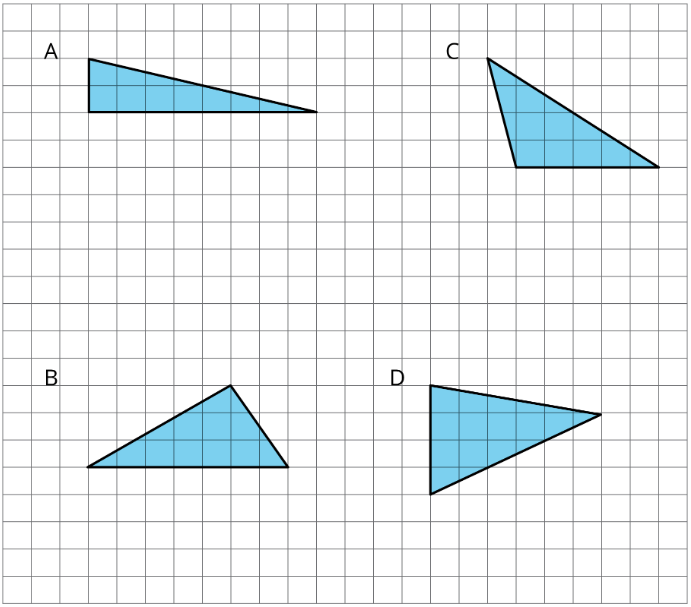
    Exercise \(\PageIndex{2}\): More Triangles

    Find the areas of at least two of these triangles. Show your reasoning.

    clipboard_eb988041da8effc916e888fa726aae645.png
    Figure \(\PageIndex{3}\)

    Exercise \(\PageIndex{3}\): Decomposing a Parallelogram

    1. Your teacher will give you two copies of a parallelogram. Glue or tape one copy of your parallelogram here and find its area. Show your reasoning.
    2. Decompose the second copy of your parallelogram by cutting along the dotted lines. Take only the small triangle and the trapezoid, and rearrange these two pieces into a different parallelogram. Glue or tape the newly composed parallelogram on your paper.
    3. Find the area of the new parallelogram you composed. Show your reasoning.
    4. What do you notice about the relationship between the area of this new parallelogram and the original one?
    5. How do you think the area of the large triangle compares to that of the new parallelogram: Is it larger, the same, or smaller? Why is that?
    6. Glue or tape the remaining large triangle to your paper. Use any part of your work to help you find its area. Show your reasoning.

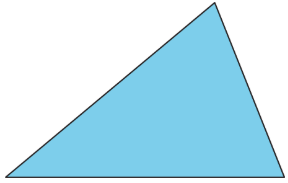
    Are you ready for more?

    Can you decompose this triangle and rearrange its parts to form a rectangle? Describe how it could be done.

    clipboard_e77c85c80c117ef45198723595d3621db.png
    Figure \(\PageIndex{4}\)

    Summary

    We can reason about the area of a triangle by using what we know about parallelograms. Here are three general ways to do this:

    • Make a copy of the triangle and join the original and the copy along an edge to create a parallelogram. Because the two triangles have the same area, one copy of the triangle has half the area of that parallelogram.
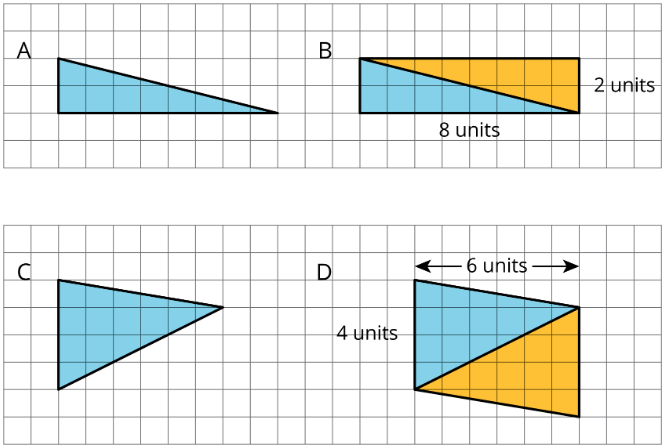
    clipboard_e57bce4079a7322ebf76cbbae36a023e2.png
    Figure C is another triangle, and figure D is the same triangle as figure C, with a copy along the edge of the original to create parallelogram. The left base of the parallelogram is labeled 4 units, and the height is labeled 6 units.

    The area of Parallelogram B is 16 square units because the base is 8 units and the height 2 units. The area of Triangle A is half of that, which is 8 square units. The area of Parallelogram D is 24 square units because the base is 4 units and the height 6 units. The area of Triangle C is half of that, which is 12 square units.

    • Decompose the triangle into smaller pieces and compose them into a parallelogram.
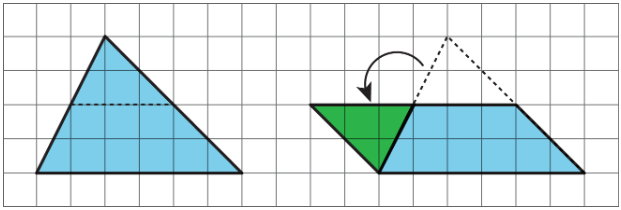
    clipboard_ee676c77ccee11349714425b81b2f2f7a.png
    Figure \(\PageIndex{6}\): Two images of a triangle. Image on right has a dashed line cutting off the top portion. Image on left has the cut off portion moved next to the bottom of the triangle to create a parallelogram. An arrow indicating that the cut off portion from other image was moved.

    In the new parallelogram, \(b=6\), \(h=2\), and \(6\cdot 2=12\), so its area is 12 square units. Because the original triangle and the parallelogram are composed of the same parts, the area of the original triangle is also 12 square units.

    • Draw a rectangle around the triangle. Sometimes the triangle has half of the area of the rectangle.
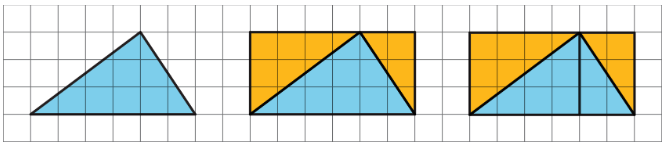
    clipboard_e97d94dc3e2aaff3a0d4ccb221e586ed4.png
    Figure \(\PageIndex{7}\)

    The large rectangle can be decomposed into smaller rectangles. The one on the left has area \(4\cdot 3\) or 12 square units; the one on the right has area \(2\cdot 3\) or 6 square units. The large triangle is also decomposed into two right triangles. Each of the right triangles is half of a smaller rectangle, so their areas are 6 square units and 3 square units. The large triangle has area 9 square units.

    Sometimes, the triangle is half of what is left of the rectangle after removing two copies of the smaller right triangles.

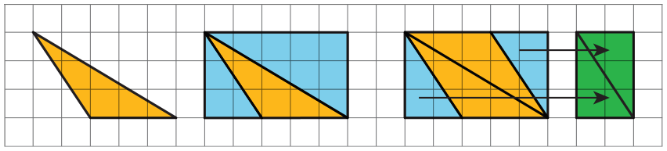
    clipboard_e5146c190a08ac4241f264b102a1628c7.png
    Figure \(\PageIndex{8}\): Three images of the same triangle. The first image is the triangle alone. The second is the triangle surrounded by a rectangle. The third image is of the triangle now with a copy composed into a parallelogram within the rectangle, with arrows drawing the remaining parts of the rectangle into a smaller rectangle.

    The right triangles being removed can be composed into a small rectangle with area \((2\cdot 3)\) square units. What is left is a parallelogram with area \(5\cdot 3-2\cdot 3\), which equals \(15-6\) or \(9\) square units. Notice that we can compose the same parallelogram with two copies of the original triangle! The original triangle is half of the parallelogram, so its area is \(\frac{1}{2}\cdot 9\) or \(4.5\) square units.

    Practice

    Exercise \(\PageIndex{4}\)

    To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.

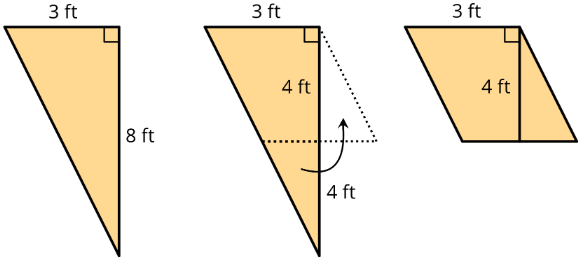
    clipboard_e920aad5791b6dd1e5cef9209a3891cae.png
    Figure \(\PageIndex{9}\): A triangle with one side labeled 3 feet and another side labeled 8 feet. A second image displays the same triangle with a dashed line bisecting the triangle so the side that was labeled 8 feet is now two pieces, each labeled 4 feet. An arrow indicates that the resulting smaller portion is rotated to create a parallelogram with a base of 3 feet and a height of 4 feet.

    Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram.

    clipboard_e63ad903c727e794e74463030fb2e9768.png
    Figure \(\PageIndex{10}\)
    1. Explain how Diego might use his parallelogram to find the area of the triangle.
    2. Explain how Jada might use her parallelogram to find the area of the triangle.

    Exercise \(\PageIndex{5}\)

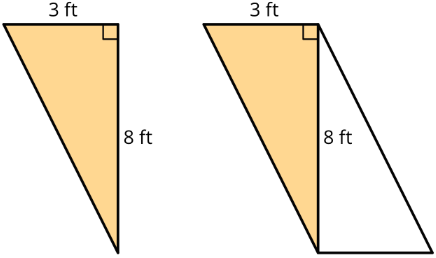
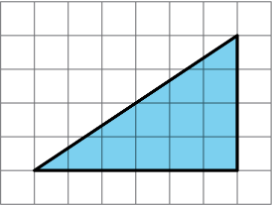
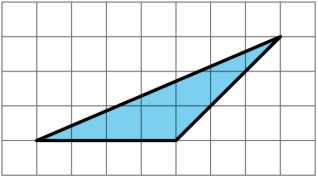
    Find the area of the triangle. Explain or show your reasoning.

    clipboard_eb079fc20285c2dab81a545c29e31a457.png
    Figure \(\PageIndex{11}\)
    clipboard_e51cc207318cbff7af8faca8aba737aca.png
    Figure \(\PageIndex{12}\)

    Exercise \(\PageIndex{6}\)

    Which of the three triangles has the greatest area? Show your reasoning. If you get stuck, try using what you know about the area of parallelograms.

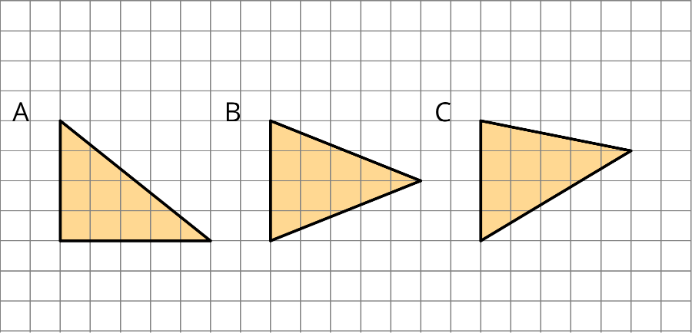
    clipboard_e32f66f9872198c0af663cf034b86817c.png
    Figure \(\PageIndex{13}\)

    Exercise \(\PageIndex{7}\)

    Draw an identical copy of each triangle such that the two copies together form a parallelogram. If you get stuck, consider using tracing paper.

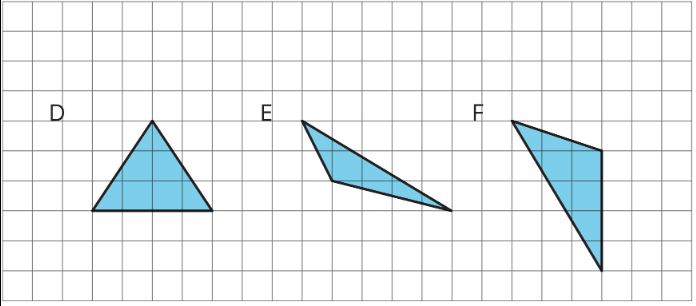
    clipboard_e2a92a2bf2f72df7218c6d15fb5956c76.png
    Figure \(\PageIndex{14}\)

    (From Unit 1.3.1)

    Exercise \(\PageIndex{8}\)

    1. A parallelogram has a base of 3.5 units and a corresponding height of 2 units. What is its area?
    2. A parallelogram has a base of 3 units and an area of 1.8 square units. What is the corresponding height for that base?
    3. A parallelogram has an area of 20.4 square units. If the height that corresponds to a base is 4 units, what is the base?

    (From Unit 1.2.3)

    This page titled 3.2: Area of Triangles is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Illustrative Mathematics via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.