3.3: Formula for the Area of a Triangle
- Page ID
- 39639
Lesson
Let's write and use a formula to find the area of a triangle.
Exercise \(\PageIndex{1}\): Bases and Heights of a Triangle
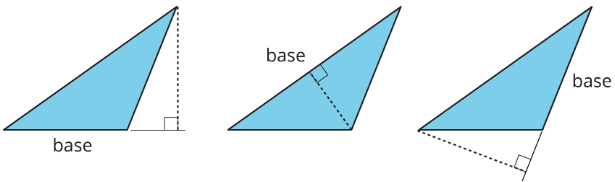
Study the examples and non-examples of bases and heights in a triangle.
- Examples: These dashed segments represent heights of the triangle.
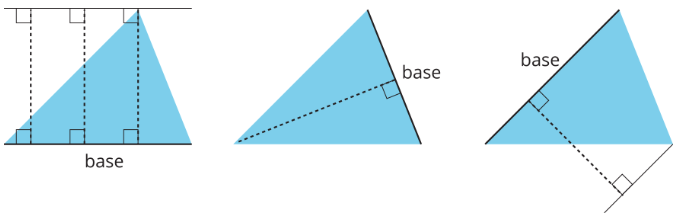
- Non-examples: These dashed segments do not represent heights of the triangle.
Select all the statements that are true about bases and heights in a triangle.
- Any side of a triangle can be a base.
- There is only one possible height.
- A height is always one of the sides of a triangle.
- A height that corresponds to a base must be drawn at an acute angle to the base.
- A height that corresponds to a base must be drawn at a right angle to the base.
- Once we choose a base, there is only one segment that represents the corresponding height.
- A segment representing a height must go through a vertex.
Exercise \(\PageIndex{2}\): Finding a Formula for Area of a Triangle
For each triangle:
- Identify a base and a corresponding height, and record their lengths in the table.
- Find the area of the triangle and record it in the last column of the table.
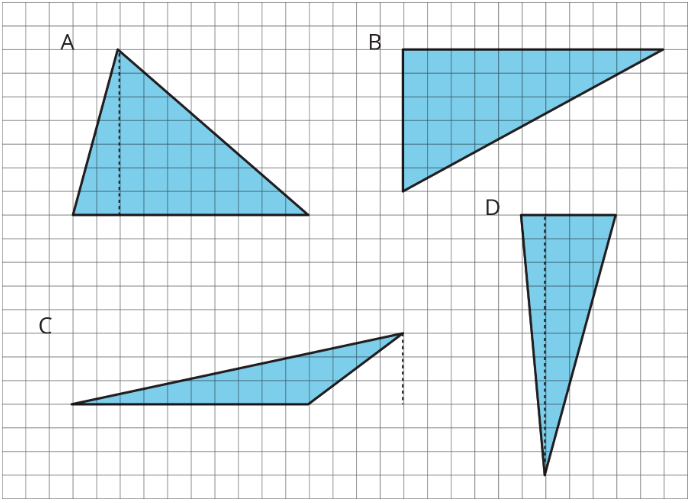
| triangle | base (units) | height (units) | area (square units) |
|---|---|---|---|
| A | |||
| B | |||
| C | |||
| D | |||
| any triangle | \(b\) | \(h\) |
In the last row, write an expression for the area of any triangle, using \(b\) and \(h\).
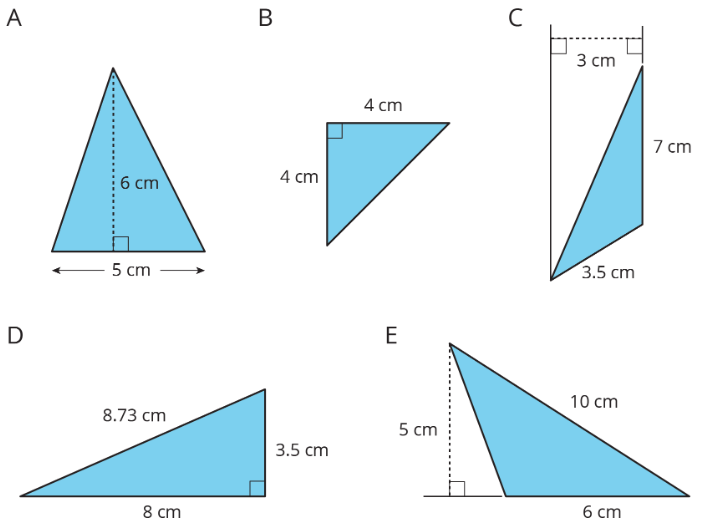
Exercise \(\PageIndex{3}\): Applying the Formula for Area of Triangles
For each triangle, circle a base measurement that you can use to find the area of the triangle. Then, find the area of any three triangles. Show your reasoning.
Summary
- We can choose any of the three sides of a triangle to call the base. The term “base” refers to both the side and its length (the measurement).
- The corresponding height is the length of a perpendicular segment from the base to the vertex opposite of it. The opposite vertex is the vertex that is not an endpoint of the base.
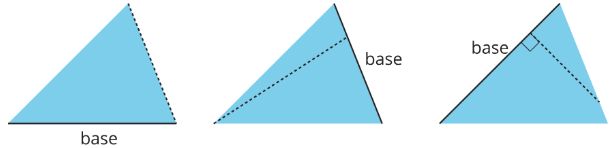
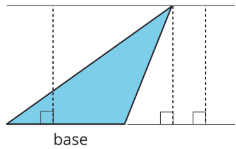
Here are three pairs of bases and heights for the same triangle. The dashed segments in the diagrams represent heights.
A segment showing a height must be drawn at a right angle to the base, but it can be drawn in more than one place. It does not have to go through the opposite vertex, as long as it connects the base and a line that is parallel to the base and goes through the opposite vertex, as shown here.
The base-height pairs in a triangle are closely related to those in a parallelogram. Recall that two copies of a triangle can be composed into one or more parallelograms. Each parallelogram shares at least one base with the triangle.
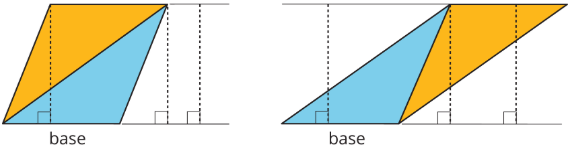
For any base that they share, the corresponding height is also shared, as shown by the dashed segments.
We can use the base-height measurements and our knowledge of parallelograms to find the area of any triangle.
- The formula for the area of a parallelogram with base \(b\) and height \(h\) is \(b\cdot h\).
- A triangle takes up half of the area of a parallelogram with the same base and height. We can therefore express the area \(A\) of a triangle as: \(A=\frac{1}{2}\cdot b\cdot h\)
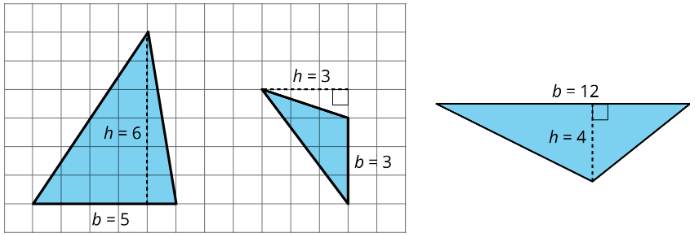
- The area of Triangle A is 15 square units because \(\frac{1}{2}\cdot 5\cdot 6=15\).
- The area of Triangle B is 4.5 square units because \(\frac{1}{2}\cdot 3\cdot 3=4.5\).
- The area of Triangle C is 24 square units because \(\frac{1}{2}\cdot 12\cdot 4=24\).
In each case, one side of the triangle is the base but neither of the other sides is the height. This is because the angle between them is not a right angle.
In right triangles, however, the two sides that are perpendicular can be a base and a height.
The area of this triangle is 18 square units whether we use 4 units or 9 units for the base.
Glossary Entries
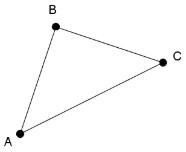
Definition: Opposite Vertex
For each side of a triangle, there is one vertex that is not on that side. This is the opposite vertex.
For example, point \(A\) is the opposite vertex to side \(BC\).
Practice
Exercise \(\PageIndex{4}\)
Select all drawings in which a corresponding height \(h\) for a given base \(b\) is correctly identified.
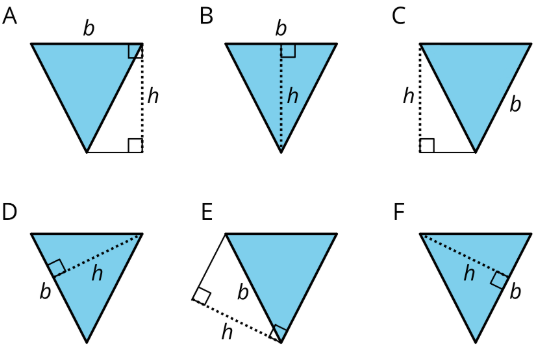
- A
- B
- C
- D
- E
- F
Exercise \(\PageIndex{5}\)
For each triangle, a base and its corresponding height are labeled.
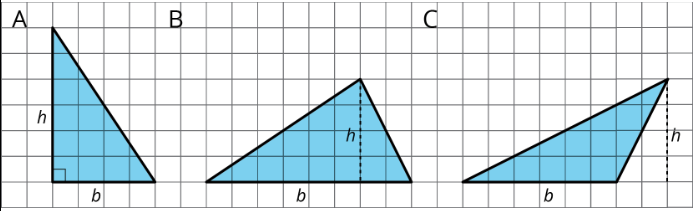
- Find the area of each triangle.
- How is the area related to the base and its corresponding height?
Exercise \(\PageIndex{6}\)
Here is a right triangle. Name a corresponding height for each base.
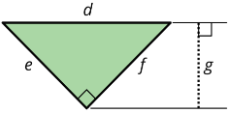
- Side \(d\)
- Side \(e\)
- Side \(f\)
Exercise \(\PageIndex{7}\)
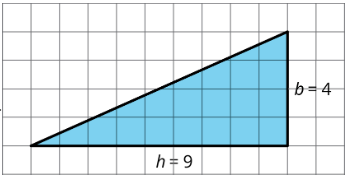
Find the area of the shaded triangle. Show your reasoning.
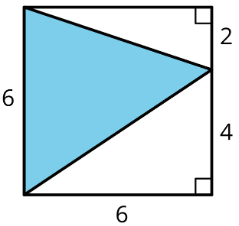
(From Unit 1.3.2)
Exercise \(\PageIndex{8}\)
Andre drew a line connecting two opposite corners of a parallelogram. Select all true statements about the triangles created by the line Andre drew.
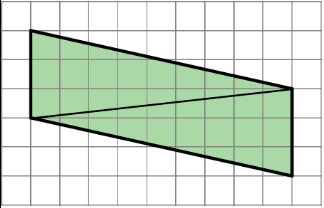
- Each triangle has two sides that are 3 units long.
- Each triangle has a side that is the same length as the diagonal line.
- Each triangle has one side that is 3 units long.
- When one triangle is placed on top of the other and their sides are aligned, we will see that one triangle is larger than the other.
- The two triangles have the same area as each other.
(From Unit 1.3.1)
Exercise \(\PageIndex{9}\)
Here is an octagon. (Note: The diagonal sides of the octagon are not 4 inches long.)
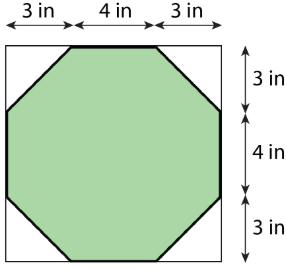
- While estimating the area of the octagon, Lin reasoned that it must be less than 100 square inches. Do you agree? Explain your reasoning.
- Find the exact area of the octagon. Show your reasoning.
(From Unit 1.1.3)


