5.1: Polyhedra
- Page ID
- 39646
Lesson
Let's investigate polyhedra.
Exercise \(\PageIndex{1}\): What are Polyhedra?
Here are pictures that represent polyhedra:
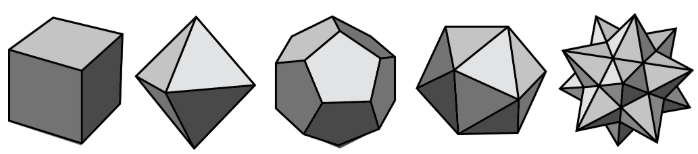
Here are pictures that do not represent polyhedra:
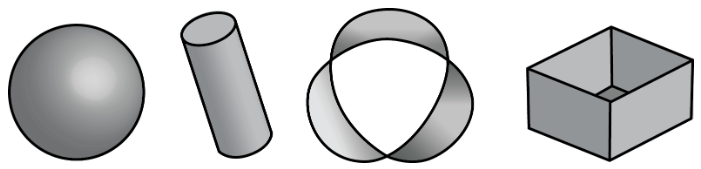
- Your teacher will give you some figures or objects. Sort them into polyhedra and non-polyhedra.
- What features helped you distinguish the polyhedra from the other figures?
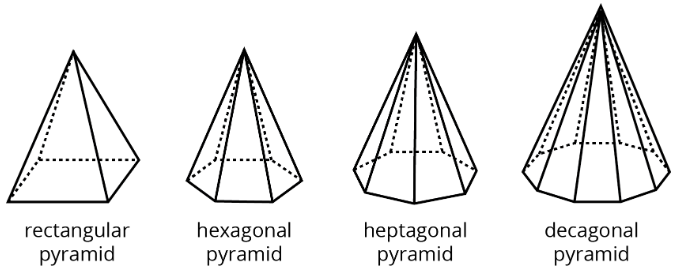
Exercise \(\PageIndex{2}\): Prisms and Pyramids
- Here are some polyhedra called prisms.
Here are some polyhedra called pyramids.
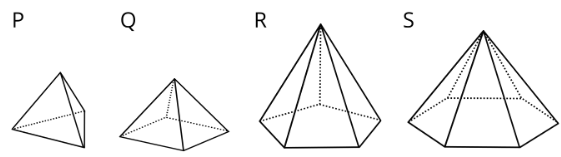
- Look at the prisms. What are their characteristics or features?
- Look at the pyramids. What are their characteristics or features?
- Which of these nets can be folded into Pyramid P? Select all that apply.
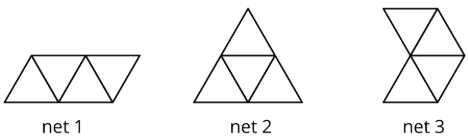
- Your teacher will give your group a set of polygons and assign a polyhedron.
- Decide which polygons are needed to compose your assigned polyhedron. List the polygons and how many of each are needed.
- Arrange the cut-outs into a net that, if taped and folded, can be assembled into the polyhedron. Sketch the net. If possible, find more than one way to arrange the polygons (show a different net for the same polyhedron).
Are you ready for more?
What is the smallest number of faces a polyhedron can possibly have? Explain how you know.
Exercise \(\PageIndex{3}\): Assembling Polyhedra
- Your teacher will give you the net of a polyhedron. Cut out the net, and fold it along the edges to assemble a polyhedron. Tape or glue the flaps so that there are no unjoined edges.
- How many vertices, edges, and faces are in your polyhedron?
Summary
A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only one other face along a complete edge. The ends of the edges meet at points that are called vertices.
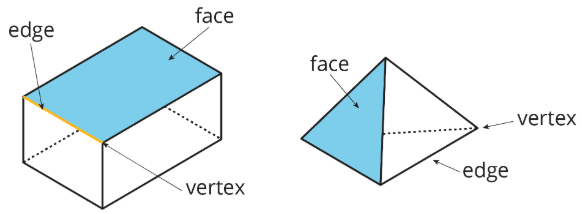
A polyhedron always encloses a three-dimensional region.
The plural of polyhedron is polyhedra. Here are some drawings of polyhedra:
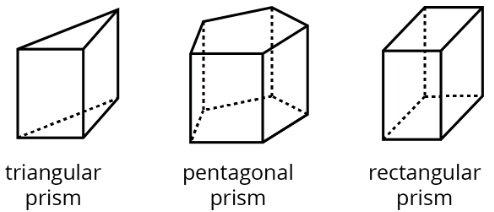
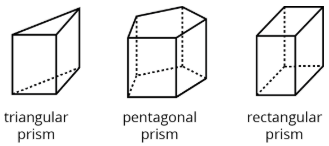
A prism is a type of polyhedron with two identical faces that are parallel to each other and that are called bases. The bases are connected by a set of rectangles (or sometimes parallelograms).
A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a “pentagonal prism.”
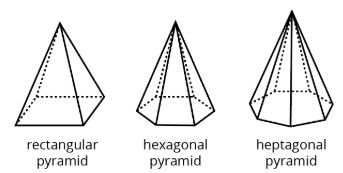
A pyramid is a type of polyhedron that has one special face called the base. All of the other faces are triangles that all meet at a single vertex.
A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a “pentagonal pyramid.”
A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron.
A cube has 6 square faces, so its net is composed of six squares, as shown here.
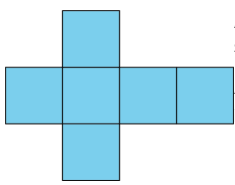
A net can be cut out and folded to make a model of the polyhedron.
In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.
It takes practice to visualize the final polyhedron by just looking at a net.
Glossary Entries
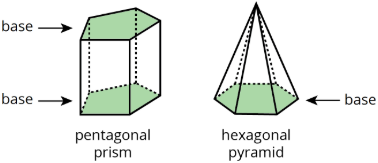
Definition: Base (of a Prism or Pyramid)
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
Definition: Face
Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.
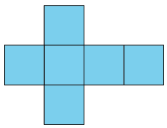
Definition: Net
A net is a two-dimensional figure that can be folded to make a polyhedron.
Here is a net for a cube.
Definition: Polyhedron
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.
Here are some drawings of polyhedra.
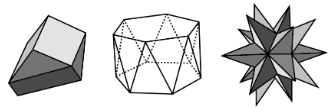
Definition: Prism
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.
Definition: Pyramid
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
Definition: Surface Area
The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.
For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is \(6\cdot 9\), or 54 cm2.
Practice
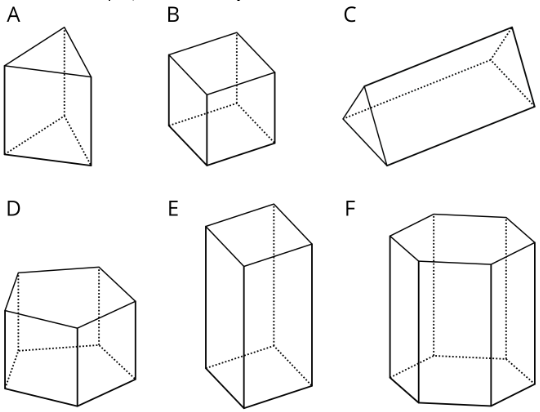
Exercise \(\PageIndex{4}\)
Select all the polyhedra.
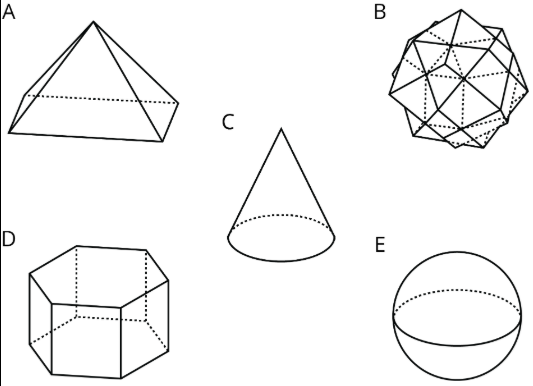
- A
- B
- C
- D
- E
Exercise \(\PageIndex{5}\)
- Is this polyhedron a prism, a pyramid, or neither? Explain how you know.
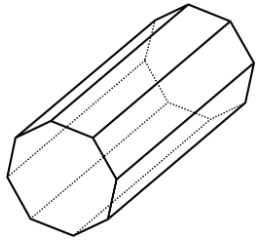
- How many faces, edges, and vertices does it have?
Exercise \(\PageIndex{6}\)
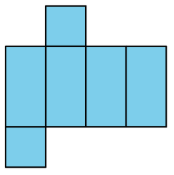
Tyler said this net cannot be a net for a square prism because not all the faces are squares.
Do you agree with Tyler? Explain your reasoning.
Exercise \(\PageIndex{7}\)
Explain why each of these triangles has an area of 9 square units.
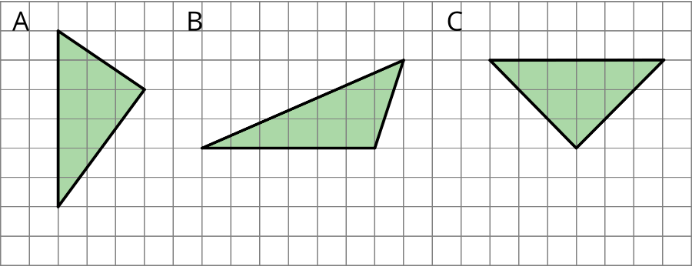
(From Unit 1.3.2)
Exercise \(\PageIndex{8}\)
- A parallelogram has a base of 12 meters and a height of 1.5 meters. What is its area?
- A triangle has a base of 16 inches and a height of \(\frac{1}{8}\) inches. What is its area?
- A parallelogram has an area of 28 square feet and a height of 4 feet. What is its base?
- A triangle has an area of 32 square millimeters and a base of 8 millimeters. What is its height?
(From Unit 1.3.3)
Exercise \(\PageIndex{9}\)
Find the area of the shaded region. Show or explain your reasoning.
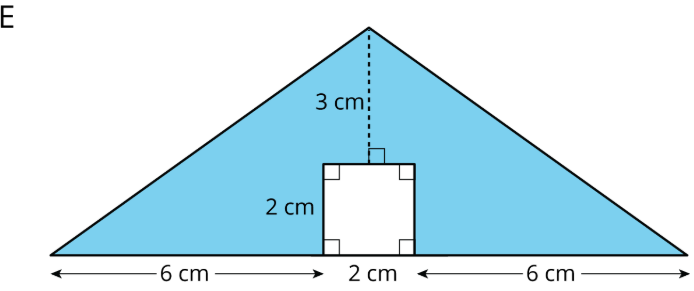
(From Unit 1.1.3)


