32.4: The Distributive Property, Part 1

Lesson

Let's use the distributive property to make calculating easier.

Exercise \(\PageIndex{1}\): Number Talk: Ways to Multiply

Find each product mentally.

\(5\cdot 102\)

\(5\cdot 98\)

\(5\cdot 999\)

Exercise \(\PageIndex{2}\): Ways to Represent Area of a Rectangle

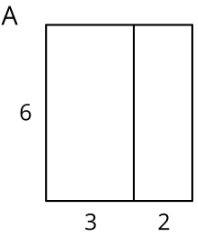
1. Select all the expressions that represent the area of the large, outer rectangle in figure A. Explain your reasoning.
   • \(6+3+2\)
   • \(6\cdot 3+6\cdot 2\)
   • \(6\cdot 3+2\)
   • \(6\cdot 5\)
   • \(6(3+2)\)
   • \(6\cdot 3\cdot 2\)

Figure \(\PageIndex{1}\): One rectangle diagram. Labeled A. Large outer rectangle partitioned into 2 smaller rectangles, vertical side 6. First rectangle bottom side length 3. Second rectangle bottom side length 2.

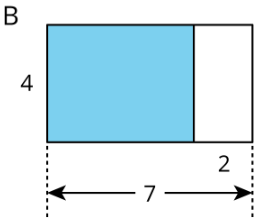
2. Select all the expressions that represent the area of the shaded rectangle on the left side of figure B. Explain your reasoning.
   • \(4\cdot 7+4\cdot 2\)
   • \(4\cdot 7\cdot 2\)
   • \(4\cdot 5\)
   • \(4\cdot 7-4\cdot 2\)
   • \(4(7-2)\)
   • \(4(7+2)\)
   • \(4\cdot 2-4\cdot 7\)

Figure \(\PageIndex{2}\): One rectangle diagram. Labeled B. Large rectangle with bottom side length 7, partitioned into 2 smaller rectangles. First rectangle vertical side 4, bottom side length blank, area shaded blue. Second rectangle vertical side 4, bottom side length 2.

Exercise \(\PageIndex{3}\): Distributive Practice

Complete the table. If you get stuck, skip an entry and come back to it, or consider drawing a diagram of two rectangles that share a side.

Table \(\PageIndex{1}\)

column 1	column 2	column 3	column 4	value
\(5\cdot 98\)	\(5(100-2)\)	\(5\cdot 100-5\cdot 2\)	\(500-10\)	\(490\)
\(33\cdot 12\)	\(33(10+2)\)
		\(3\cdot 10-3\cdot 4\)	\(30-12\)
	\(100(0.04+0.06)\)
		\(8\cdot\frac{1}{2}+8\cdot\frac{1}{4}\)
			\(9+12\)
			\(24-16\)

Are you ready for more?

1. Use the distributive property to write two expressions that equal 360. (There are many correct ways to do this.)
2. Is it possible to write an expression like \(a(b+c)\) that equals 360 where \(a\) is a fraction? Either write such an expression, or explain why it is impossible.
3. Is it possible to write an expression like \(a(b-c)\) that equals 360? Either write such an expression, or explain why it is impossible.
4. How many ways do you think there are to make 360 using the distributive property?

Summary

A term is a single number or variable, or variables and numbers multiplied together. Some examples of terms are 10, \(8x\), \(ab\), and \(7yz\).

When we need to do mental calculations, we often come up with ways to make the calculation easier to do mentally.

Suppose we are grocery shopping and need to know how much it will cost to buy 5 cans of beans at 79 cents a can. We may calculate mentally in this way:

\(\begin{array}{c}{5\cdot 79} \\ {5\cdot 70+5\cdot 9} \\ {350+45} \\ {395}\end{array}\)

In general, when we multiply two terms (or factors), we can break up one of the factors into parts, multiply each part by the other factor, and then add the products. The result will be the same as the product of the two original factors. When we break up one of the factors and multiply the parts we are using the distributive property.

The distributive property also works with subtraction. Here is another way to find \(5\cdot 79\):

\(\begin{array}{c}{5\cdot 79} \\ {5\cdot (80-1)} \\ {400-5} \\ {395}\end{array}\)

Glossary Entries

Definition: Equivalent Expressions

Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.

For example, \(3x+4x\) is equivalent to \(5x+2x\). No matter what value we use for \(x\), these expressions are always equal. When \(x\) is 3, both expressions equal 21. When \(x\) is 10, both expressions equal 70.

Definition: Term

A term is a part of an expression. It can be a single number, a variable, or a number and a variable that are multiplied together. For example, the expression \(5x+18\) has two terms. The first term is \(5x\) and the second term is 18.

Practice

Exercise \(\PageIndex{4}\)

Select all the expressions that represent the area of the large, outer rectangle.

Figure \(\PageIndex{3}\): Area diagram. A large rectangle is partitioned vertically into two smaller rectangles. First rectangle, vertical side 5, bottom side length 2. Second rectangle, vertical side 5, bottom side length 4.

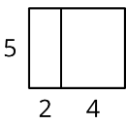
1. \(5(2+4)\)
2. \(5\cdot 2+4\)
3. \(5\cdot 2+5\cdot 4\)
4. \(5\cdot 2\cdot 4\)
5. \(5+2+4\)
6. \(5\cdot 6\)

Exercise \(\PageIndex{5}\)

Draw and label diagrams that show these two methods for calculating \(19\cdot 50\).

• First find \(10\cdot 50\) and then add \(9\cdot 50\).
• First find \(20\cdot 50\) and then take away \(50\).

Exercise \(\PageIndex{6}\)

Complete each calculation using the distributive property.

\(98\cdot 24(100-2)\cdot 24\ldots\)

\(21\cdot 15(20+1)\cdot 15\ldots\)

\(0.51\cdot 40(0.5+0.01)\cdot 40\ldots\)

Exercise \(\PageIndex{7}\)

A group of 8 friends go to the movies. A bag of popcorn costs $2.99. How much will it cost to get one bag of popcorn for each friend? Explain how you can calculate this amount mentally.

Exercise \(\PageIndex{8}\)

1. On graph paper, draw diagrams of \(a+a+a+a\) and \(4a\) when \(a\) is 1, 2, and 3. What do you notice?
2. Do \(a+a+a+a\) and \(4a\) have the same value for any value of \(a\)? Explain how you know.

(From Unit 6.2.3)

Exercise \(\PageIndex{9}\)

120% of \(x\) is equal to 78.

1. Write an equation that shows the relationship of 120%, \(x\), and 78.
2. Use your equation to find \(x\). Show your reasoning.

(From Unit 6.2.2)

Exercise \(\PageIndex{10}\)

Kiran’s aunt is 17 years older than Kiran.

1. How old will Kiran’s aunt be when Kiran is:
   15 years old?
   30 years old?
   \(x\) years old?
2. How old will Kiran be when his aunt is 60 years old?

(From Unit 6.2.1)