32.5: The Distributive Property, Part 2

Lesson

Let's use rectangles to understand the distributive property with variables.

Exercise \(\PageIndex{1}\): Possible Areas

1. A rectangle has a width of 4 units and a length of \(m\) units. Write an expression for the area of this rectangle.
2. What is the area of the rectangle if \(m\) is:
   3 units?
   2.2 units?
   \(\frac{1}{5}\) unit?
3. Could the area of this rectangle be 11 square units? Why or why not?

Exercise \(\PageIndex{2}\): Partitioned Rectangles When Lengths are Unknown

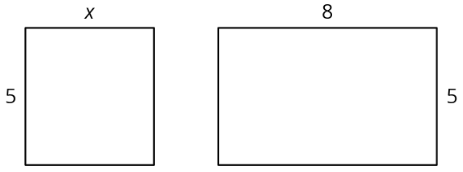
1. Here are two rectangles. The length and width of one rectangle are 8 and 5. The width of the other rectangle is 5, but its length is unknown so we labeled it \(x\).
   Write an expression for the sum of the areas of the two rectangles.

Figure \(\PageIndex{1}\)

2. The two rectangles can be composed into one larger rectangle as shown.
   What are the width and length of the new, large rectangle?

Figure \(\PageIndex{2}\)

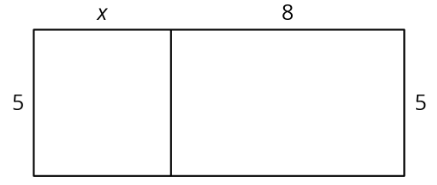
3. Write an expression for the total area of the large rectangle as the product of its width and its length.

Exercise \(\PageIndex{3}\): Areas of Partitioned Rectangles

For each rectangle, write expressions for the length and width and two expressions for the total area. Record them in the table. Check your expressions in each row with your group and discuss any disagreements.

Figure \(\PageIndex{3}\): Six different sized rectangles labeled A, B, C, D, E, and F. Rectangle A is partitioned by a vertical line segment into two smaller rectangles. The vertical side is labeled 3 and the top horizontal side lengths are labeled a and 5. Rectangle B is partitioned by a vertical line segment into two smaller rectangles. The vertical side is labeled one third and the top horizontal side lengths are labeled 6 and x. Rectangle C is partitioned by 2 vertical line segments into three equally sized rectangles. The vertical side is labeled r and the top horizontal side lengths are each labeled 1. Rectangle D is partitioned by 3 vertical line segments into 4 equally sized rectangles. The vertical side is labeled 6, and the top horizontal side lengths are each labeled 4. Rectangle E is partitioned by a vertical line segment into two smaller rectangles. The vertical side is labeled m and the top horizontal side lengths are labeled 6 and 8. Rectangle F is partitioned by a vertical line segment into two smaller rectangles. The vertical side is labeled 5 and the top horizontal side lengths are labeled 3 x and 8.

Table \(\PageIndex{1}\)

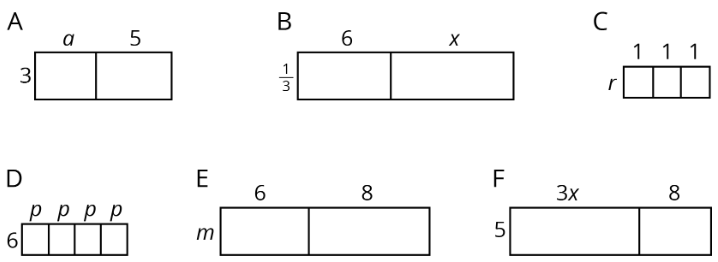
rectangle	width	length	area as a product of width times length	area as a sum of the areas of the smaller rectangles
\(A\)
\(B\)
\(C\)
\(D\)
\(E\)
\(F\)

Are you ready for more?

Here is an area diagram of a rectangle.

Figure \(\PageIndex{4}\): Area diagram. A large rectangle is partitioned vertically and horizontally into four smaller rectangles. Starting with the top left rectangle and moving clockwise, vertical side w, top side y, area A. Top right rectangle, top side length z, area 24. Bottom right rectangle, area 72. Bottom left rectangle, vertical side x, area 18.

1. Find the lengths \(w, x, y,\) and \(z\), and the area \(A\). All values are whole numbers.
2. Can you find another set of lengths that will work? How many possibilities are there?

Summary

Here is a rectangle composed of two smaller rectangles A and B.

Figure \(\PageIndex{5}\): A rectangle is partitioned by a vertical line segment creating two smaller rectangles, A and B. Rectangle A has a vertical side length of 3 and horizontal side length of 2. Rectangle B has a horizontal side length of x.

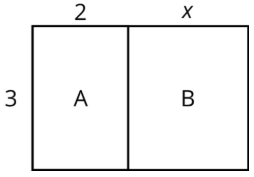
Based on the drawing, we can make several observations about the area of the rectangle:

• One side length of the large rectangle is 3 and the other is \(2+x\), so its area is \(3(2+x)\).
• Since the large rectangle can be decomposed into two smaller rectangles, A and B, with no overlap, the area of the large rectangle is also the sum of the areas of rectangles A and B: \(3(2)+3(x)\) or \(6+3x\).
• Since both expressions represent the area of the large rectangle, they are equivalent to each other. \(3(2+x)\) is equivalent to \(6+3x\).

We can see that multiplying 3 by the sum \(2+x\) is equivalent to multiplying 3 by 2 and then 3 by \(x\) and adding the two products. This relationship is an example of the distributive property.

\(3(2+x)=3\cdot 2+3\cdot x\)

Glossary Entries

Definition: Equivalent Expressions

Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.

For example, \(3x+4x\) is equivalent to \(5x+2x\). No matter what value we use for \(x\), these expressions are always equal. When \(x\) is 3, both expressions equal 21. When \(x\) is 10, both expressions equal 70.

Definition: Term

A term is a part of an expression. It can be a single number, a variable, or a number and a variable that are multiplied together. For example, the expression \(5x+18\) has two terms. The first term is \(5x\) and the second term is 18.

Practice

Exercise \(\PageIndex{4}\)

Here is a rectangle.

Figure \(\PageIndex{6}\): Area diagram. A rectangle partitioned vertically into 3 smaller rectangles. First rectangle, vertical side, a, bottom side 2. Second rectangle, vertical side, a, bottom side, 3. Third rectangle, vertical side, a, bottom side, 4.

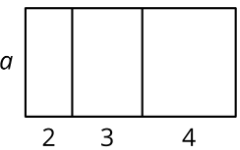
1. Explain why the area of the large rectangle is \(2a+3a+4a\).
2. Explain why the area of the large rectangle is \((2+3+4)a\).

Exercise \(\PageIndex{5}\)

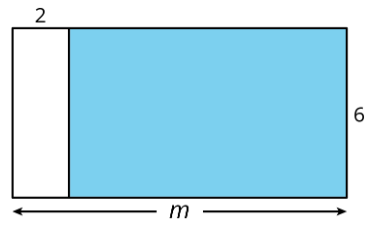
Is the area of the shaded rectangle \(6(2-m)\) or \(6(m-2)\)?

Explain how you know.

Figure \(\PageIndex{7}\): Area diagram of two attached rectangles one with a shaded area. The height of the rectangle is 6 and has a total width of m. Smaller attached rectangle shares the height of 6 and has a width of 2.

Exercise \(\PageIndex{6}\)

Choose the expressions that do not represent the total area of the rectangle. Select all that apply.

Figure \(\PageIndex{8}\)

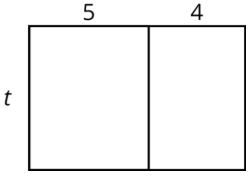
1. \(5t+4t\)
2. \(t+5+4\)
3. \(9t\)
4. \(4\cdot 5\cdot t\)
5. \(t(5+4)\)

Exercise \(\PageIndex{7}\)

Evaluate each expression mentally.

1. \(35\cdot 91-35\cdot 89\)
2. \(22\cdot 87 +22\cdot 13\)
3. \(\frac{9}{11}\cdot\frac{7}{10}-\frac{9}{11}\cdot\frac{3}{10}\)

(From Unit 6.2.4)

Exercise \(\PageIndex{8}\)

Select all the expressions that are equivalent to \(4b\).

1. \(b+b+b+b\)
2. \(b+4\)
3. \(2b+2b\)
4. \(b\cdot b\cdot b\cdot b\)
5. \(b\div\frac{1}{4}\)

(From Unit 6.2.3)

Exercise \(\PageIndex{9}\)

Solve each equation. Show your reasoning.

\(111=14a\)

\(13.65=b+4.88\)

\(c+\frac{1}{3}=5\frac{1}{8}\)

\(\frac{2}{5}d=\frac{17}{4}\)

\(5.16=4e\)

(From Unit 6.1.4)

Exercise \(\PageIndex{10}\)

Andre ran \(5\frac{1}{2}\) laps of a track in 8 minutes at a constant speed. It took Andre \(x\) minutes to run each lap. Select all the equations that represent this situation.

1. \(\left(5\frac{1}{2}\right)x=8\)
2. \(5\frac{1}{2}+x=8\)
3. \(5\frac{1}{2}-x=8\)
4. \(5\frac{1}{2}\div x=8\)
5. \(x=8\div\left(5\frac{1}{2}\right)\)
6. \(x=\left(5\frac{1}{2}\right)\div 8\)

(From Unit 6.1.2)