33.4: Equivalent Exponential Expressions

Lesson

Let's investigate expressions with variables and exponents.

Exercise \(\PageIndex{1}\): Up or Down?

Find the values of \(3^{x}\) and \(\left(\frac{1}{3}\right)^{x}\) for different values of \(x\). What patterns do you notice?

Table \(\PageIndex{1}\)

\(x\)	\(3^{x}\)	\(\left(\frac{1}{3}\right)^{x}\)
\(1\)
\(2\)
\(3\)
\(4\)

Exercise \(\PageIndex{2}\): What's the Value?

Evaluate each expression for the given value of \(x\).

1. \(3x^{2}\) when \(x\) is \(10\)
2. \(3x^{2}\) when \(x\) is \(\frac{1}{9}\)
3. \(\frac{x^{3}}{4}\) when \(x\) is \(4\)
4. \(\frac{x^{3}}{4}\) when \(x\) is \(\frac{1}{2}\)
5. \(9+x^{7}\) when \(x\) is \(1\)
6. \(9+x^{7}\) when \(x\) is \(\frac{1}{2}\)

Exercise \(\PageIndex{3}\): Exponent Experimentation

Find a solution to each equation in the list. (Numbers in the list may be a solution to more than one equation, and not all numbers in the list will be used.)

1. \(64=x^{2}\)
2. \(64=x^{3}\)
3. \(2^{x}=32\)
4. \(x=\left(\frac{2}{5}\right)^{3}\)
5. \(\frac{16}{9}=x^{2}\)
6. \(2\cdot 2^{5}=2^{x}\)
7. \(2x=2^{4}\)
8. \(4^{3}=8^{x}\)

List:

\(\frac{8}{125}\quad \frac{6}{15}\quad\frac{5}{8}\quad\frac{8}{9}\quad 1\frac{4}{3}\quad 2\quad 3\quad 4\quad 5\quad 6\quad 8\)

Are you ready for more?

This fractal is called a Sierpinski Tetrahedron. A tetrahedron is a polyhedron that has four faces. (The plural of tetrahedron is tetrahedra.)

The small tetrahedra form four medium-sized tetrahedra: blue, red, yellow, and green. The medium-sized tetrahedra form one large tetrahedron.

Figure \(\PageIndex{1}\): A large tetrahedron is formed by four medium-sized tetrahedra of different colors: blue, red, yellow, green. Each medium-sized tetrahedron is formed by four small tetrahedra.

1. How many small faces does this fractal have? Be sure to include faces you can’t see. Try to find a way to figure this out so that you don’t have to count every face.
2. How many small tetrahedra are in the bottom layer, touching the table?
3. To make an even bigger version of this fractal, you could take four fractals like the one pictured and put them together. Explain where you would attach the fractals to make a bigger tetrahedron.
4. How many small faces would this bigger fractal have? How many small tetrahedra would be in the bottom layer?
5. What other patterns can you find?

Summary

In this lesson, we saw expressions that used the letter \(x\) as a variable. We evaluated these expressions for different values of \(x\).

• To evaluate the expression \(2x^{3}\) when \(x\) is \(5\), we replace the letter \(x\) with \(5\) to get \(2\cdot 5^{3}\). This is equal to \(2\cdot 125\) or just \(250\). So the value of \(2x^{3}\) is \(250\) when \(x\) is \(5\).
• To evaluate \(\frac{x^{2}}{8}\) when \(x\) is \(4\), we replace the letter \(x\) with \(4\) to get \(\frac{4^{2}}{8}=\frac{16}{8}\), which equals \(2\). So \(\frac{x^{2}}{8}\) has a value of \(2\) when \(x\) is \(4\).

We also saw equations with the variable \(x\) and had to decide what value of \(x\) would make the equation true.

• Suppose we have an equation \(10\cdot 3^{x}=90\) and a list of possible solutions: \(1, 2, 3, 9, 11\). The only value of \(x\) that makes the equation true is \(2\) because \(10\cdot 3^{2}=10\cdot 3\cdot 3\), which equals \(90\). So \(2\) is the solution to the equation.

Practice

Exercise \(\PageIndex{4}\)

Evaluate each expression if \(x=3\).

1. \(2^{x}\)
2. \(x^{2}\)
3. \(1^{x}\)
4. \(x^{1}\)
5. \(\left(\frac{1}{2}\right)^{x}\)

Exercise \(\PageIndex{5}\)

Evaluate each expression for the given value of each variable.

1. \(2+x^{3}\), \(x\) is \(3\)
2. \(x^{2}\), \(x\) is \(\frac{1}{2}\)
3. \(3x^{2}+y\), \(x\) is \(5\) \(y\) is \(3\)
4. \(10y+x^{2}\), \(x\) is \(6\) \(y\) is \(4\)

Exercise \(\PageIndex{6}\)

Decide if the expressions have the same value. If not, determine which expression has the larger value.

1. \(2^{3}\) and \(3^{2}\)
2. \(1^{31}\) and \(31^{1}\)
3. \(4^{2}\) and \(2^{4}\)
4. \(\left(\frac{1}{2}\right)^{3}\) and \(\left(\frac{1}{3}\right)^{2}\)

Exercise \(\PageIndex{7}\)

Match each equation to its solution.

1. \(7+x^{2}=16\)
2. \(5-x^{2}=1\)
3. \(2\cdot 2^{3}=2^{x}\)
4. \(\frac{3^{4}}{3^{x}}=27\)

1. \(x=1\)
2. \(x=2\)
3. \(x=3\)
4. \(x=4\)

Exercise \(\PageIndex{8}\)

An adult pass at the amusement park costs 1.6 times as much as a child’s pass.

1. How many dollars does an adult pass cost if a child’s pass costs:
   \($5\)?
   \($10\)?
   \(w\) dollars?
2. A child's pass costs $15. How many dollars does an adult pass cost?

(From Unit 6.2.1)

Exercise \(\PageIndex{9}\)

Jada reads 5 pages every 20 minutes. At this rate, how many pages can she read in 1 hour?

• Use a double number line to find the answer.

Figure \(\PageIndex{2}\): Double number line, 4 evenly spaced tick marks. Top line, pages read. Beginning at first tick mark, labels: 0, 5, box, box. Bottom line, time minutes. Beginning at first tick mark, labeled 0, 20, 40, 60.

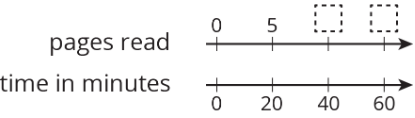
• Use a table to find the answer.

Table \(\PageIndex{2}\)

pages read	time in minutes
\(5\)	\(20\)

Which strategy do you think is better, and why?

(From Unit 2.4.4)