2.4: The Product and Quotient Rules
- Page ID
- 4160
The previous section showed that, in some ways, derivatives behave nicely. The Constant Multiple and Sum/Difference Rules established that the derivative of \(f(x) = 5x^2+\sin x \) was not complicated. We neglected computing the derivative of things like \(g(x) = 5x^2\sin x\) and \(h(x) = \frac{5x^2}{\sin x}\) on purpose; their derivatives are not as straightforward. (If you had to guess what their respective derivatives are, you would probably guess wrong.) For these, we need the Product and Quotient Rules, respectively, which are defined in this section.
We begin with the Product Rule.
Theorem 14: Product Rule
Let \(f\) and \(g\) be differentiable functions on an open interval \(I\). Then \(fg\) is a differentiable function on \(I\), and \[\frac{d}{dx}\Big(f(x)g(x)\Big) = f(x)g^\prime(x) + f^\prime(x)g(x).\]
Important: \(\frac{d}{dx}\Big(f(x)g(x)\Big) \neq f^\prime(x)g^\prime(x)\)! While this answer is simpler than the Product Rule, it is wrong.
We practice using this new rule in an example, followed by an example that demonstrates why this theorem is true.
Example 49: Using the Product Rule
Use the Product Rule to compute the derivative of \(y=5x^2\sin x\). Evaluate the derivative at \(x=\pi/2\).
Solution
To make our use of the Product Rule explicit, let's set \(f(x) = 5x^2\) and \(g(x) = \sin x\). We easily compute/recall that \(f^\prime(x) = 10x\) and \(g^\prime (x) = \cos x\). Employing the rule, we have \[\frac{d}{dx}\Big(5x^2\sin x\Big) = 5x^2\cos x + 10x\sin x.\]
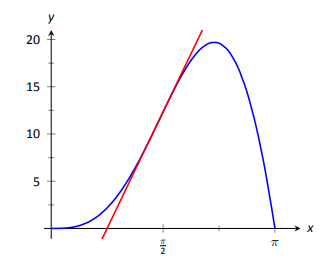
At \(x=\pi/2\), we have \[y^\prime (\pi/2) = 5\left(\frac{\pi}{2}\right)^2\cos \left(\frac{\pi}2\right) + 10\frac{\pi}2 \sin\left(\frac{\pi}{2}\right) = 5\pi.\]We graph \(y\) and its tangent line at \(x=\pi/2\), which has a slope of \(5\pi\), in Figure 2.15. While this does not prove that the Product Rule is the correct way to handle derivatives of products, it helps validate its truth.
We now investigate why the Product Rule is true.
Example 50: A proof of the Product Rule
Use the definition of the derivative to prove Theorem 14.
Solution
By the limit definition, we have
\[\frac{d}{dx}\Big(f(x)g(x)\Big) =\lim_{h\to0} \frac{f(x+h)g(x+h)-f(x)g(x)}{h}.\]
We now do something a bit unexpected; add 0 to the numerator (so that nothing is changed) in the form of \(-f(x+h)g(x)+f(x+h)g(x)\), then do some regrouping as shown.
\[\begin{align*}\frac{d}{dx}\Big(f(x)g(x)\Big) &=\lim_{h\to0} \frac{f(x+h)g(x+h)-f(x)g(x)}{h} \quad \text{(now add 0 to the numerator)}\\ &= \lim_{h\to0} \frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h} \quad \text{(regroup)} \\ &= \lim_{h\to0} \frac{\Big(f(x+h)g(x+h)-f(x+h)g(x)\Big)+\Big(f(x+h)g(x)-f(x)g(x)\Big)}{h}\\ &= \lim_{h\to0} \frac{f(x+h)g(x+h)-f(x+h)g(x)}{h}+\lim_{h\to0}\frac{f(x+h)g(x)-f(x)g(x)}{h}\quad\text{(factor)}\\ &=\lim_{h\to0} f(x+h)\frac{g(x+h)-g(x)}{h}+\lim_{h\to0}\frac{f(x+h)-f(x)}{h}g(x)\quad \text{(apply limits)}\\ &=f(x)g^\prime(x) + f^\prime(x)g(x) \end{align*}\]
It is often true that we can recognize that a theorem is true through its proof yet somehow doubt its applicability to real problems. In the following example, we compute the derivative of a product of functions in two ways to verify that the Product Rule is indeed "right.''
Example 51: Exploring alternate derivative methods
Let \(y = (x^2+3x+1)(2x^2-3x+1)\). Find \(y^prime\) two ways: first, by expanding the given product and then taking the derivative, and second, by applying the Product Rule. Verify that both methods give the same answer.
Solution
We first expand the expression for \(y\); a little algebra shows that \(y = 2x^4+3x^3-6x^2+1\). It is easy to compute \(y^\prime\); \[y^\prime = 8x^3+9x^2-12x.\]
Now apply the Product Rule.
\[\begin{align*}y^\prime &= (x^2+3x+1)(4x-3)+(2x+3)(2x^2-3x+1) \\ &= \big(4x^3+9x^2-5x-3\big) + \big(4x^3-7x+3\big)\\ & = 8x^3+9x^2-12x. \end{align*}\]
The uninformed usually assume that "the derivative of the product is the product of the derivatives.'' Thus we are tempted to say that \(y^\prime = (2x+3)(4x-3) = 8x^2+6x-9\). Obviously this is not correct.
Example 52: Using the Product Rule with a product of these three functions
Let \(y = x^3\ln x\cos x\). Find \(y^\prime\).
Solution
We have a product of three functions while the Product Rule only specifies how to handle a product of two functions. Our method of handling this problem is to simply group the latter two functions together, and consider \(y = x^3\big(\ln x\cos x\big)\). Following the Product Rule, we have
\[\begin{align*} y^\prime &= (x^3)\big(\ln x\cos x\big)' + 3x^2\big(\ln x\cos x\big) \\ &\text{To evaluate \(\big(\ln x\cos x\big)^\prime\), we apply the Product Rule again:}\\ &= (x^3)\big(\ln x(-\sin x) + \frac1x\cos x\big)+ 3x^2\big(\ln x\cos x\big)\\ &= x^3\ln x(-\sin x) + x^3\frac1x\cos x+ 3x^2\ln x\cos x \end{align*}\]
Recognize the pattern in our answer above: when applying the Product Rule to a product of three functions, there are three terms added together in the final derivative. Each terms contains only one derivative of one of the original functions, and each function's derivative shows up in only one term. It is straightforward to extend this pattern to finding the derivative of a product of 4 or more functions.
We consider one more example before discussing another derivative rule.
Example 53: Using the Product Rule
Find the derivatives of the following functions.
- \(f(x) = x\ln x\)
- \(g(x) = x\ln x - x\).
Solution:
Recalling that the derivative of \(\ln x\) is \(1/x\), we use the Product Rule to find our answers.
- \( \frac{d}{dx}\Big(x\ln x\Big) = x\cdot 1/x + 1\cdot \ln x = 1+\ln x\).
- Using the result from above, we compute \[ \frac{d}{dx}\Big(x\ln x-x\Big) = 1+\ln x-1 = \ln x.\]
This seems significant; if the natural log function \(\ln x\) is an important function (it is), it seems worthwhile to know a function whose derivative is \(\ln x\). We have found one. (We leave it to the reader to find another; a correct answer will be very similar to this one.)
We have learned how to compute the derivatives of sums, differences, and products of functions. We now learn how to find the derivative of a quotient of functions.
Theorem 15: Quotient Rule
Let \(f\) and \(g\) be functions defined on an open interval \(I\), where \(g(x) \neq 0\) on \(I\). Then \(f/g\) is differentiable on \(I\), and
\[\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{g(x)f^\prime(x) - f(x)g^\prime(x)}{g(x)^2}.\]
The Quotient Rule is not hard to use, although it might be a bit tricky to remember. A useful mnemonic works as follows. Consider a fraction's numerator and denominator as "HI'' and "LO'', respectively. Then \[\frac{d}{dx}\left(\frac{\text{HI}}{\text{LO}}\right) = \frac{\text{LO}\cdot \text{dHI} - \text{HI} \cdot \text{dLO}}{\text{LOLO}},\]read "low dee high minus high dee low, over low low.'' Said fast, that phrase can roll off the tongue, making it easy to memorize. The "dee high'' and "dee low'' parts refer to the derivatives of the numerator and denominator, respectively.
Let's practice using the Quotient Rule.
Example 54: Using the Quotient Rule
Let \( f(x) = \frac{5x^2}{\sin x}\). Find \(f^\prime(x)\).
Solution
Directly applying the Quotient Rule gives:
\[\begin{align*} \frac{d}{dx}\left(\frac{5x^2}{\sin x}\right) &= \frac{\sin x\cdot 10x - 5x^2\cdot \cos x}{\sin^2x} \\ &= \frac{10x\sin x - 5x^2\cos x}{\sin^2 x}. \end{align*}\]
The Quotient Rule allows us to fill in holes in our understanding of derivatives of the common trigonometric functions. We start with finding the derivative of the tangent function.
Example 55
Using the Quotient Rule to find \(\frac{d}{dx}\big(\tan x\big)\).
Find the derivative of \(y=\tan x\).
Solution
At first, one might feel unequipped to answer this question. But recall that \(\tan x = \sin x/\cos x\), so we can apply the Quotient Rule.
\[\begin{align*} \frac{d}{dx}\Big(\tan x\Big) &= \frac{d}{dx}\left(\frac{\sin x}{\cos x}\right) \\ &= \frac{\cos x \cos x - \sin x (-\sin x)}{\cos^2 x} \\ &= \frac{\cos^2x+\sin^2x}{\cos^2x}\\ &= \frac{1}{\cos^2x} \\ &= \sec ^2 x. \end{align*}\]
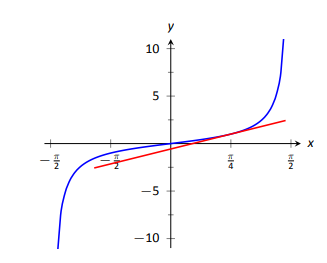
This is a beautiful result. To confirm its truth, we can find the equation of the tangent line to \(y=\tan x\) at \(x=\pi/4\). The slope is \(\sec^2(\pi/4) = 2\); \(y=\tan x\), along with its tangent line, is graphed in Figure 2.16.
We include this result in the following theorem about the derivatives of the trigonometric functions. Recall we found the derivative of \(y=\sin x\) in Example 38 and stated the derivative of the cosine function in Theorem 12. The derivatives of the cotangent, cosecant and secant functions can all be computed directly using Theorem 12 and the Quotient Rule.
Theorem 16: Derivatives of Trigonometric Functions
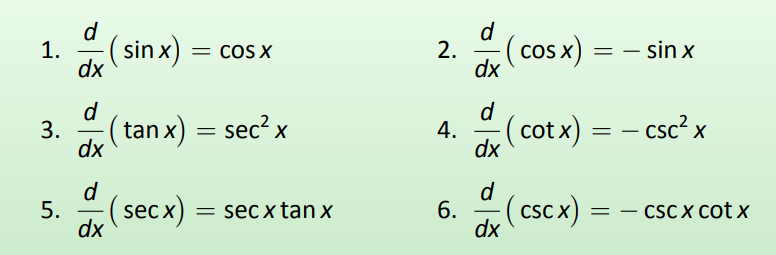
To remember the above, it may be helpful to keep in mind that the derivatives of the trigonometric functions that start with "c'' have a minus sign in them.
Example 56: Exploring alternative derivative methods
In Example 54 the derivative of \( f(x) = \frac{5x^2}{\sin x}\) was found using the Quotient Rule. Rewriting \(f\) as \(f(x) = 5x^2\csc x\), find \(f^\prime\) using Theorem 16 and verify the two answers are the same.}
Solution
We found in Example 54 that the \( f^\prime(x) = \frac{10x\sin x - 5x^2\cos x}{\sin^2 x}\). We now find \(f^\prime\) using the Product Rule, considering \(f\) as \(f(x) = 5x^2\csc x\).
\[\begin{align*} f^\prime(x) &= \frac{d}{dx}\Big(5x^2\csc x\Big) \\ &= 5x^2(-\csc x\cot x) + 10x\csc x \quad \text{(now rewrite trig functions)}\\ &= 5x^2\cdot \frac{-1}{\sin x}\cdot \frac{\cos x}{\sin x} + \frac{10x}{\sin x}\\ &= \frac{-5x^2\cos x}{\sin ^2x}+\frac{10x}{\sin x}\quad \text{(get common denominator)}\\ &= \frac{10x\sin x - 5x^2\cos x}{\sin^2x} \end{align*}\]
Finding \(f^\prime\) using either method returned the same result. At first, the answers looked different, but some algebra verified they are the same. In general, there is not one final form that we seek; the immediate result from the Product Rule is fine. Work to "simplify'' your results into a form that is most readable and useful to you.
The Quotient Rule gives other useful results, as show in the next example.
Example 57: Using the Quotient Rule to expand the Power Rule
Find the derivatives of the following functions.
- \(f(x) = \frac{1}{x}\)
- \( f(x)= \frac{1}{x^n}\), where \(n>0\) is an integer.
Solution
We employ the Quotient Rule.
- \( f^\prime(x) = \frac{x\cdot 0 - 1\cdot 1}{x^2} = -\frac{1}{x^2}\).
- \(f^\prime(x) = \frac{x^n\cdot 0 - 1\cdot nx^{n-1}}{(x^n)^2} = -\frac{nx^{n-1}}{x^{2n}} = -\frac{n}{x^{n+1}}.\)
The derivative of \( y=\frac{1}{x^n}\) turned out to be rather nice. It gets better. Consider:
\[\begin{align*} \frac{d}{dx}\left(\frac{1}{x^n}\right) &= \frac{d}{dx}\Big(x^{-n}\Big)\quad \text{(apply result from Example 57)}\\ &= -\frac{n}{x^{n+1}}\text{(rewrite algebraically)} \\ &= -nx^{-(n+1)} \\ &= -nx^{-n-1}. \end{align*}\]
This is reminiscent of the Power Rule: multiply by the power, then subtract 1 from the power. We now add to our previous Power Rule, which had the restriction of \(n>0\).
Theorem 17: Power Rule with Integer Exponents
Let \(f(x) = x^n\), where \(n\neq 0\) is an integer. Then \[f^\prime(x) = n\cdot x^{n-1}.\]
Taking the derivative of many functions is relatively straightforward. It is clear (with practice) what rules apply and in what order they should be applied. Other functions present multiple paths; different rules may be applied depending on how the function is treated. One of the beautiful things about calculus is that there is not "the'' right way; each path, when applied correctly, leads to the same result, the derivative. We demonstrate this concept in an example.
Example 58: Exploring alternate derivative methods
Let \(f(x) = \frac{x^2-3x+1}{x}\). Find \(f^\prime(x)\) in each of the following ways:
- By applying the Quotient Rule,
- by viewing \(f\) as \(f(x) = \big(x^2-3x+1\big)\cdot x^{-1}\) and applying the Product and Power Rules, and
- by "simplifying\primeskip'' first through division.
Verify that all three methods give the same result.
Solution
- Applying the Quotient Rule gives: \[ f^\prime(x) = \frac{x\cdot\big(2x-3\big)-\big(x^2-3x+1\big)\cdot 1}{x^2} = \frac{x^2-1}{x^2} = 1-\frac{1}{x^2}.\]
- By rewriting \(f\), we can apply the Product and Power Rules as follows:\[\begin{align*} f^\prime(x) &= \big(x^2-3x+1\big)\cdot (-1)x^{-2} + \big(2x-3\big)\cdot x^{-1} \\ &= -\frac{x^2-3x+1}{x^2}+\frac{2x-3}{x} \\ &= -\frac{x^2-3x+1}{x^2}+\frac{2x^2-3x}{x^2}\\ &= \frac{x^2-1}{x^2} = 1-\frac{1}{x^2}, \end{align*}\]the same result as above.
- As \(x\neq 0\), we can divide through by \(x\) first, giving \( f(x) = x-3+\frac{1}x\). Now apply the Power Rule. \[f^\prime(x) = 1-\frac{1}{x^2},\]the same result as before.
Example 58 demonstrates three methods of finding \(f^\prime\). One is hard pressed to argue for a "best method'' as all three gave the same result without too much difficulty, although it is clear that using the Product Rule required more steps. Ultimately, the important principle to take away from this is: reduce the answer to a form that seems "simple'' and easy to interpret. In that example, we saw different expressions for \(f^\prime\), including:
\[1-\frac{1}{x^2} = \frac{x\cdot\big(2x-3\big)-\big(x^2-3x+1\big)\cdot 1}{x^2} = \big(x^2-3x+1\big)\cdot (-1)x^{-2} + \big(2x-3\big)\cdot x^{-1}.\]
They are equal; they are all correct; only the first is "clear.'' Work to make answers clear.
In the next section we continue to learn rules that allow us to more easily compute derivatives than using the limit definition directly. We have to memorize the derivatives of a certain set of functions, such as "the derivative of \(\sin x\) is \(\cos x\).'' The Sum/Difference, Constant Multiple, Power, Product and Quotient Rules show us how to find the derivatives of certain combinations of these functions. The next section shows how to find the derivatives when we compose these functions together.


