2.5: Adjectives for Functions
- Page ID
- 459
As we have defined it in Section 1.3, a function is a very general object. At this point, it is useful to introduce a collection of adjectives to describe certain kinds of functions; these adjectives name useful properties that functions may have. Consider the graphs of the functions in Figure 2.5.1. It would clearly be useful to have words to help us describe the distinct features of each of them. We will point out and define a few adjectives (there are many more) for the functions pictured here. For the sake of the discussion, we will assume that the graphs do not exhibit any unusual behavior off-stage (i.e., outside the view of the graphs).
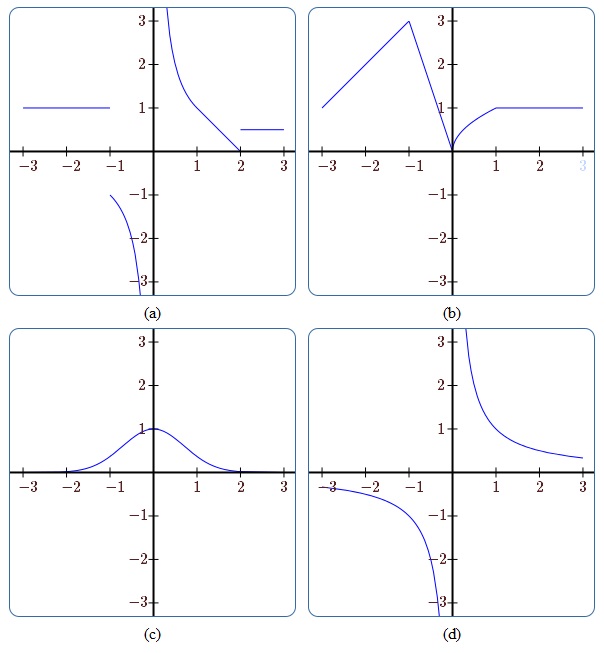
Functions. Each graph in Figure 2.5.1 certainly represents a function---since each passes the vertical line test. In other words, as you sweep a vertical line across the graph of each function, the line never intersects the graph more than once. If it did, then the graph would not represent a function.
Bounded. The graph in (c) appears to approach zero as \(x\) goes to both positive and negative infinity. It also never exceeds the value \(1\) or drops below the value \(0\). Because the graph never increases or decreases without bound, we say that the function represented by the graph in (c) is a bounded function.
Definition 2.5.1: Bounded Functions
A function \(f\) is bounded if there is a number \(M\) such that \(|f(x)| < M\) for every \(x\) in the domain of \(f\).
For the function in (c), one such choice for \(M\) would be \(10\). However, the smallest (optimal) choice would be \(M=1\). In either case, simply finding an \(M\) is enough to establish boundedness. No such \(M\) exists for the hyperbola in (d) and hence we can say that it is unbounded.
Continuity. The graphs shown in (b) and (c) both represent continuous functions. Geometrically, this is because there are no jumps in the graphs. That is, if you pick a point on the graph and approach it from the left and right, the values of the function approach the value of the function at that point. For example, we can see that this is not true for function values near \(x=-1\) on the graph in (a) which is not continuous at that location.
Definition 2.5.2: Continuous at a Point
A function \(f\) is continuous at a point \(a\) if \( \lim_{x\to a} f(x) = f(a)\).
Definition 2.5.3: Continuous
A function \(f\) is continuous if it is continuous at every point in its domain.
Strangely, we can also say that (d) is continuous even though there is a vertical asymptote. A careful reading of the definition of continuous reveals the phrase "at every point in its domain.'' Because the location of the asymptote, \(x=0\), is not in the domain of the function, and because the rest of the function is well-behaved, we can say that (d) is continuous.
Differentiability. Now that we have introduced the derivative of a function at a point, we can begin to use the adjective differentiable. We can see that the tangent line is well-defined at every point on the graph in (c). Therefore, we can say that (c) is a differentiable function.
Definition 2.5.4: Differentiable at a Point
A function \(f\) is differentiable at point \(a\) if \(f'(a)\) exists.
Definition 2.5.5: Differentiable Function
A function \(f\) is differentiable if is differentiable at every point (excluding endpoints and isolated points in the domain of \(f\)) in the domain of \(f\).
Take note that, for technical reasons not discussed here, both of these definitions exclude endpoints and isolated points in the domain from consideration. We now have a collection of adjectives to describe the very rich and complex set of objects known as functions. We close with a useful theorem about continuous functions:
Theorem 2.5.6: Intermediate Value Theorem
If \(f\) is continuous on the interval \([a,b]\) and \(d\) is between \(f(a)\) and \(f(b)\), then there is a number \(c\) in \([a,b]\) such that \(f(c)=d\).
This is most frequently used when \(d=0\).
, \(f\) is continuous. Since \(f(0)=-2\) and \(f(1)=3\), and \(0\) is between \(-2\) and \(3\), there is a \(c\in[0,1]\) such that \(f(c)=0\).
This example also points the way to a simple method for approximating roots.
If we compute \(f(0.1)\), \(f(0.2)\), and so on, we find that \(f(0.6) < 0\) and \(f(0.7)>0\), so by the Intermediate Value Theorem, \(f\) has a root between \(0.6\) and \(0.7\). Repeating the process with \(f(0.61)\), \(f(0.62)\), and so on, we find that \(f(0.61) < 0\) and \(f(0.62)>0\), so \(f\) has a root between \(0.61\) and \(0.62\), and the root is \(0.6\) rounded to one decimal place.


