4.4: The Derivative of sin x - II
- Page ID
- 479
Now we can complete the calculation of the derivative of the sine:
\[\eqalign{ {d\over dx}\sin x &= \lim_{\Delta x\to0} {\sin(x+\Delta x)-\sin x \over \Delta x}\cr& =\lim_{\Delta x\to0} \sin x{\cos \Delta x - 1\over \Delta x}+\cos x{\sin\Delta x\over \Delta x}\cr& =\sin x \cdot 0 + \cos x \cdot 1 = \cos x.\cr }\]
The derivative of a function measures the slope or steepness of the function; if we examine the graphs of the sine and cosine side by side, it should be that the latter appears to accurately describe the slope of the former, and indeed this is true:
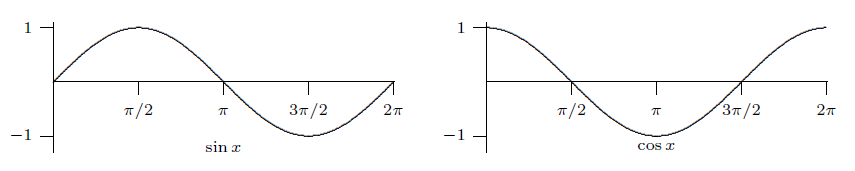
\[{d\over dx}\sin(x^2) = \cos(x^2)\cdot 2x = 2x\cos(x^2).\]
\[\eqalign{ {d\over dx}\sin^2(x^3-5x)&={d\over dx}(\sin(x^3-5x))^2\cr& =2(\sin(x^3-5x))^1\cos(x^3-5x)(3x^2-5)\cr& =2(3x^2-5)\cos(x^3-5x)\sin(x^3-5x).\cr }\]
Contributors
Integrated by Justin Marshall.


