12.5: Equations of Lines and Planes in Space
- Page ID
- 2590
- Write the vector, parametric, and symmetric equations of a line through a given point in a given direction, and a line through two given points.
- Find the distance from a point to a given line.
- Write the vector and scalar equations of a plane through a given point with a given normal.
- Find the distance from a point to a given plane.
- Find the angle between two planes.
By now, we are familiar with writing equations that describe a line in two dimensions. To write an equation for a line, we must know two points on the line, or we must know the direction of the line and at least one point through which the line passes. In two dimensions, we use the concept of slope to describe the orientation, or direction, of a line. In three dimensions, we describe the direction of a line using a vector parallel to the line. In this section, we examine how to use equations to describe lines and planes in space.
Equations for a Line in Space
Let’s first explore what it means for two vectors to be parallel. Recall that parallel vectors must have the same or opposite directions. If two nonzero vectors, \( \vecs{u}\) and \( \vecs{v}\), are parallel, we claim there must be a scalar, \( k\), such that \( \vecs{u}=k\vecs{v}\). If \( \vecs{u}\) and \( \vecs{v}\) have the same direction, simply choose
\[ k=\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
If \( \vecs{u}\) and \( \vecs{v}\) have opposite directions, choose
\[ k=−\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
Note that the converse holds as well. If \( \vecs{u}=k \vecs{v}\) for some scalar \( k\), then either \( \vecs{u}\) and \(\vecs{ v}\) have the same direction \( (k>0)\) or opposite directions \( (k<0)\), so \( \vecs{u}\) and \( \vecs{v}\) are parallel. Therefore, two nonzero vectors \( \vecs{u}\) and \(\vecs{ v}\) are parallel if and only if \( \vecs{u}=k\vecs{v}\) for some scalar \( k\). By convention, the zero vector \( \vecs{0}\) is considered to be parallel to all vectors.
Figure \(\PageIndex{1}\): Vector \(\vecs{v}\) is the direction vector for \( \vecd{PQ}\).
As in two dimensions, we can describe a line in space using a point on the line and the direction of the line, or a parallel vector, which we call the direction vector (Figure \(\PageIndex{1}\)). Let \( L\) be a line in space passing through point \( P(x_0,y_0,z_0)\). Let \( \vecs{v}=⟨a,b,c⟩\) be a vector parallel to \( L\). Then, for any point on line \( Q(x,y,z)\), we know that \( \vecd{PQ}\) is parallel to \( \vecs{v}\). Thus, as we just discussed, there is a scalar, \( t\), such that \( \vecd{PQ}=t\vecs{v}\), which gives
\[ \begin{align} \vecd{PQ} &=t\vecs{v} \nonumber \\[4pt]
⟨x−x_0,y−y_0,z−z_0⟩ &=t⟨a,b,c⟩ \nonumber \\[4pt]
⟨x−x_0,y−y_0,z−z_0⟩ &=⟨ta,tb,tc⟩. \label{eq1} \end{align} \]
Using vector operations, we can rewrite Equation \ref{eq1}
\[ \begin{align*} ⟨x−x_0,y−y_0,z−z_0⟩ &=⟨ta,tb,tc⟩ \\[4pt]
⟨x,y,z⟩−⟨x_0,y_0,z_0⟩ &=t⟨a,b,c⟩ \\[4pt]
\underbrace{⟨x,y,z⟩}_{\vecs{r}} &=\underbrace{⟨x_0,y_0,z_0⟩}_{\vecs{r}_o}+t\underbrace{⟨a,b,c⟩}_{\vecs{v}}.\end{align*}\]
Setting \( \vecs{r}=⟨x,y,z⟩\) and \( \vecs{r}_0=⟨x_0,y_0,z_0⟩\), we now have the vector equation of a line:
\[ \vecs{r}=\vecs{r}_0+t\vecs{v}. \label{vector} \]
Equating components, Equation \ref{vector} shows that the following equations are simultaneously true: \( x−x_0=ta, y−y_0=tb,\) and \( z−z_0=tc.\) If we solve each of these equations for the component variables \( x,y,\) and \( z\), we get a set of equations in which each variable is defined in terms of the parameter \(t\) and that, together, describe the line. This set of three equations forms a set of parametric equations of a line:
\[ x=x_0+ta \nonumber \]
\[ y=y_0+tb \nonumber \]
\[ z=z_0+tc.\nonumber \]
If we solve each of the equations for \( t\) assuming \( a,b\), and \( c\) are nonzero, we get a different description of the same line:
\[ \begin{align*} \dfrac{x−x_0}{a} =t \\[4pt] \dfrac{y−y_0}{b} =t \\[4pt] \dfrac{z−z_0}{c} =t.\end{align*}\]
Because each expression equals \(t\), they all have the same value. We can set them equal to each other to create symmetric equations of a line:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
We summarize the results in the following theorem.
A line \( L\) parallel to vector \( \vecs{v}=⟨a,b,c⟩\) and passing through point \( P(x_0,y_0,z_0)\) can be described by the following parametric equations:
\[ x=x_0+ta, y=y_0+tb, \nonumber \]
and
\[ z=z_0+tc. \nonumber \]
If the constants \( a,b,\) and \( c\) are all nonzero, then \( L\) can be described by the symmetric equation of the line:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
The parametric equations of a line are not unique. Using a different parallel vector or a different point on the line leads to a different, equivalent representation. Each set of parametric equations leads to a related set of symmetric equations, so it follows that a symmetric equation of a line is not unique either.
Find parametric and symmetric equations of the line passing through points \( (1,4,−2)\) and \( (−3,5,0).\)
Solution
First, identify a vector parallel to the line:
\[ \vecs v=⟨−3−1,5−4,0−(−2)⟩=⟨−4,1,2⟩. \nonumber \]
Use either of the given points on the line to complete the parametric equations:
\[\begin{align*} x =1−4t \\[4pt] y =4+t, \end{align*}\]
and
\[ z=−2+2t. \nonumber \]
Solve each equation for \( t\) to create the symmetric equation of the line:
\[ \dfrac{x−1}{−4}=y−4=\dfrac{z+2}{2}. \nonumber \]
Find parametric and symmetric equations of the line passing through points \( (1,−3,2)\) and \( (5,−2,8).\)
- Hint:
-
Start by finding a vector parallel to the line.
- Answer
-
Possible set of parametric equations: \( x=1+4t,\; y=−3+t,\; z=2+6t;\) related set of symmetric equations: \[ \dfrac{x−1}{4}=y+3=\dfrac{z−2}{6} \nonumber \]
Sometimes we don’t want the equation of a whole line, just a line segment. In this case, we limit the values of our parameter \( t\). For example, let \( P(x_0,y_0,z_0)\) and \( Q(x_1,y_1,z_1)\) be points on a line, and let \( \vecs p=⟨x_0,y_0,z_0⟩\) and \( \vecs q=⟨x_1,y_1,z_1⟩\) be the associated position vectors. In addition, let \(\vecs r=⟨x,y,z⟩\). We want to find a vector equation for the line segment between \( P\) and \( Q\). Using \( P\) as our known point on the line, and \( \vecd{PQ}=⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\) as the direction vector equation, Equation \ref{vector} gives
\[\vecs{r}=\vecs{p}+t(\vecd{PQ}). \label{eq10} \]
Equation \ref{eq10} can be expanded using properties of vectors:
\[ \begin{align*} \vecs{r} &=\vecs{p}+t(\vecd{PQ}) \\[4pt]
&=⟨x_0,y_0,z_0⟩+t⟨x_1−x_0,y_1−y_0,z_1−z_0⟩ \\[4pt]
&=⟨x_0,y_0,z_0⟩+t(⟨x_1,y_1,z_1⟩−⟨x_0,y_0,z_0⟩) \\[4pt]
&=⟨x_0,y_0,z_0⟩+t⟨x_1,y_1,z_1⟩−t⟨x_0,y_0,z_0⟩ \\[4pt]
&=(1−t)⟨x_0,y_0,z_0⟩+t⟨x_1,y_1,z_1⟩ \\[4pt]
&=(1−t)\vecs{p}+t\vecs{q}. \end{align*}\]
Thus, the vector equation of the line passing through \( P\) and \( Q\) is
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q}. \nonumber \]
Remember that we did not want the equation of the whole line, just the line segment between \( P\) and \( Q\). Notice that when \( t=0\), we have \(\vecs{r}=\vecs{p}\), and when \( t=1\), we have \( \vecs r=\vecs q\). Therefore, the vector equation of the line segment between \( P\) and \( Q\) is
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q},0≤t≤1. \nonumber \]
Going back to Equation \ref{vector}, we can also find parametric equations for this line segment. We have
\[ \begin{align*} \vecs{r} &=\vecs{p}+t(\vecd{PQ}) \\[4pt]
⟨x,y,z⟩ &=⟨x_0,y_0,z_0⟩+t⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\\[4pt]
&=⟨x_0+t(x_1−x_0),y_0+t(y_1−y_0),z_0+t(z_1−z_0)⟩. \end{align*}\]
Then, the parametric equations are
\[ \begin{align} x &=x_0+t(x_1−x_0) \nonumber\\[4pt] y &=y_0+t(y_1−y_0) \label{para}\\[4pt] z &=z_0+t(z_1−z_0), \quad 0≤t≤1. \nonumber\end{align} \]
Find parametric equations of the line segment between the points \( P(2,1,4)\) and \( Q(3,−1,3).\)
Solution
Start with the parametric equations for a line (Equations \ref{para}) and work with each component separately:
\[ \begin{align*} x &=x_0+t(x_1−x_0)\\[4pt] &=2+t(3−2)\\[4pt] &=2+t, \end{align*}\]
\[ \begin{align*} y &=y_0+t(y_1−y_0)\\[4pt] &=1+t(−1−1)\\[4pt] &=1−2t, \end{align*}\]
and
\[ \begin{align*} z &=z_0+t(z_1−z_0)\\[4pt] &=4+t(3−4)\\[4pt] &=4−t. \end{align*}\]
Therefore, the parametric equations for the line segment are
\[ \begin{align*} x &=2+t\\[4pt] y &=1−2t\\[4pt] z &=4−t,\quad 0≤t≤1.\end{align*}\]
Find parametric equations of the line segment between points \( P(−1,3,6)\) and \( Q(−8,2,4)\).
- Answer
-
\( x=−1−7t,\; y=3−t,\; z=6−2t, \quad 0≤t≤1 \)
Distance between a Point and a Line
We already know how to calculate the distance between two points in space. We now expand this definition to describe the distance between a point and a line in space. Several real-world contexts exist when it is important to be able to calculate these distances. When building a home, for example, builders must consider “setback” requirements, when structures or fixtures have to be a certain distance from the property line. Air travel offers another example. Airlines are concerned about the distances between populated areas and proposed flight paths.
Let \( L\) be a line in the plane and let \( M\) be any point not on the line. Then, we define distance \( d\) from \( M\) to \( L\) as the length of line segment \( \overline{MP}\), where \( P\) is a point on \( L\) such that \( \overline{MP}\) is perpendicular to \( L\) (Figure \(\PageIndex{2}\)).
When we’re looking for the distance between a line and a point in space, Figure \(\PageIndex{2}\) still applies. We still define the distance as the length of the perpendicular line segment connecting the point to the line. In space, however, there is no clear way to know which point on the line creates such a perpendicular line segment, so we select an arbitrary point on the line and use properties of vectors to calculate the distance. Therefore, let \( P\) be an arbitrary point on line \( L\) and let \(\vecs{v}\) be a direction vector for \( L\) (Figure \(\PageIndex{3}\)).
Vectors \( \vecd{PM}\) and \(\vecs{v}\) form two sides of a parallelogram with area \( ‖\vecd{PM}×\vecs{v}‖\). Using a formula from geometry, the area of this parallelogram can also be calculated as the product of its base and height:
\[‖\vecd{PM}×\vecs{v}‖=‖\vecs v‖d. \nonumber \]
We can use this formula to find a general formula for the distance between a line in space and any point not on the line.
Let \( L\) be a line in space passing through point \( P\) with direction vector \(\vecs{v}\). If \( M\) is any point not on \( L\), then the distance from \( M\) to \( L\) is
\[d=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖}. \nonumber \]
Find the distance between the point \( M=(1,1,3)\) and line \( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)
Solution:
From the symmetric equations of the line, we know that vector \( \vecs{v}=⟨4,2,1⟩\) is a direction vector for the line. Setting the symmetric equations of the line equal to zero, we see that point \( P(3,−1,3)\) lies on the line. Then,
\[\begin{align*} \vecd{PM} =⟨1−3,1−(−1),3−3⟩\\[4pt] =⟨−2,2,0⟩. \end{align*}\]
To calculate the distance, we need to find \( \vecd{PM}×\vecs v:\)
\[\begin{align*} \vecd{PM}×\vecs{v} &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−2 & 2 & 0\\4 & 2 & 1\end{vmatrix} \\[4pt] &=(2−0)\mathbf{\hat i}−(−2−0)\mathbf{\hat j}+(−4−8)\mathbf{\hat k} \\[4pt]
&=2\mathbf{\hat i}+2\mathbf{\hat j}−12\mathbf{\hat k}. \end{align*}\]
Therefore, the distance between the point and the line is (Figure \(\PageIndex{4}\))
\[\begin{align*} d &=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖} \\[4pt]
&=\dfrac{\sqrt{2^2+2^2+12^2}}{\sqrt{4^2+2^2+1^2}}\\[4pt]
&=\dfrac{2\sqrt{38}}{\sqrt{21}}\\[4pt]
&=\dfrac{2\sqrt{798}}{21} \,\text{units} \end{align*}\]

Find the distance between point \( (0,3,6)\) and the line with parametric equations \( x=1−t,\; y=1+2t,\; z=5+3t.\)
- Hint
-
Find a vector with initial point \( (0,3,6)\) and a terminal point on the line, and then find a direction vector for the line.
- Answer
-
\( \sqrt{\dfrac{10}{7}} = \dfrac{\sqrt{70}}{7} \,\text{units} \)
Relationships between Lines
Given two lines in the two-dimensional plane, the lines are equal, they are parallel but not equal, or they intersect in a single point. In three dimensions, a fourth case is possible. If two lines in space are not parallel, but do not intersect, then the lines are said to be skew lines (Figure \(\PageIndex{5}\)).
Figure \(\PageIndex{5}\): In three dimensions, it is possible that two lines do not cross, even when they have different directions.
To classify lines as parallel but not equal, equal, intersecting, or skew, we need to know two things: whether the direction vectors are parallel and whether the lines share a point (Figure \(\PageIndex{6}\)).
For each pair of lines, determine whether the lines are equal, parallel but not equal, skew, or intersecting.
a.
- \( L_1:\; x=2s−1, \; y=s−1, \; z=s−4\)
- \( L_2: \; x=t−3, \; y=3t+8, \; z=5−2t\)
b.
- \( L_1: \; x=−y=z\)
- \( L_2:\; \dfrac{x−3}{2}=y=z−2\)
c.
- \( L_1:\; x=6s−1,\; y=−2s,\; z=3s+1\)
- \( L_2:\; \dfrac{x−4}{6}=\dfrac{y+3}{−2}=\dfrac{z−1}{3}\)
Solution
a. Line \( L_1\) has direction vector \( \vecs v_1=⟨2,1,1⟩\); line \( L_2\) has direction vector \( \vecs v_2=⟨1,3,−2⟩\). Because the direction vectors are not parallel vectors, the lines are either intersecting or skew. To determine whether the lines intersect, we see if there is a point, \( (x,y,z)\), that lies on both lines. To find this point, we use the parametric equations to create a system of equalities:
\[ 2s−1=t−3; \nonumber \]
\[ s−1=3t+8; \nonumber \]
\[ s−4=5−2t. \nonumber \]
By the first equation, \( t=2s+2.\) Substituting into the second equation yields
\( s−1=3(2s+2)+8\)
\( s−1=6s+6+8\)
\( 5s=−15\)
\( s=−3.\)
Substitution into the third equation, however, yields a contradiction:
\( s−4=5−2(2s+2)\)
\( s−4=5−4s−4\)
\( 5s=5\)
\( s=1.\)
There is no single point that satisfies the parametric equations for \( L_1\) and \( L_2\) simultaneously. These lines do not intersect, so they are skew (see the following figure).
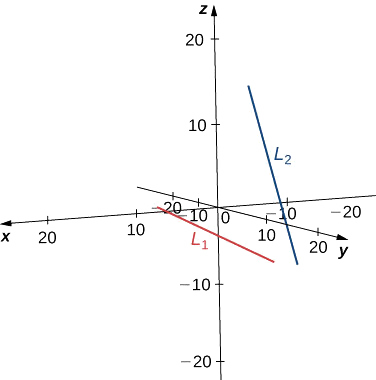
b. Line \( L_1\) has direction vector \( \vecs v_1=⟨1,−1,1⟩\) and passes through the origin, \( (0,0,0)\). Line \( L_2\) has a different direction vector, \( \vecs v_2=⟨2,1,1⟩\), so these lines are not parallel or equal. Let \( r\) represent the parameter for line \( L_1\) and let \(s\) represent the parameter for \( L_2\):
\[\begin{align*} &\text{Line }L_1: & & \text{Line }L_2:\\[4pt] &x = r & & x = 2s + 3\\[4pt] &y = -r & & y = s \\[4pt] &z = r & & z = s + 2 \end{align*}\]
Solve the system of equations to find \( r=1\) and \( s=−1\). If we need to find the point of intersection, we can substitute these parameters into the original equations to get \( (1,−1,1)\) (see the following figure).

c. Lines \( L_1\) and \( L_2\) have equivalent direction vectors: \( \vecs v=⟨6,−2,3⟩.\) These two lines are parallel (see the following figure).

Describe the relationship between the lines with the following parametric equations:
\[ x=1−4t, \; y=3+t, \; z=8−6t \nonumber \]
\[x=2+3s,\; y=2s,\; z=−1−3s. \nonumber \]
- Hint
-
Start by identifying direction vectors for each line. Is one a multiple of the other?
- Answer
-
These lines are skew because their direction vectors are not parallel and there is no point \( (x,y,z)\) that lies on both lines.
Equations for a Plane
We know that a line is determined by two points. In other words, for any two distinct points, there is exactly one line that passes through those points, whether in two dimensions or three. Similarly, given any three points that do not all lie on the same line, there is a unique plane that passes through these points. Just as a line is determined by two points, a plane is determined by three.
This may be the simplest way to characterize a plane, but we can use other descriptions as well. For example, given two distinct, intersecting lines, there is exactly one plane containing both lines. A plane is also determined by a line and any point that does not lie on the line. These characterizations arise naturally from the idea that a plane is determined by three points. Perhaps the most surprising characterization of a plane is actually the most useful.
Imagine a pair of orthogonal vectors that share an initial point. Visualize grabbing one of the vectors and twisting it. As you twist, the other vector spins around and sweeps out a plane. Here, we describe that concept mathematically. Let \(\vecs{n}=⟨a,b,c⟩\) be a vector and \(P=(x_0,y_0,z_0)\) be a point. Then the set of all points \(Q=(x,y,z)\) such that \(\vecd{PQ}\) is orthogonal to \(\vecs{n}\) forms a plane (Figure \(\PageIndex{7}\)). We say that \(\vecs{n}\) is a normal vector, or perpendicular to the plane. Remember, the dot product of orthogonal vectors is zero. This fact generates the vector equation of a plane:
\[\vecs{n}⋅\vecd{PQ}=0. \nonumber \]
Rewriting this equation provides additional ways to describe the plane:
\[ \begin{align*} \vecs{n}⋅\vecd{PQ} &=0 \\[4pt] ⟨a,b,c⟩⋅⟨x−x_0,y−y_0,z−z_0⟩ &=0 \\[4pt] a(x−x_0)+b(y−y_0)+c(z−z_0) &=0. \end{align*}\]
Given a point \(P\) and vector \(\vecs n\), the set of all points \(Q\) satisfying the equation \(\vecs n⋅\vecd{PQ}=0\) forms a plane. The equation
\[\vecs{n}⋅\vecd{PQ}=0 \nonumber \]
is known as the vector equation of a plane.
The scalar equation of a plane (sometimes also called the standard equation of a plane) containing point \(P=(x_0,y_0,z_0)\) with normal vector \(\vec{n}=⟨a,b,c⟩\) is
\[a(x−x_0)+b(y−y_0)+c(z−z_0)=0. \nonumber \]
This equation can be expressed as \(ax+by+cz+d=0,\) where \(d=−ax_0−by_0−cz_0.\) This form of the equation is sometimes called the general form of the equation of a plane.
As described earlier in this section, any three points that do not all lie on the same line determine a plane. Given three such points, we can find an equation for the plane containing these points.
Write an equation for the plane containing points \(P=(1,1,−2), Q=(0,2,1),\) and \(R=(−1,−1,0)\) in both standard and general forms.
Solution
To write an equation for a plane, we must find a normal vector for the plane. We start by identifying two vectors in the plane:
\[ \begin{align*} \vecd{PQ} &=⟨0−1,2−1,1−(−2)⟩\\[4pt] &=⟨−1,1,3⟩ \\[4pt] \vecd{QR} &=⟨−1−0,−1−2,0−1⟩\\[4pt] &=⟨−1,−3,−1⟩.\end{align*}\]
The cross product \(\vecd{PQ}×\vecd{QR}\) is orthogonal to both \(\vecd{PQ}\) and \(\vecd{QR}\), so it is normal to the plane that contains these two vectors:
\[ \begin{align*} \vecs n &=\vecd{PQ}×\vecd{QR} \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−1 & 1 & 3\\−1 & −3 & −1\end{vmatrix} \\[4pt] &=(−1+9)\mathbf{\hat i}−(1+3)\mathbf{\hat j}+(3+1)\mathbf{\hat k} \\[4pt] &= 8\mathbf{\hat i}−4\mathbf{\hat j}+4\mathbf{\hat k}.\end{align*}\]
Thus, \(\vecs n=⟨8,−4,4⟩,\) and we can choose any of the three given points to write an equation of the plane:
\[ \begin{align*} 8(x−1)−4(y−1)+4(z+2) &=0 \\[4pt] 8x−4y+4z+4 &=0. \end{align*}\]
The scalar equations of a plane vary depending on the normal vector and point chosen.
Find an equation of the plane that passes through point \((1,4,3)\) and contains the line given by \(x=\dfrac{y−1}{2}=z+1.\)
Solution
Symmetric equations describe the line that passes through point \((0,1,−1)\) parallel to vector \(\vecs v_1=⟨1,2,1⟩\) (see the following figure). Use this point and the given point, \((1,4,3),\) to identify a second vector parallel to the plane:
\[ \vecs v_2=⟨1−0,4−1,3−(−1)⟩=⟨1,3,4⟩. \nonumber \]
Use the cross product of these vectors to identify a normal vector for the plane:
\[ \begin{align*} \vecs n &=\vecs v_1×\vecs v_2 \nonumber \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\1 & 2 & 1\\1 & 3 & 4\end{vmatrix} \nonumber \\[4pt] &=(8−3)\mathbf{\hat i}−(4−1)\mathbf{\hat j}+(3−2)\mathbf{\hat k} \\[4pt] &=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}. \nonumber\end{align*}\]
The scalar equations for the plane are \(5x−3(y−1)+(z+1)=0\) and \(5x−3y+z+4=0.\)
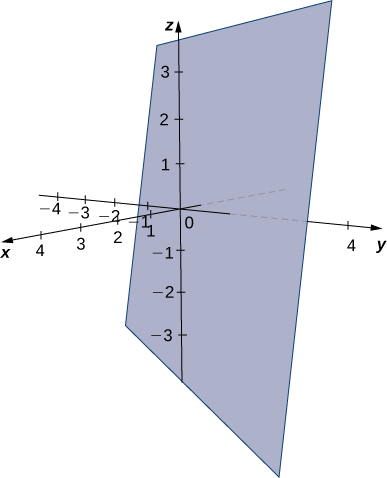
Find an equation of the plane containing the lines \(L_1\) and \(L_2\):
\[ L_1: \; x=−y=z \nonumber \]
\[ L_2:\; \dfrac{x−3}{2}=y=z−2. \nonumber \]
- Hint
-
Hint: The cross product of the lines’ direction vectors gives a normal vector for the plane.
- Answer
-
\[ −2(x−1)+(y+1)+3(z−1)=0 \nonumber \]
or
\[ −2x+y+3z=0 \nonumber \]
Now that we can write an equation for a plane, we can use the equation to find the distance \(d\) between a point \(P\) and the plane. It is defined as the shortest possible distance from \(P\) to a point on the plane.
Just as we find the two-dimensional distance between a point and a line by calculating the length of a line segment perpendicular to the line, we find the three-dimensional distance between a point and a plane by calculating the length of a line segment perpendicular to the plane. Let \(R\) be the point in the plane such that \(\vecd{RP}\) is orthogonal to the plane, and let \(Q\) be an arbitrary point in the plane. Then the projection of vector \(\vecd{QP}\) onto the normal vector describes vector \(\vecd{RP}\), as shown in Figure \(\PageIndex{8}\).
Suppose a plane with normal vector \(\vecs{n}\) passes through point \(Q\). The distance \(d\) from the plane to a point \(P\) not in the plane is given by
\[d=‖\text{proj}_\vecs{n}\,\vecd{QP}‖=∣\text{comp}_\vecs{n}\, \vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs{n}∣}{‖\vecs{n}‖}. \label{distanceplanepoint} \]
Find the distance between point \(P=(3,1,2)\) and the plane given by \(x−2y+z=5\) (see the following figure).
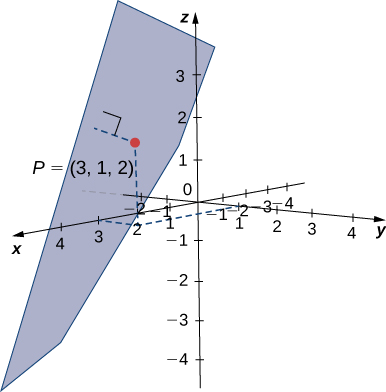
Solution
The coefficients of the plane’s equation provide a normal vector for the plane: \(\vecs{n}=⟨1,−2,1⟩\). To find vector \(\vecd{QP}\), we need a point in the plane. Any point will work, so set \(y=z=0\) to see that point \(Q=(5,0,0)\) lies in the plane. Find the component form of the vector from \(Q\) to \(P\):
\[ \vecd{QP}=⟨3−5,1−0,2−0⟩=⟨−2,1,2⟩. \nonumber \]
Apply the distance formula from Equation \ref{distanceplanepoint}:
\[\begin{align*} d &=\dfrac{\left|\vecd{QP}⋅\vecs n\right|}{‖\vecs n‖} \\[4pt] &=\dfrac{|⟨−2,1,2⟩⋅⟨1,−2,1⟩|}{\sqrt{1^2+(−2)^2+1^2}} \\[4pt] &=\dfrac{|−2−2+2|}{\sqrt{6}} \\[4pt] &=\dfrac{2}{\sqrt{6}} = \dfrac{\sqrt{6}}{3}\,\text{units}. \end{align*}\]
Find the distance between point \(P=(5,−1,0)\) and the plane given by \(4x+2y−z=3\).
- Hint
-
Point \((0,0,−3)\) lies on the plane.
- Answer
-
\[ \dfrac{15}{\sqrt{21}} = \dfrac{5\sqrt{21}}{7}\,\text{units} \nonumber \]
Parallel and Intersecting Planes
We have discussed the various possible relationships between two lines in two dimensions and three dimensions. When we describe the relationship between two planes in space, we have only two possibilities: the two distinct planes are parallel or they intersect. When two planes are parallel, their normal vectors are parallel. When two planes intersect, the intersection is a line (Figure \(\PageIndex{9}\)).
We can use the equations of the two planes to find parametric equations for the line of intersection.
Find parametric and symmetric equations for the line formed by the intersection of the planes given by \(x+y+z=0\) and \(2x−y+z=0\) (see the following figure).
Solution
Note that the two planes have nonparallel normals, so the planes intersect. Further, the origin satisfies each equation, so we know the line of intersection passes through the origin. Add the plane equations so we can eliminate one of the variables, in this case, \(y\):
\(x+y+z=0\)
\(2x−y+z=0\)
________________
\(3x+2z=0\).
This gives us \(x=−\dfrac{2}{3}z.\) We substitute this value into the first equation to express \(y\) in terms of \(z\):
\[ \begin{align*} x+y+z =0 \\[4pt] −\dfrac{2}{3}z+y+z =0 \\[4pt] y+\dfrac{1}{3}z =0 \\[4pt] y =−\dfrac{1}{3}z \end{align*}. \nonumber \]
We now have the first two variables, \(x\) and \(y\), in terms of the third variable, \(z\). Now we define \(z\) in terms of \(t\). To eliminate the need for fractions, we choose to define the parameter \(t\) as \(t=−\dfrac{1}{3}z\). Then, \(z=−3t\). Substituting the parametric representation of \(z\) back into the other two equations, we see that the parametric equations for the line of intersection are \(x=2t, \; y=t, \; z=−3t.\) The symmetric equations for the line are \(\dfrac{x}{2}=y=\dfrac{z}{−3}\).
Find parametric equations for the line formed by the intersection of planes \(x+y−z=3\) and \(3x−y+3z=5.\)
- Hint
-
Add the two equations, then express \(z\) in terms of \(x\). Then, express \(y\) in terms of \(x\).
- Answer
-
\( x=t, \; y=7−3t,\; z=4−2t\)
In addition to finding the equation of the line of intersection between two planes, we may need to find the angle formed by the intersection of two planes. For example, builders constructing a house need to know the angle where different sections of the roof meet to know whether the roof will look good and drain properly. We can use normal vectors to calculate the angle between the two planes. We can do this because the angle between the normal vectors is the same as the angle between the planes. Figure \(\PageIndex{10}\) shows why this is true.
We can find the measure of the angle \(θ\) between two intersecting planes by first finding the cosine of the angle, using the following equation:
\[\cos θ=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖}. \nonumber \]
We can then use the angle to determine whether two planes are parallel or orthogonal or if they intersect at some other angle.
Determine whether each pair of planes is parallel, orthogonal, or neither. If the planes are intersecting, but not orthogonal, find the measure of the angle between them. Give the answer in radians and round to two decimal places.
- \(x+2y−z=8\) and \(2x+4y−2z=10\)
- \(2x−3y+2z=3\) and \(6x+2y−3z=1\)
- \(x+y+z=4\) and \(x−3y+5z=1\)
Solution:
- The normal vectors for these planes are \(\vecs{n}_1=⟨1,2,−1⟩\) and \(\vecs{n}_2=⟨2,4,−2⟩.\) These two vectors are scalar multiples of each other. The normal vectors are parallel, so the planes are parallel.
- The normal vectors for these planes are \(\vecs{n}_1=⟨2,−3,2⟩\) and \(\vecs{n}_2=⟨6,2,−3⟩\). Taking the dot product of these vectors, we have \[\begin{align*} \vecs{n}_1⋅\vecs{n}_2 =⟨2,−3,2⟩⋅⟨6,2,−3⟩\\[4pt] =2(6)−3(2)+2(−3)=0.\end{align*} \nonumber \] The normal vectors are orthogonal, so the corresponding planes are orthogonal as well.
- The normal vectors for these planes are \(\vecs n_1=⟨1,1,1⟩\) and \(\vecs n_2=⟨1,−3,5⟩\): \[\begin{align*} \cos θ &=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖} \\[4pt] &=\dfrac{|⟨1,1,1⟩⋅⟨1,−3,5⟩|}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(−3)^2+5^2}} \\[4pt] &=\dfrac{3}{\sqrt{105}} \end{align*}\]
Then \(\theta =\arccos {\frac{3}{\sqrt{105}}} \approx 1.27\) rad.
Thus the angle between the two planes is about \(1.27\) rad, or approximately \(73°\).
Find the measure of the angle between planes \(x+y−z=3\) and \(3x−y+3z=5.\) Give the answer in radians and round to two decimal places.
- Hint
-
Use the coefficients of the variables in each equation to find a normal vector for each plane.
- Answer
-
\( 1.44\, \text{rad} \)
When we find that two planes are parallel, we may need to find the distance between them. To find this distance, we simply select a point in one of the planes. The distance from this point to the other plane is the distance between the planes.
Previously, we introduced the formula for calculating this distance in Equation \ref{distanceplanepoint}:
\[d=\dfrac{\vecd{QP}⋅\vecs{n}}{‖\vecs{n}‖}, \nonumber \]
where \(Q\) is a point on the plane, \(P\) is a point not on the plane, and \(\vec{n}\) is the normal vector that passes through point \(Q\). Consider the distance from point \((x_0,y_0,z_0)\) to plane \(ax+by+cz+k=0.\) Let \((x_1,y_1,z_1)\) be any point in the plane. Substituting into the formula yields
\[\begin{align*}d =\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}} \\[4pt] =\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}.\end{align*}\]
We state this result formally in the following theorem.
Let \(P(x_0,y_0,z_0)\) be a point. The distance from \(P\) to plane \(ax+by+cz+k=0\) is given by
\[d=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}. \nonumber \]
Find the distance between the two parallel planes given by \(2x+y−z=2\) and \(2x+y−z=8.\)
Solution
Point \((1,0,0)\) lies in the first plane. The desired distance, then, is
\[\begin{align*} d &=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \\[4pt] &= \dfrac{|2(1)+1(0)+(−1)(0)+(−8)|}{\sqrt{2^2+1^2+(−1)^2}} \\[4pt] &= \dfrac{6}{\sqrt{6}}=\sqrt{6} \,\text{units} \end{align*}\]
Find the distance between parallel planes \(5x−2y+z=6\) and \(5x−2y+z=−3\).
- Hint
-
Set \(x=y=0\) to find a point on the first plane.
- Answer
-
\(\dfrac{9}{\sqrt{30}} = \dfrac{3\sqrt{30}}{10}\,\text{units} \)
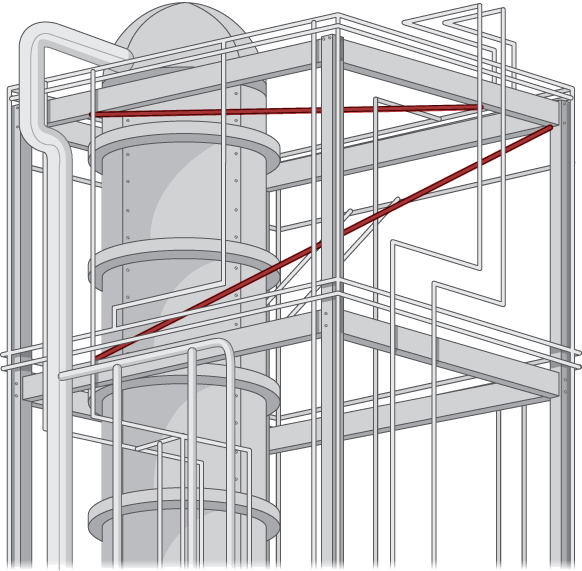
Finding the distance from a point to a line or from a line to a plane seems like a pretty abstract procedure. But, if the lines represent pipes in a chemical plant or tubes in an oil refinery or roads at an intersection of highways, confirming that the distance between them meets specifications can be both important and awkward to measure. One way is to model the two pipes as lines, using the techniques in this chapter, and then calculate the distance between them. The calculation involves forming vectors along the directions of the lines and using both the cross product and the dot product.
The symmetric forms of two lines, \(L_1\) and \(L_2\), are
\[L_1:\dfrac{x−x_1}{a_1}=\dfrac{y−y_1}{b_1}=\dfrac{z−z_1}{c_1} \nonumber \]
\[L_2:\dfrac{x−x_2}{a_2}=\dfrac{y−y_2}{b_2}=\dfrac{z−z_2}{c_2}. \nonumber \]
You are to develop a formula for the distance \(d\) between these two lines, in terms of the values \(a_1,b_1,c_1;a_2,b_2,c_2;x_1,y_1,z_1;\) and \(x_2,y_2,z_2.\) The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length of a vector that is perpendicular to both lines and intersects both lines.
1. First, write down two vectors, \(\vecs{v}_1\) and \(\vecs{v}_2\), that lie along \(L_1\) and \(L_2\), respectively.
2. Find the cross product of these two vectors and call it \(\vecs{N}\). This vector is perpendicular to \(\vecs{v}_1\) and \(\vecs{v}_2\), and hence is perpendicular to both lines.
3. From vector \(\vecs{N}\), form a unit vector \(\vecs{n}\) in the same direction.
4. Use symmetric equations to find a convenient vector \(\vecs{v}_{12}\) that lies between any two points, one on each line. Again, this can be done directly from the symmetric equations.
5. The dot product of two vectors is the magnitude of the projection of one vector onto the other—that is, \(\vecs A⋅\vecs B=‖\vecs{A}‖‖\vecs{B}‖\cos θ,\) where \(θ\) is the angle between the vectors. Using the dot product, find the projection of vector \(\vecs{v}_{12}\) found in step \(4\) onto unit vector \(\vecs{n}\) found in step \(3\). This projection is perpendicular to both lines, and hence its length must be the perpendicular distance d between them. Note that the value of \(d\) may be negative, depending on your choice of vector \(\vecs{v}_{12}\) or the order of the cross product, so use absolute value signs around the numerator.
6. Check that your formula gives the correct distance of \(|−25|/\sqrt{198}≈1.78\) between the following two lines:
\[L_1:\dfrac{x−5}{2}=\dfrac{y−3}{4}=\dfrac{z−1}{3} \nonumber \]
\[L_2:\dfrac{x−6}{3}=\dfrac{y−1}{5}=\dfrac{z}{7}. \nonumber \]
7. Is your general expression valid when the lines are parallel? If not, why not? (Hint: What do you know about the value of the cross product of two parallel vectors? Where would that result show up in your expression for \(d\)?)
8. Demonstrate that your expression for the distance is zero when the lines intersect. Recall that two lines intersect if they are not parallel and they are in the same plane. Hence, consider the direction of \(\vecs{n}\) and \(\vecs{v}_{12}\). What is the result of their dot product?
9. Consider the following application. Engineers at a refinery have determined they need to install support struts between many of the gas pipes to reduce damaging vibrations. To minimize cost, they plan to install these struts at the closest points between adjacent skewed pipes. Because they have detailed schematics of the structure, they are able to determine the correct lengths of the struts needed, and hence manufacture and distribute them to the installation crews without spending valuable time making measurements.
The rectangular frame structure has the dimensions \(4.0×15.0×10.0\,\text{m}\) (height, width, and depth). One sector has a pipe entering the lower corner of the standard frame unit and exiting at the diametrically opposed corner (the one farthest away at the top); call this \(L_1\). A second pipe enters and exits at the two different opposite lower corners; call this \(L_2\) (Figure \(\PageIndex{12}\)).
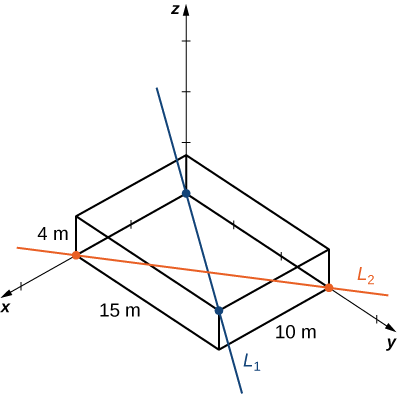
Write down the vectors along the lines representing those pipes, find the cross product between them from which to create the unit vector \(\vecs n\), define a vector that spans two points on each line, and finally determine the minimum distance between the lines. (Take the origin to be at the lower corner of the first pipe.) Similarly, you may also develop the symmetric equations for each line and substitute directly into your formula.
Key Concepts
- In three dimensions, the direction of a line is described by a direction vector. The vector equation of a line with direction vector \(\vecs v=⟨a,b,c⟩\) passing through point \(P=(x_0,y_0,z_0)\) is \(\vecs r=\vecs r_0+t\vecs v\), where \(\vecs r_0=⟨x_0,y_0,z_0⟩\) is the position vector of point \(P\). This equation can be rewritten to form the parametric equations of the line: \(x=x_0+ta,y=y_0+tb\), and \(z=z_0+tc\). The line can also be described with the symmetric equations \(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\).
- Let \(L\) be a line in space passing through point \(P\) with direction vector \(\vecs v\). If \(Q\) is any point not on \(L\), then the distance from \(Q\) to \(L\) is \(d=\dfrac{‖\vecd{PQ}×\vecs v‖}{‖\vecs v‖}.\)
- In three dimensions, two lines may be parallel but not equal, equal, intersecting, or skew.
- Given a point \(P\) and vector \(\vecs n\), the set of all points \(Q\) satisfying equation \(\vecs n⋅\vecd{PQ}=0\) forms a plane. Equation \(\vecs n⋅\vecd{PQ}=0\) is known as the vector equation of a plane.
- The scalar equation of a plane containing point \(P=(x_0,y_0,z_0)\) with normal vector \(\vecs n=⟨a,b,c⟩\) is \(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\). This equation can be expressed as \(ax+by+cz+d=0,\) where \(d=−ax_0−by_0−cz_0.\) This form of the equation is sometimes called the general form of the equation of a plane.
- Suppose a plane with normal vector \(n\) passes through point \(Q\). The distance \(D\) from the plane to point \(P\) not in the plane is given by
\[D=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vec{QP}∣=\dfrac{∣\vec{QP}⋅\vecs n∣}{‖\vecs n‖.} \nonumber \]
- The normal vectors of parallel planes are parallel. When two planes intersect, they form a line.
- The measure of the angle \(θ\) between two intersecting planes can be found using the equation: \(\cos θ=\dfrac{|\vecs{n}_1⋅\vecs n_2|}{‖\vecs n_1‖‖\vecs n_2‖}\), where \(\vecs n_1\) and \(\vecs n_2\) are normal vectors to the planes.
- The distance \(D\) from point \((x_0,y_0,z_0)\) to plane \(ax+by+cz+d=0\) is given by
\[D=\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|} {\sqrt{a^2+b^2+c^2}}=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \nonumber \].
Key Equations
- Vector Equation of a Line
\(\vecs r=\vecs r_0+t\vecs v\)
- Parametric Equations of a Line
\(x=x_0+ta,\; y=y_0+tb,\) and \(z=z_0+tc\)
- Symmetric Equations of a Line
\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\)
- Vector Equation of a Plane
\(\vecs n⋅\vecd{PQ}=0\)
- Scalar Equation of a Plane
\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\)
- Distance between a Plane and a Point
\(d=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs n∣}{‖\vecs n‖}\)
Glossary
- direction vector
- a vector parallel to a line that is used to describe the direction, or orientation, of the line in space
- general form of the equation of a plane
- an equation in the form \(ax+by+cz+d=0,\) where \(\vecs n=⟨a,b,c⟩\) is a normal vector of the plane, \(P=(x_0,y_0,z_0)\) is a point on the plane, and \(d=−ax_0−by_0−cz_0\)
- normal vector
- a vector perpendicular to a plane
- parametric equations of a line
- the set of equations \(x=x_0+ta, y=y_0+tb,\) and \(z=z_0+tc\) describing the line with direction vector \(v=⟨a,b,c⟩\) passing through point \((x_0,y_0,z_0)\)
- scalar equation of a plane
- the equation \(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\) used to describe a plane containing point \(P=(x_0,y_0,z_0)\) with normal vector \(n=⟨a,b,c⟩\) or its alternate form \(ax+by+cz+d=0\), where \(d=−ax_0−by_0−cz_0\)
- skew lines
- two lines that are not parallel but do not intersect
- symmetric equations of a line
- the equations \(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\) describing the line with direction vector \(v=⟨a,b,c⟩\) passing through point \((x_0,y_0,z_0)\)
- vector equation of a line
- the equation \(\vecs r=\vecs r_0+t\vecs v\) used to describe a line with direction vector \(\vecs v=⟨a,b,c⟩\) passing through point \(P=(x_0,y_0,z_0)\), where \(\vecs r_0=⟨x_0,y_0,z_0⟩\), is the position vector of point \(P\)
- vector equation of a plane
- the equation \(\vecs n⋅\vecd{PQ}=0,\) where \(P\) is a given point in the plane, \(Q\) is any point in the plane, and \(\vecs n\) is a normal vector of the plane


