13.1: Vector-Valued Functions and Space Curves
- Page ID
- 2594
- Write the general equation of a vector-valued function in component form and unit-vector form.
- Recognize parametric equations for a space curve.
- Describe the shape of a helix and write its equation.
- Define the limit of a vector-valued function.
Our study of vector-valued functions combines ideas from our earlier examination of single-variable calculus with our description of vectors in three dimensions from the preceding chapter. In this section, we extend concepts from earlier chapters and also examine new ideas concerning curves in three-dimensional space. These definitions and theorems support the presentation of material in the rest of this chapter and also in the remaining chapters of the text.
Definition of a Vector-Valued Function
Our first step in studying the calculus of vector-valued functions is to define what exactly a vector-valued function is. We can then look at graphs of vector-valued functions and see how they define curves in both two and three dimensions.
A vector-valued function is a function of the form
\[\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \; \; \text{or} \; \;\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}+h(t)\,\hat{\mathbf{k}}, \nonumber \]
where the component functions \(f\), \(g\), and \(h\), are real-valued functions of the parameter \(t\). Vector-valued functions are also written in the form
\[\vecs r(t)=⟨f(t),\,g(t)⟩ \; \; \text{or} \; \; \vecs r(t)=⟨f(t),\,g(t),\,h(t)⟩. \nonumber \]
In both cases, the first form of the function defines a two-dimensional vector-valued function; the second form describes a three-dimensional vector-valued function.
The parameter \(t\) can lie between two real numbers: \(a≤t≤b\). Another possibility is that the value of \(t\) might take on all real numbers. Last, the component functions themselves may have domain restrictions that enforce restrictions on the value of \(t\). We often use \(t\) as a parameter because \(t\) can represent time.
For each of the following vector-valued functions, evaluate \(\vecs r(0)\), \(\vecs r(\frac{\pi}{2})\), and \(\vecs r(\frac{2\pi}{3})\). Do any of these functions have domain restrictions?
- \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=3\tan t\,\hat{\mathbf{i}}+4 \sec t\,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}}\)
Solution
- To calculate each of the function values, substitute the appropriate value of \(t\) into the function:
\begin{align*}\vecs r(0) \; = 4\cos(0) \hat{\mathbf{i}}+3\sin(0) \hat{\mathbf{j}} \\[4pt] =4\hat{\mathbf{i}}+0 \hat{\mathbf{j}}=4\hat{\mathbf{i}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 4\cos\left(\frac{π}{2}\right)\hat{\mathbf{i}}+3\sin\left(\frac{π}{2}\right) \hat{\mathbf{j}} \\[4pt] = 0\hat{\mathbf{i}}+3 \hat{\mathbf{j}}=3 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =4\cos\left(\frac{2π}{3}\right)\hat{\mathbf{i}}+3\sin\left(\frac{2π}{3}\right) \hat{\mathbf{j}} \\[4pt] =4\left(−\tfrac{1}{2}\right)\hat{\mathbf{i}}+3\left(\tfrac{\sqrt{3}}{2}\right) \hat{\mathbf{j}}=−2 \hat{\mathbf{i}}+\tfrac{3 \sqrt{3}}{2} \hat{\mathbf{j}}\end{align*}
To determine whether this function has any domain restrictions, consider the component functions separately. The first component function is \(f(t)=4 \cos t\) and the second component function is \(g(t)=3\sin t\). Neither of these functions has a domain restriction, so the domain of \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\) is all real numbers. - To calculate each of the function values, substitute the appropriate value of t into the function:\[\begin{align*}\vecs r(0) \; = 3\tan(0)\hat{\mathbf{i}}+4\sec(0) \hat{\mathbf{j}}+5(0) \hat{\mathbf{k}} \\[4pt] = 0\hat{\mathbf{i}}+4j+0 \hat{\mathbf{k}}=4 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 3\tan\left(\frac{\pi}{2}\right)\hat{\mathbf{i}}+4\sec\left(\frac{\pi}{2}\right) \hat{\mathbf{j}}+5\left(\frac{\pi}{2}\right) \hat{\mathbf{k}},\,\text{which does not exist} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =3\tan\left(\frac{2 \pi}{3}\right)\hat{\mathbf{i}}+4\sec\left(\frac{2\pi}{3}\right) \hat{\mathbf{j}}+5\left(\frac{2\pi}{ 3}\right) \hat{\mathbf{k}} \\[4pt] =3(−\sqrt{3})\hat{\mathbf{i}}+4(−2)\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}} \\[4pt] =(-3\sqrt{3})\hat{\mathbf{i}}−8\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}}\end{align*}\]To determine whether this function has any domain restrictions, consider the component functions separately. The first component function is \(f(t)=3\tan t\), the second component function is \(g(t)=4\sec t\), and the third component function is \(h(t)=5t\). The first two functions are not defined for odd multiples of \(\frac{\pi}{2}\), so the function is not defined for odd multiples of \(\frac{\pi}{2}\). Therefore, \[\text{D}_{\vecs r}=\Big\{t\,|\,t≠ \frac{(2n+1)\pi}{2}\Big\},\nonumber \] where \(n\) is any integer.
For the vector-valued function \(\vecs r(t)=(t^2−3t) \,\hat{\mathbf{i}}+(4t+1) \,\hat{\mathbf{j}}\), evaluate \(\vecs r(0),\, \vecs r(1)\), and \(\vecs r(−4)\). Does this function have any domain restrictions?
- Hint
-
Substitute the appropriate values of \(t\) into the function.
- Answer
-
\(\vecs r(0) = \hat{\mathbf{j}},\, \vecs r(1)=−2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}},\, \vecs r(−4)=28 \hat{\mathbf{i}}−15 \hat{\mathbf{j}}\)
The domain of \(\vecs r(t)=(t^2−3t)\hat{\mathbf{i}}+(4t+1)\hat{\mathbf{j}}\) is all real numbers.
Example \(\PageIndex{1}\) illustrates an important concept. The domain of a vector-valued function consists of real numbers. The domain can be all real numbers or a subset of the real numbers. The range of a vector-valued function consists of vectors. Each real number in the domain of a vector-valued function is mapped to either a two- or a three-dimensional vector.
Graphing Vector-Valued Functions
Recall that a plane vector consists of two quantities: direction and magnitude. Given any point in the plane (the initial point), if we move in a specific direction for a specific distance, we arrive at a second point. This represents the terminal point of the vector. We calculate the components of the vector by subtracting the coordinates of the initial point from the coordinates of the terminal point.
A vector is considered to be in standard position if the initial point is located at the origin. When graphing a vector-valued function, we typically graph the vectors in the domain of the function in standard position, because doing so guarantees the uniqueness of the graph. This convention applies to the graphs of three-dimensional vector-valued functions as well. The graph of a vector-valued function of the form
\[\vecs r(t)=f(t)\, \hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \nonumber \]
consists of the set of all points \((f(t),\,g(t))\), and the path it traces is called a plane curve. The graph of a vector-valued function of the form
\[\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}} \nonumber \]
consists of the set of all points \((f(t),\,g(t),\,h(t))\), and the path it traces is called a space curve. Any representation of a plane curve or space curve using a vector-valued function is called a vector parameterization of the curve.
Each plane curve and space curve has an orientation, indicated by arrows drawn in on the curve, that shows the direction of motion along the curve as the value of the parameter \(t\) increases.
Create a graph of each of the following vector-valued functions:
- The plane curve represented by \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\), \(0≤t≤2\pi\)
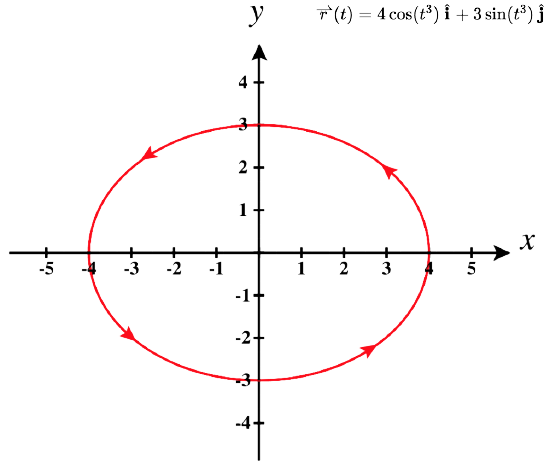
- The plane curve represented by \(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\), \(0≤t≤\sqrt[3]{2\pi}\)
- The space curve represented by \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), \(0≤t≤4\pi\)
Solution
1. As with any graph, we start with a table of values. We then graph each of the vectors in the second column of the table in standard position and connect the terminal points of each vector to form a curve (Figure \(\PageIndex{1}\)). This curve turns out to be an ellipse centered at the origin.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \(0\) | \(4\hat{\mathbf{i}}\) | \(\pi\) | \(-4\hat{\mathbf{i}}\) |
| \(\dfrac{\pi}{4}\) | \(2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \(\dfrac{5\pi}{4}\) | \(-2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \(\dfrac{\pi}{2}\) | \(\mathrm{3\hat{\mathbf{j}}}\) | \(\dfrac{3\pi}{2}\) | \(\mathrm{-3\hat{\mathbf{j}}}\) |
| \(\dfrac{3\pi}{4}\) | \( -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \(\dfrac{7\pi}{4}\) | \( 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \(2\pi\) | \(4\hat{\mathbf{i}}\) |
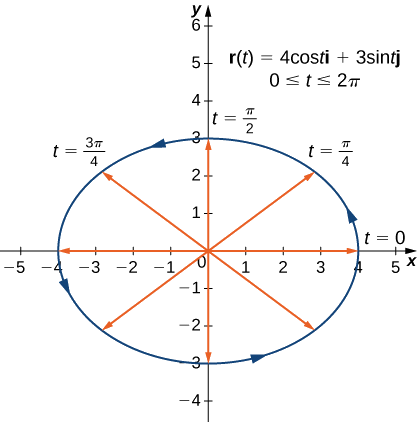
2. The table of values for \(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\), \(0≤t≤\sqrt[3]{2\pi}\) is as follows:
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \(0\) | \(\mathrm{4\hat{\mathbf{i}}}\) | \(\displaystyle\sqrt[3]{\pi}\) | \(\mathrm{-4\hat{\mathbf{i}}}\) |
| \(\displaystyle \sqrt[3]{\dfrac{\pi}{4}}\) | \(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \(\displaystyle \sqrt[3]{\dfrac{5\pi}{4}}\) | \(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \(\displaystyle \sqrt[3]{\dfrac{\pi}{2}}\) | \(\mathrm{3\hat{\mathbf{j}}}\) | \(\displaystyle \sqrt[3]{\dfrac{3\pi}{2}}\) | \(\mathrm{-3\hat{\mathbf{j}}}\) |
| \(\displaystyle \sqrt[3]{\dfrac{3\pi}{4}}\) | \(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \(\displaystyle \sqrt[3]{\dfrac{7\pi}{4}}\) | \(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \( \displaystyle\sqrt[3]{2\pi}\) | \(\mathrm{4\hat{\mathbf{i}}}\) |
The graph of this curve is also an ellipse centered at the origin.
3. We go through the same procedure for a three-dimensional vector function.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \(\mathrm{0}\) | \(\mathrm{4\hat{\mathbf{i}}}\) | \(\mathrm{\pi}\) | \(\mathrm{-4\hat{\mathbf{i}}}+ \pi \hat{\mathbf{k}}\) |
| \(\dfrac{\pi}{4}\) | \(\mathrm{2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{\pi}{4} \hat{\mathbf{k}}}\) | \(\dfrac{5\pi}{4}\) | \(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{5\pi}{4} \hat{\mathbf{k}}}\) |
| \(\dfrac{\pi}{2}\) | \(\mathrm{4\hat{\mathbf{j}} +\frac{\pi}{2} \hat{\mathbf{k}}}\) | \(\dfrac{3\pi}{2}\) | \(\mathrm{-4\hat{\mathbf{j}} +\frac{3\pi}{2} \hat{\mathbf{k}}}\) |
| \(\dfrac{3\pi}{4}\) | \(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{3\pi}{4} \hat{\mathbf{k}}}\) | \(\dfrac{7\pi}{4}\) | \(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{7\pi}{4} \hat{\mathbf{k}}}\) |
| \(\mathrm{2\pi}\) | \(\mathrm{4\hat{\mathbf{j}} + 2\pi \hat{\mathbf{k}}}\) |
The values then repeat themselves, except for the fact that the coefficient of \(\hat{\mathbf{k}}\) is always increasing ( \(\PageIndex{3}\)). This curve is called a helix. Notice that if the \(\hat{\mathbf{k}}\) component is eliminated, then the function becomes \(\vecs r(t)=4\cos t \hat{\mathbf{i}}+ 4\sin t \hat{\mathbf{j}}\), which is a circle of radius 4 centered at the origin.

You may notice that the graphs in parts a. and b. are identical. This happens because the function describing curve b is a so-called reparameterization of the function describing curve a. In fact, any curve has an infinite number of reparameterizations; for example, we can replace \(t\) with \(2t\) in any of the three previous curves without changing the shape of the curve. The interval over which \(t\) is defined may change, but that is all. We return to this idea later in this chapter when we study arc-length parameterization. As mentioned, the name of the shape of the curve of the graph in \(\PageIndex{3}\) is a helix. The curve resembles a spring, with a circular cross-section looking down along the \(z\)-axis. It is possible for a helix to be elliptical in cross-section as well. For example, the vector-valued function \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) describes an elliptical helix. The projection of this helix into the \(xy\)-plane is an ellipse. Last, the arrows in the graph of this helix indicate the orientation of the curve as \(t\) progresses from \(0\) to \(4π\).
Create a graph of the vector-valued function \(\vecs r(t)=(t^2−1)\hat{\mathbf{i}}+(2t−3) \hat{\mathbf{j}}\), \(0≤t≤3\).
- Hint
-
Start by making a table of values, then graph the vectors for each value of \(t\).
- Answer
-
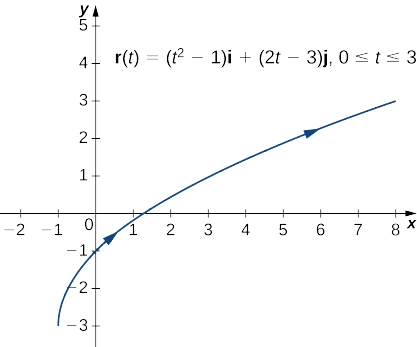
At this point, you may notice a similarity between vector-valued functions and parameterized curves. Indeed, given a vector-valued function \(\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}\) we can define \(x=f(t)\) and \(y=g(t)\). If a restriction exists on the values of \(t\) (for example, \(t\) is restricted to the interval \([a,b]\) for some constants \(a<b\), then this restriction is enforced on the parameter. The graph of the parameterized function would then agree with the graph of the vector-valued function, except that the vector-valued graph would represent vectors rather than points. Since we can parameterize a curve defined by a function \(y=f(x)\), it is also possible to represent an arbitrary plane curve by a vector-valued function.
Limits and Continuity of a Vector-Valued Function
We now take a look at the limit of a vector-valued function. This is important to understand to study the calculus of vector-valued functions.
A vector-valued function \(\vecs r\) approaches the limit \(\vecs L\) as \(t\) approaches \(a\), written
\[\lim \limits_{t \to a} \vecs r(t) = \vecs L, \nonumber \]
provided
\[\lim \limits_{t \to a} \big\| \vecs r(t) - \vecs L \big\| = 0. \nonumber \]
This is a rigorous definition of the limit of a vector-valued function. In practice, we use the following theorem:
Let \(f\), \(g\), and \(h\) be functions of \(t\). Then the limit of the vector-valued function \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) as t approaches a is given by
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} , \label{Th1} \]
provided the limits \(\lim \limits_{t \to a} f(t)\) and \(\lim \limits_{t \to a} g(t)\) exist.
Similarly, the limit of the vector-valued function \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) as \(t\) approaches \(a\) is given by
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} +[\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}} , \label{Th2} \]
provided the limits \(\lim \limits_{t \to a} f(t)\), \(\lim \limits_{t \to a} g(t)\) and \(\lim \limits_{t \to a} h(t)\) exist.
In the following example, we show how to calculate the limit of a vector-valued function.
For each of the following vector-valued functions, calculate \(\lim \limits_{t \to 3}\vecs r(t)\) for
- \(\vecs r(t)=(t^2−3t+4) \hat{\mathbf{i}}+(4t+3)\hat{\mathbf{j}}\)
- \(\vecs r(t)=\frac{2t−4}{t+1}\hat{\mathbf{i}}+\frac{t}{t^2+1} \hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\)
Solution
- Use Equation \ref{Th1} and substitute the value \(t=3\) into the two component expressions:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3} \left[(t^2−3t+4) \hat{\mathbf{i}} + (4t+3) \hat{\mathbf{j}}\right] \\[4pt] = \left[\lim \limits_{t \to 3} (t^2−3t+4)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} (4t+3)\right] \hat{\mathbf{j}} \\[4pt] = 4 \hat{\mathbf{i}}+15 \hat{\mathbf{j}} \end{align*}\]
- Use Equation \ref{Th2} and substitute the value \(t=3\) into the three component expressions:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3}\left(\dfrac{2t−4}{t+1}\hat{\mathbf{i}}+\dfrac{t}{t^2+1}\hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\right) \\[4pt] = \left[\lim \limits_{t \to 3} \left(\dfrac{2t−4}{t+1}\right)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} \left(\dfrac{t}{t^2+1}\right)\right] \hat{\mathbf{j}} +\left[\lim \limits_{t \to 3} (4t−3)\right] \hat{\mathbf{k}} \\[4pt] = \tfrac{1}{2} \hat{\mathbf{i}}+\tfrac{3}{10}\hat{\mathbf{j}}+9 \hat{\mathbf{k}} \end{align*}\]
Calculate \(\lim \limits_{t \to 2} \vecs r(t)\) for the function \(\vecs r(t) = \sqrt{t^2 + 3t - 1}\,\hat{\mathbf{i}}−(4t-3)\hat{\mathbf{j}}− \sin \frac{(t+1)\pi}{2}\hat{\mathbf{k}}\)
- Hint
-
Use Equation \ref{Th2} from the preceding theorem.
- Answer
-
\[\lim \limits_{t \to 2} \vecs r(t) = 3\hat{\mathbf{i}}−5\hat{\mathbf{j}}+\hat{\mathbf{k}} \nonumber \]
Now that we know how to calculate the limit of a vector-valued function, we can define continuity at a point for such a function.
Let \(f\), \(g\), and \(h\) be functions of \(t\). Then, the vector-valued function \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) is continuous at point \(t=a\) if the following three conditions hold:
- \(\vecs r(a)\) exists
- \(\lim \limits_{t \to a} \vecs r(t)\) exists
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Similarly, the vector-valued function \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) is continuous at point \(t=a\) if the following three conditions hold:
- \(\vecs r(a)\) exists
- \(\lim \limits_{t \to a} \vecs r(t)\) exists
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Summary
- A vector-valued function is a function of the form \(\vecs r(t)=f(t) \hat{\mathbf{i}}+ g(t) \hat{\mathbf{j}}\) or \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), where the component functions \(f\), \(g\), and \(h\) are real-valued functions of the parameter \(t\).
- The graph of a vector-valued function of the form \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) is called a plane curve. The graph of a vector-valued function of the form \(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) is called a space curve.
- It is possible to represent an arbitrary plane curve by a vector-valued function.
- To calculate the limit of a vector-valued function, calculate the limits of the component functions separately.
Key Equations
- Vector-valued function
\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) or \(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\),or \(\vecs r(t)=⟨f(t),g(t)⟩\) or \(\vecs r(t)=⟨f(t),g(t),h(t)⟩\) - Limit of a vector-valued function
\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}}\) or \(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} + [\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}}\)
Glossary
- component functions
- the component functions of the vector-valued function \(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) are \(f(t)\) and \(g(t)\), and the component functions of the vector-valued function \(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) are \(f(t)\), \(g(t)\) and \(h(t)\)
- helix
- a three-dimensional curve in the shape of a spiral
- limit of a vector-valued function
- a vector-valued function \(\vecs r(t)\) has a limit \(\vecs L\) as \(t\) approaches \(a\) if \(\lim \limits{t \to a} \left| \vecs r(t) - \vecs L \right| = 0\)
- plane curve
- the set of ordered pairs \((f(t),g(t))\) together with their defining parametric equations \(x=f(t)\) and \(y=g(t)\)
- reparameterization
- an alternative parameterization of a given vector-valued function
- space curve
- the set of ordered triples \((f(t),g(t),h(t))\) together with their defining parametric equations \(x=f(t)\), \(y=g(t)\) and \(z=h(t)\)
- vector parameterization
- any representation of a plane or space curve using a vector-valued function
- vector-valued function
- a function of the form \(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) or \(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\),where the component functions \(f\), \(g\), and \(h\) are real-valued functions of the parameter \(t\).
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Edited by Paul Seeburger (Monroe Community College)


