15.4E: Exercises for Section 15.4
- Page ID
- 67165
In exercises 1 - 4, evaluate the triple integrals over the rectangular solid box \(B\).
1. \(\displaystyle \iiint_B (2x + 3y^2 + 4z^3) \, dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 2, \, 0 \leq z \leq 3\big\}\)
- Answer
- \(192\)
2. \(\displaystyle \iiint_B (xy + yz + xz) \, dV,\) where \(B = \big\{(x,y,z) \,|\, 1 \leq x \leq 2, \, 0 \leq y \leq 2, \, 1 \leq z \leq 3\big\}\)
3. \(\displaystyle \iiint_B (x \cos y + z) \, dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq \pi, \, -1 \leq z \leq 1\big\}\)
- Answer
- \(0\)
4. \(\displaystyle \iiint_B (z \sin x + y^2) \, dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq \pi, \, 0 \leq y \leq 1, \, -1 \leq z \leq 2\big\}\)
In exercises 5 - 8, change the order of integration by integrating first with respect to \(z\), then \(x\), then \(y\).
5. \(\displaystyle \int_0^1 \int_1^2 \int_2^3 (x^2 + \ln y + z) \, dx \, dy \, dz\)
- Answer
- \(\displaystyle \int_0^1 \int_1^2 \int_2^3 (x^2 + \ln y + z) \, dx \, dy \, dz = \frac{35}{6} + 2 \ln 2\)
6. \(\displaystyle \int_0^1 \int_{-1}^1 \int_0^3 (ze^x + 2y) \, dx \, dy \, dz\)
7. \(\displaystyle \int_{-1}^2 \int_1^3 \int_0^4 \left(x^2z + \frac{1}{y}\right) \, dx \, dy \, dz\)
- Answer
- \(\displaystyle \int_{-1}^2 \int_1^3 \int_0^4 \left(x^2z + \frac{1}{y}\right) \, dx \, dy \, dz = 64 + 12 \ln 3\)
8. \(\displaystyle \int_1^2 \int_{-2}^{-1} \int_0^1 \frac{x + y}{z} \, dx \, dy \, dz\)
9. Let \(F\), \(G\), and \(H\) be continuous functions on \([a,b]\), \([c,d]\), and \([e,f]\), respectively, where \(a, \, b, \, c, \, d, \, e\), and \(f\) are real numbers such that \(a < b, \, c < d\), and \(e < f\). Show that
\[\int_a^b \int_c^d \int_e^f F (x) \, G (y) \, H(z) \, dz \, dy \, dx = \left(\int_a^b F(x) \, dx \right) \left(\int_c^d G(y) \, dy \right) \left(\int_e^f H(z) \, dz \right).\nonumber \]
10. Let \(F\), \(G\), and \(H\) be differential functions on \([a,b]\), \([c,d]\), and \([e,f]\), respectively, where \(a, \, b, \, c, \, d, \, e\), and \(f\) are real numbers such that \(a < b, \, c < d\), and \(e < f\). Show that
\[\int_a^b \int_c^d \int_e^f F' (x) \, G' (y) \, H'(z) \, dz \, dy \, dx = [F (b) - F (a)] \, [G(d) - G(c)] \, H(f) - H(e)].\nonumber \]
In exercises 11 - 14, evaluate the triple integrals over the bounded region
\(E = \big\{(x,y,z) \,|\, a \leq x \leq b, \, h_1 (x) \leq y \leq h_2 (x), \, e \leq z \leq f \big\}.\)
11. \(\displaystyle \iiint_E (2x + 5y + 7z) \, dV, \) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq -x + 1, \, 1 \leq z \leq 2\big\}\)
- Answer
- \(\frac{77}{12}\)
12. \(\displaystyle \iiint_E (y \ln x + z) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 1 \leq x \leq e, \, 0 \leq y \ln x, \, 0 \leq z \leq 1\big\}\)
13. \(\displaystyle \iiint_E (\sin x + \sin y) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \frac{\pi}{2}, \, -\cos x \leq y \cos x, \, -1 \leq z \leq 1 \big\}\)
- Answer
- \(2\)
14. \(\displaystyle \iiint_E (xy + yz + xz ) dV\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, -x^2 \leq y \leq x^2, \, 0 \leq z \leq 1 \big\}\)
In exercises 15 - 18, evaluate the triple integrals over the indicated bounded region \(E\).
15. \(\displaystyle \iiint_E (x + 2yz) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x, \, 0 \leq z \leq 5 - x - y \big\}\)
- Answer
- \(\frac{430}{120}\)
16. \(\displaystyle \iiint_E (x^3 + y^3 + z^3) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 2, \, 0 \leq y \leq 2x, \, 0 \leq z \leq 4 - x - y \big\}\)
17. \(\displaystyle \iiint_E y \, dV,\) where \(E = \big\{(x,y,z) \,|\, -1 \leq x \leq 1, \, -\sqrt{1 - x^2} \leq y \leq \sqrt{1 - x^2}, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)
- Answer
- \(0\)
18. \(\displaystyle \iiint_E x \, dV,\) where \(E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, -4\sqrt{1 - x^2} \leq y \leq \sqrt{4 - x^2}, \, 0 \leq z \leq 4 - x^2 - y^2 \big\}\)
In exercises 19 - 22, evaluate the triple integrals over the bounded region \(E\) of the form
\(E = \big\{(x,y,z) \,|\, g_1 (y) \leq x \leq g_2(y), \, c \leq y \leq d, \, e \leq z \leq f \big\}\).
19. \(\displaystyle \iiint_E x^2 \, dV,\) where \(E = \big\{(x,y,z) \,|\, 1 - y^2 \leq x \leq y^2 - 1, \, -1 \leq y \leq 1, \, 1 \leq z \leq 2 \big\}\)
- Answer
- \(-\frac{64}{105}\)
20. \(\displaystyle \iiint_E (y + \sin x) \, dV,\) where \(E = \big\{(x,y,z) \,|\, -y^4 \leq x \leq y^4, \, 0 \leq y \leq 2, \, 0 \leq z \leq 4\big\}\)
21. \(\displaystyle \iiint_E (x - yz) \, dV,\) where \(E = \big\{(x,y,z) \,|\, -y^6 \leq x \leq \sqrt{y}, \, 0 \leq y \leq 1x, \, -1 \leq z \leq 1 \big\}\)
- Answer
- \(\frac{11}{26}\)
22. \(\displaystyle \iiint_E z \, dV,\) where \(E = \big\{(x,y,z) \,|\, 2 - 2y \leq x \leq 2 + \sqrt{y}, \, 0 \leq y \leq 1x, \, 2 \leq z \leq 3 \big\}\)
In exercises 23 - 26, evaluate the triple integrals over the bounded region
\(E = \big\{(x,y,z) \,|\, g_1(y) \leq x \leq g_2(y), \, c \leq y \leq d, \, u_1(x,y) \leq z \leq u_2 (x,y) \big\}\)
23. \(\displaystyle \iiint_E z \, dV,\) where \(E = \big\{(x,y,z) \,|\, -y \leq x \leq y, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 - x^4 - y^4 \big\}\)
- Answer
- \(\frac{113}{450}\)
24. \(\displaystyle \iiint_E (xz + 1) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \sqrt{y}, \, 0 \leq y \leq 2, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)
25. \(\displaystyle \iiint_E (x - z) \, dV,\) where \(E = \big\{(x,y,z) \,|\, - \sqrt{1 - y^2} \leq x \leq y, \, 0 \leq y \leq \frac{1}{2}x, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)
- Answer
- \(\frac{1}{160}(6 \sqrt{3} - 41)\)
26. \(\displaystyle \iiint_E (x + y) \, dV,\) where \(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \sqrt{1 - y^2}, \, 0 \leq y \leq 1x, \, 0 \leq z \leq 1 - x \big\}\)
In exercises 27 - 30, evaluate the triple integrals over the bounded region
\(E = \big\{(x,y,z) \,|\, (x,y) \in D, \, u_1 (x,y) x \leq z \leq u_2 (x,y) \big\}\), where \(D\) is the projection of \(E\) onto the \(xy\)-plane.
27. \(\displaystyle \iint_D \left(\int_1^2 (x + y) \, dz \right) \, dA,\) where \(D = \big\{(x,y) \,|\, x^2 + y^2 \leq 1\big\}\)
- Answer
- \(\frac{3\pi}{2}\)
28. \(\displaystyle \iint_D \left(\int_1^3 x (z + 1)\, dz \right) \, dA,\) where \(D = \big\{(x,y) \,|\, x^2 -y^2 \geq 1, \, x \leq \sqrt{5}\big\}\)
29. \(\displaystyle \iint_D \left(\int_0^{10-x-y} (x + 2z) \, dz \right) \, dA,\) where \(D = \big\{(x,y) \,|\, y \geq 0, \, x \geq 0, \, x + y \leq 10\big\}\)
- Answer
- \(1250\)
30. \(\displaystyle \iint_D \left(\int_0^{4x^2+4y^2} y \, dz \right) \, dA,\) where \(D = \big\{(x,y) \,|\, x^2 + y^2 \leq 4, \, y \geq 1, \, x \geq 0\big\}\)
31. The solid \(E\) bounded by \(y^2 + z^2 = 9, \, z = 0\), and \(x = 5\) is shown in the following figure. Evaluate the integral \(\displaystyle \iiint_E z \, dV\) by integrating first with respect to \(z\), then \(y\), and then \(x\).
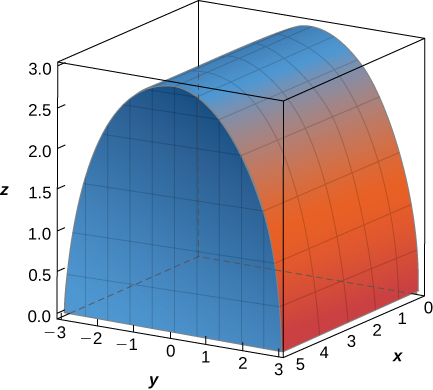
- Answer
- \(\displaystyle \int_0^5 \int_{-3}^3 \int_0^{\sqrt{9-y^2}} z \, dz \, dy \, dx = 90\)
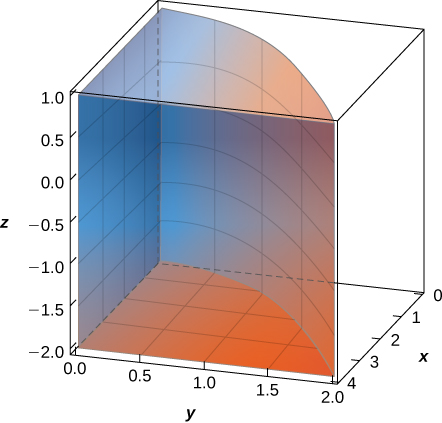
32. The solid \(E\) bounded by \(y = \sqrt{x}, \, x = 4, \, y = 0\), and \(z = 1\) is given in the following figure. Evaluate the integral \(\displaystyle \iiint_E xyz \, dV\) by integrating first with respect to \(x\), then \(y\), and then \(z\).
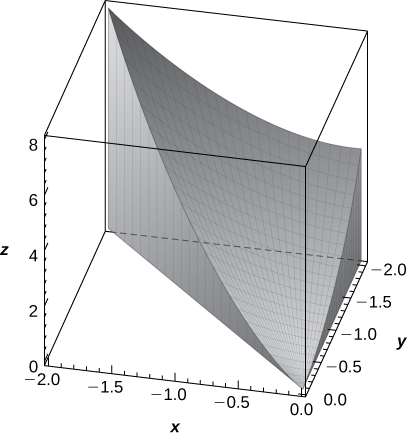
33. [T] The volume of a solid \(E\) is given by the integral \(\displaystyle \int_{-2}^0 \int_x^0 \int_0^{x^2+y^2} \, dz \, dy \, dx.\) Use a computer algebra system (CAS) to graph \(E\) and find its volume. Round your answer to two decimal places.
- Answer
- \(V \approx 5.33 \text{ units}^3\)
34. [T] The volume of a solid \(E\) is given by the integral \(\displaystyle \int_{-1}^0 \int_{-x^3}^0 \int_0^{1+\sqrt{x^2+y^2}} \, dz \, dy \, dx.\) Use a CAS to graph \(E\) and find its volume \(V\). Round your answer to two decimal places.
In exercises 35 - 38, use two circular permutations of the variables \(x\), \(y\), and \(z\) to write new integrals whose values equal the value of the original integral. A circular permutation of \(x, \, y\), and \(z\) is the arrangement of the numbers in one of the following orders: \(y\), \(z\), and \(x\) or \(z\), \(x\), and \(y\).
35. \(\displaystyle \int_0^1 \int_1^3 \int_2^4 (x^2z^2 + 1) \, dx \, dy \, dz\)
- Answer
- \(\displaystyle \int_0^1 \int_1^3 \int_2^4 (y^2z^2 + 1) \, dz \, dx \, dy;\)
\(\displaystyle \int_0^1 \int_1^3 \int_2^4 (x^2y^2 + 1) \, dy \, dz \, dx\)
36. \(\displaystyle \int_0^3 \int_0^1 \int_0^{-x+1} (2x + 5y + 7z) dy \, dx \, dz\)
37. \(\displaystyle \int_0^1 \int_{-y}^y \int_0^{1-x^4-y^4} \ln x \, dz \, dx \, dy\)
38. \(\displaystyle \int_{-1}^1 \int_0^1 \int_{-y^6}^{\sqrt{y}} (x + yz) \, dx \, dy \, dz\)
39. Set up the integral that gives the volume of the solid \(E\) bounded by \(y^2 = x^2 + z^2\) and \(y = a^2\), where \(a > 0\).
- Answer
- \(\displaystyle V = \int_{-a}^a \int_{-\sqrt{a^2-z^2}}^{\sqrt{a^2-z^2}} \int_{\sqrt{x^2+z^2}}^{a^2} \, dy \, dx \, dz\)
40. Set up the integral that gives the volume of the solid \(E\) bounded by \(x = y^2 + z^2\) and \(x = a^2\), where \(a > 0\).
Average Value of a Function
41. Find the average value of the function \(f(x,y,z) = x + y + z\) over the parallelepiped determined by \(x + 0, \, x = 1, \, y = 0, \, y = 3, \, z = 0\), and \(z = 5\).
- Answer
- \(\frac{9}{2}\)
42. Find the average value of the function \(f(x,y,z) = xyz\) over the solid \(E = [0,1] \times [0,1] \times [0,1]\) situated in the first octant.
Finding Volumes using Triple Integrals
43. Find the volume of the solid \(E\) that lies under the plane \(x + y + z = 9\) and whose projection onto the \(xy\)-plane is bounded by \(x = sqrt{y-1}, \, x = 0\), and \(x + y = 7\).
- Answer
- \(\frac{156}{5} \text{ units}^3\)
44. Find the volume of the solid \(E\) that lies under the plane \(2x+y+z=8\) and whose projection onto the \(xy\)-plane is bounded by \(x = sin^{-1} y, \, y = 0\), and \(x = \frac{\pi}{2}\).
a. Show that the equations of the planes of the lateral faces of the pyramid are \(4y + z = 8, \, 4y - z = -8, \, 4x + z = 8\), and \(-4x + z = 8\).
b. Find the volume of the pyramid.
- Answer
- a. Answers may vary;
b. \(\frac{128}{3} \text{ units}^3\)
46. Consider the pyramid with the base in the \(xy\)-plane of \([-3,3] \times [-3,3]\) and the vertex at the point \((0,0,9)\).
a. Show that the equations of the planes of the side faces of the pyramid are \(3y + z = 9, \, 3y + z = 9, \, y = 0\) and \(x = 0\).
b. Find the volume of the pyramid.
47. The solid \(E\) bounded by the sphere of equation \(x^2 + y^2 + z^2 = r^2\) with \(r > 0\) and located in the first octant is represented in the following figure.
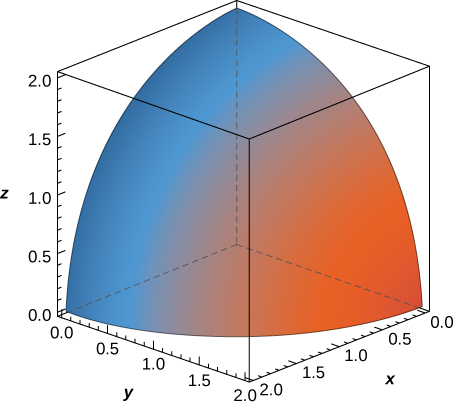
a. Write the triple integral that gives the volume of \(E\) by integrating first with respect to \(z\), then with \(y\), and then with \(x\).
b. Rewrite the integral in part a. as an equivalent integral in five other orders.
- Answer
-
a. \(\displaystyle \int_0^4 \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dz \, dy \, dx\)
b. \(\displaystyle \int_0^2 \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dz \, dx \, dy,\)
\(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dy \, dx \, dz,\)
\(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dy \, dz \, dx,\)
\(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dx \, dy \, dz,\)
\(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dx \, dz \,dy\)
48. The solid \(E\) bounded by the sphere of equation \(9x^2 + 4y^2 + z^2 = 1\) and located in the first octant is represented in the following figure.
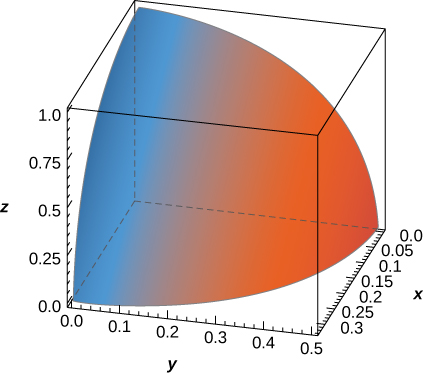
a. Write the triple integral that gives the volume of \(E\) by integrating first with respect to \(z\) then with \(y\) and then with \(x\).
b. Rewrite the integral in part a. as an equivalent integral in five other orders.
49. Find the volume of the prism with vertices \((0,0,0), \, (2,0,0), \, (2,3,0), \, (0,3,0), \, (0,0,1)\), and \((2,0,1)\).
- Answer
- \(3 \text{ units}^3\)
50. Find the volume of the prism with vertices \((0,0,0), \, (4,0,0), \, (4,6,0), \, (0,6,0), \, (0,0,1)\), and \((4,0,1)\).
51. The solid \(E\) bounded by \(z = 10 - 2x - y\) and situated in the first octant is given in the following figure. Find the volume of the solid.
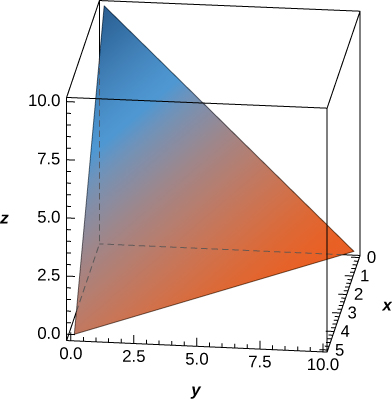
- Answer
- \(\frac{250}{3} \text{ units}^3\)
52. The solid \(E\) bounded by \(z = 1 - x^2\) and situated in the first octant is given in the following figure. Find the volume of the solid.
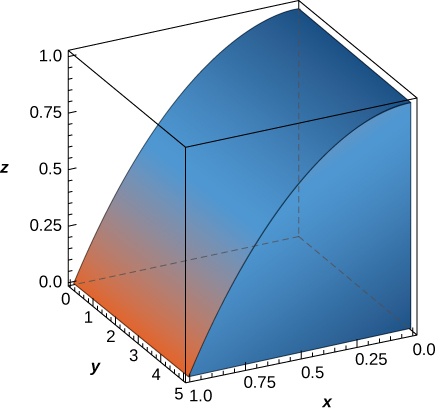
Approximating Triple Integrals
53. The midpoint rule for the triple integral \(\displaystyle \iiint_B f(x,y,z) \,dV\) over the rectangular solid box \(B\) is a generalization of the midpoint rule for double integrals. The region \(B\) is divided into subboxes of equal sizes and the integral is approximated by the triple Riemann sum \[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\bar{x_i}, \bar{y_j}, \bar{z_k}) \Delta V,\nonumber \] where \((\bar{x_i}, \bar{y_j}, \bar{z_k})\) is the center of the box \(B_{ijk}\) and \(\Delta V\) is the volume of each subbox. Apply the midpoint rule to approximate \[\iiint_B x^2 \,dV\nonumber \] over the solid \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \big\}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.
- Answer
- \(\displaystyle \iiint_B f(x,y,z) \,dV\quad\) \(\approx\quad\frac{5}{16} \approx 0.313 \text{ units}^3\)
54. [T]
a. Apply the midpoint rule to approximate \(\displaystyle \iiint_B e^{-x^2} \, dV\) over the solid \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \big\}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.
b. Use a CAS to improve the above integral approximation in the case of a partition of \(n^3\) cubes of equal size, where \(n = 3,\,4,\, ..., \,10\).
Applications
55. Suppose that the temperature in degrees Celsius at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T (x,y,z) = xz + 5z + 10\nonumber \] Find the average temperature over the solid.
- Answer
- \(17.5^{\circ}\) C
56. Suppose that the temperature in degrees Fahrenheit at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T(x,y,z) = x + y + xy\nonumber \] Find the average temperature over the solid.
57. Show that the volume of a right square pyramid of height \(h\) and side length \(a\) is \( v = \dfrac{ha^2}{3}\) by using triple integrals.
58. Show that the volume of a regular right hexagonal prism of edge length \(a\) is \(\dfrac{3a^3 \sqrt{3}}{2}\) by using triple integrals.
59. Show that the volume of a regular right hexagonal pyramid of edge length \(a\) is \(\dfrac{a^3 \sqrt{3}}{2}\) by using triple integrals.
60. If the charge density at an arbitrary point \((x,y,z)\) of a solid \(E\) is given by the function \(\rho (x,y,z)\), then the total charge inside the solid is defined as the triple integral \(\displaystyle \iiint_E \rho (x,y,z) \,dV.\) Assume that the charge density of the solid \(E\) enclosed by the paraboloids \(x = 5 - y^2 - z^2\) and \(x = y^2 + z^2 - 5\) is equal to the distance from an arbitrary point of \(E\) to the origin. Set up the integral that gives the total charge inside the solid \(E\).
- Answer
- Total Charge inside the Solid \(E \quad=\quad\) \(\displaystyle \int_{-\sqrt{5}}^{\sqrt{5}}\int_{-\sqrt{5-y^2}}^{\sqrt{5-y^2}}\int_{y^2+z^2-5}^{5 - y^2 - z^2} \sqrt{x^2+y^2+z^2}\,dx\,dz\,dy\)


