1.2: Vector Algebra
- Page ID
- 2213
Now that we know what vectors are, we can start to perform some of the usual algebraic operations on them (e.g. addition, subtraction). Before doing that, we will introduce the notion of a scalar.
Definition 1.3
A scalar is a quantity that can be represented by a single number.
For our purposes, scalars will always be real numbers. The term scalar was invented by \(19^{th}\) century Irish mathematician, physicist and astronomer William Rowan Hamilton, to convey the sense of something that could be represented by a point on a scale or graduated ruler. The word vector comes from Latin, where it means "carrier''. Examples of scalar quantities are mass, electric charge, and speed (not velocity). We can now define scalar multiplication of a vector.
Definition 1.4
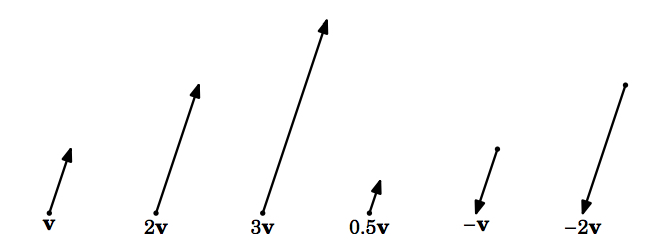
For a scalar \(k\) and a nonzero vector \(\textbf{v}\), the \(\textbf{scalar multiple}\) of \(\textbf{v}\) by \(k\), denoted by \(k\textbf{v}\), is the vector whose magnitude is \(|k| \,\norm{\textbf{v}}\), points in the same direction as \(\textbf{v}\) if \(k > 0\), points in the opposite direction as \(\textbf{v}\) if \(k < 0\), and is the zero vector \(\textbf{0}\) if \(k = 0\). For the zero vector \(\textbf{0}\), we define \(k \textbf{0} = \textbf{0}\) for any scalar \(k\).
Two vectors \(\textbf{v}\) and \(\textbf{w}\) are \(\textbf{parallel}\) (denoted by \(\textbf{v} \parallel \textbf{w}\)) if one is a scalar multiple of the other. You can think of scalar multiplication of a vector as stretching or shrinking the vector, and as flipping the vector in the opposite direction if the scalar is a negative number (Figure 1.2.1).
Recall that \(\textbf{translating}\) a nonzero vector means that the initial point of the vector is changed but the magnitude and direction are preserved. We are now ready to define the \(\textit{sum}\) of two vectors.
Definition 1.5
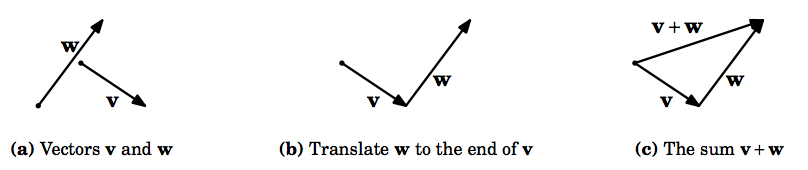
The \(\textbf{sum}\) of vectors \(\textbf{v}\) and \(\textbf{w}\), denoted by \(\textbf{v} + \textbf{w}\), is obtained by translating \(\textbf{w}\) so that its initial point is at the terminal point of \(\textbf{v}\); the initial point of \(\textbf{v} + \textbf{w}\) is the initial point of \(\textbf{v}\), and its terminal point is the new terminal point of \(\textbf{w}\).
Intuitively, adding \(\textbf{w}\) to \(\textbf{v}\) means tacking on \(\textbf{w}\) to the end of \(\textbf{v}\) (see Figure 1.2.2).
Notice that our definition is valid for the zero vector (which is just a point, and hence can be translated), and so we see that \(\textbf{v} + \textbf{0} = \textbf{v} = \textbf{0} + \textbf{v}\) for any vector \(\textbf{v}\). In particular, \(\textbf{0} + \textbf{0} = \textbf{0}\). Also, it is easy to see that \(\textbf{v} + (-\textbf{v}) = \textbf{0}\), as we would expect. In general, since the scalar multiple \(-\textbf{v} = -1 \,\textbf{v}\) is a well-defined vector, we can define \(\textbf{vector subtraction}\) as follows: \(\textbf{v} - \textbf{w} = \textbf{v} + (-\textbf{w})\) (Figure 1.2.3).
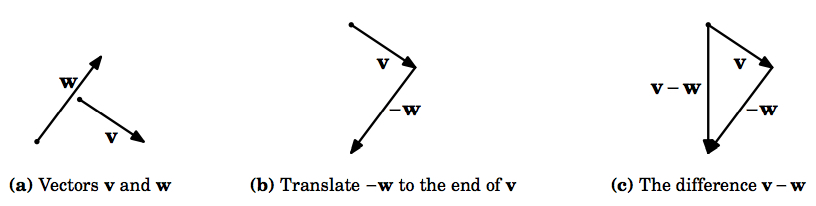
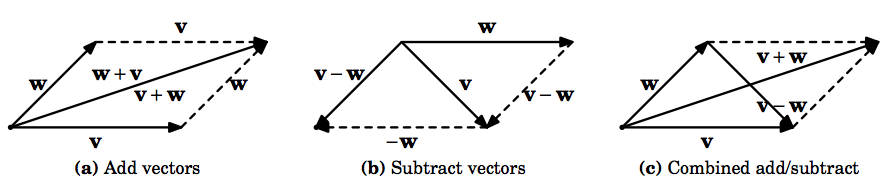
Figure 1.2.4 shows the use of "geometric proofs'' of various laws of vector algebra, that is, it uses laws from elementary geometry to prove statements about vectors. For example, (a) shows that \(\textbf{v} + \textbf{w} = \textbf{w} + \textbf{v}\) for any vectors \(\textbf{v}\), \(\textbf{w}\). And (c) shows how you can think of \(\textbf{v} - \textbf{w}\) as the vector that is tacked on to the end of
\(\textbf{w}\) to add up to \(\textbf{v}\).
Notice that we have temporarily abandoned the practice of starting vectors at the origin. In fact, we have not even mentioned coordinates in this section so far. Since we will deal mostly with Cartesian coordinates in this book, the following two theorems are useful for performing vector algebra on vectors in \(\mathbb{R}^{2}\) and \(\mathbb{R}^{3}\) starting at the origin.
Theorem 1.3
Let \(\textbf{v} = (v_{1}, v_{2})\), \(\textbf{w} = (w_{1}, w_{2})\) be vectors in \(\mathbb{R}^{2}\), and let \(k\) be a scalar. Then
- \(k\textbf{v} = (kv_{1}, kv_{2})\)
- \(\textbf{v + w} = (v_{1} + w_{1}, v_{2} + w_{2})\)
Proof: (a) Without loss of generality, we assume that \(v_{1}, v_{2} > 0\) (the other possibilities are handled in a similar manner). If \(k = 0\) then \(k\textbf{v} = 0\textbf{v} = \textbf{0} = (0,0) = (0v_{1}, 0v_{2}) = (kv_{1}, kv_{2})\), which is what we needed to show. If \(k \ne 0\), then \((kv_{1}, kv_{2})\) lies on a line with slope \(\frac{kv_{2}}{kv_{1}} = \frac{v_{2}}{v_{1}}\), which is the same as the slope of the line on which \(\textbf{v}\) (and hence \(k\textbf{v}\)) lies, and \((kv_{1}, kv_{2})\) points in the same direction on that line as \(k\textbf{v}\). Also, by formula (1.3) the magnitude of \((kv_{1}, kv_{2})\) is \(\sqrt{(kv_{1})^{2} + (kv_{2})^{2}} = \sqrt{k^{2} v_{1}^{2} + k^{2} v_{2}^{2}} = \sqrt{k^{2} (v_{1}^{2} + v_{2}^{2})} = |k| \,\sqrt{v_{1}^{2} + v_{2}^{2}} = |k| \,\norm{\textbf{v}}\). So \(k\textbf{v}\) and \((kv_{1}, kv_{2})\) have the same magnitude and direction. This proves (a).
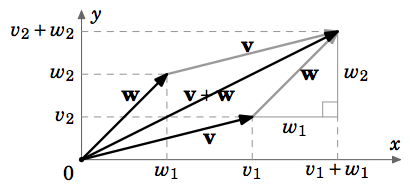
(b) Without loss of generality, we assume that \(v_{1}, v_{2}, w_{1}, w_{2} > 0\) (the other possibilities are handled in a similar manner). From Figure 1.2.5, we see that when translating \(\textbf{w}\) to start at the end of \(\textbf{v}\), the new terminal point of \(\textbf{w}\) is \((v_{1} + w_{1}, v_{2} + w_{2})\), so by the definition of \(\textbf{v} + \textbf{w}\) this must be the terminal point of \(\textbf{v} + \textbf{w}\). This proves (b).
Theorem 1.4
Let \(\textbf{v} = (v_{1}, v_{2}, v_{3})\), \(\textbf{w} = (w_{1}, w_{2}, w_{3})\) be vectors in \(\mathbb{R}^{3}\), let \(k\) be a scalar. Then
- \(k\textbf{v} = (kv_{1}, kv_{2}, kv_{3})\)
- \(\textbf{v + w} = (v_{1} + w_{1}, v_{2} + w_{2}, v_{3} + w_{3})\)
The following theorem summarizes the basic laws of vector algebra.
Theorem 1.5
For any vectors \(\textbf{u}, \textbf{v}, \textbf{w}\), and scalars \(k, l\),
we have
- \(\textbf{v} + \textbf{w} = \textbf{w} + \textbf{v}\) Commutative Law
- \(\textbf{u} + (\textbf{v} + \textbf{w}) = (\textbf{u} + \textbf{v}) + \textbf{w}\) Associative Law
- \(\textbf{v} + \textbf{0} = \textbf{v} = \textbf{0} + \textbf{v}\) Additive Identity
- \(\textbf{v} + (-\textbf{v}) = \textbf{0}\) Additive Inverse
- \(k(l\textbf{v}) = (kl)\textbf{v}\) Associative Law
- \(k(\textbf{v} + \textbf{w}) = k\textbf{v} + k\textbf{w}\) Distributive Law
- \((k + l)\textbf{v} = k\textbf{v} + l\textbf{v}\) Distributive Law
(a) We already presented a geometric proof of this in Figure 1.2.4 (a).
(b) To illustrate the difference between analytic proofs and geometric proofs in vector algebra, we will present both types here. For the analytic proof, we will use vectors in \(\mathbb{R}^{3}\) (the proof for \(\mathbb{R}^{2}\) is similar).
Let \(\textbf{u} = (u_{1}, u_{2}, u_{3})\), \(\textbf{v} = (v_{1}, v_{2}, v_{3})\), \(\textbf{w} = (w_{1}, w_{2}, w_{3})\) be vectors in \(\mathbb{R}^{3}\). Then
\[\nonumber \begin{split}\textbf{u} + (\textbf{v} + \textbf{w}) &= (u_{1}, u_{2}, u_{3}) + ((v_{1}, v_{2}, v_{3}) + (w_{1}, w_{2}, w_{3})) \\[4pt] &= (u_{1}, u_{2}, u_{3}) + (v_{1} + w_{1}, v_{2} + w_{2}, v_{3} + w_{3}) \qquad \qquad &&\text{by Theorem 1.4 (b)} \\[4pt] &= (u_{1} + (v_{1} + w_{1}), u_{2} + (v_{2} + w_{2}), u_{3} + (v_{3} + w_{3})) &&\text{by Theorem 1.4 (b)} \\[4pt] &= ((u_{1} + v_{1}) + w_{1}, (u_{2} + v_{2}) + w_{2}, (u_{3} + v_{3}) + w_{3}) &&\text{by properties of real numbers} \\[4pt] &= (u_{1} + v_{1}, u_{2} + v_{2}, u_{3} + v_{3}) + (w_{1}, w_{2}, w_{3}) &&\text{by Theorem 1.4 (b)} \\[4pt] &= (\textbf{u} + \textbf{v}) + \textbf{w} \\[4pt] \end{split}\]
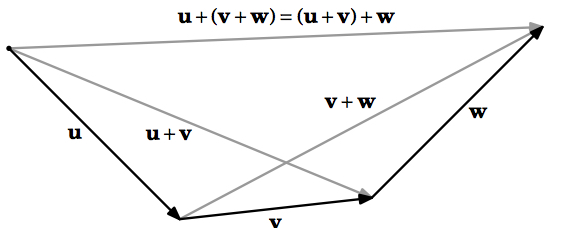
This completes the analytic proof of (b). Figure 1.2.6 provides the geometric proof.
(c) We already discussed this on p.10.
(d) We already discussed this on p.10.
(e) We will prove this for a vector \(\textbf{v} = (v_{1}, v_{2}, v_{3})\) in \(\mathbb{R}^{3}\) (the proof for \(\mathbb{R}^{2}\) is similar):
\[\nonumber \begin{split} k(l\textbf{v}) &= k(lv_{1}, lv_{2}, lv_{3}) \qquad & \text{by Theorem 1.4 (a)} \\[4pt] &= (klv_{1}, klv_{2}, klv_{3}) & \text{by Theorem 1.4 (a)} \\[4pt] &= (kl)(v_{1}, v_{2}, v_{3}) & \text{by Theorem 1.4 (a)} \\[4pt] &= (kl)\textbf{v} \\[4pt] \end{split}\]
(f) and (g): Left as exercises for the reader.
A \(\textbf{unit vector}\) is a vector with magnitude 1. Notice that for any nonzero vector \(\textbf{v}\), the vector \(\frac{\textbf{v}}{\norm{\textbf{v}}}\) is a unit vector which points in the same direction as \(\textbf{v}\), since \(\frac{1}{\norm{\textbf{v}}} > 0\) and
\(\norm{\frac{\textbf{v}}{\norm{\textbf{v}}}} = \frac{\norm{\textbf{v}}}{\norm{\textbf{v}}} = 1\). Dividing a nonzero vector \(\textbf{v}\) by \(\norm{\textbf{v}}\) is often called \(\textit{normalizing}\) \(\textbf{v}\).
There are specific unit vectors which we will often use, called the \(\textbf{basis vectors}\): \(\textbf{i} = (1,0,0)\), \(\textbf{j} = (0,1,0)\), and \(\textbf{k} = (0,0,1)\) in \(\mathbb{R}^{3}\); \(\textbf{i} = (1,0)\) and \(\textbf{j} = (0,1)\) in \(\mathbb{R}^{2}\). These are useful for several reasons: they are mutually perpendicular, since they lie on distinct coordinate axes; they are all unit vectors: \(\norm{\textbf{i}} = \norm{\textbf{j}} = \norm{\textbf{k}} = 1\); every vector can be written as a unique scalar combination of the basis vectors: \(\textbf{v} = (a,b) = a\,\textbf{i} + b\,\textbf{j}\) in \(\mathbb{R}^{2}\), \(\textbf{v} = (a,b,c) = a\,\textbf{i} + b\,\textbf{j} + c\,\textbf{k}\) in \(\mathbb{R}^{3}\). See Figure 1.2.7.
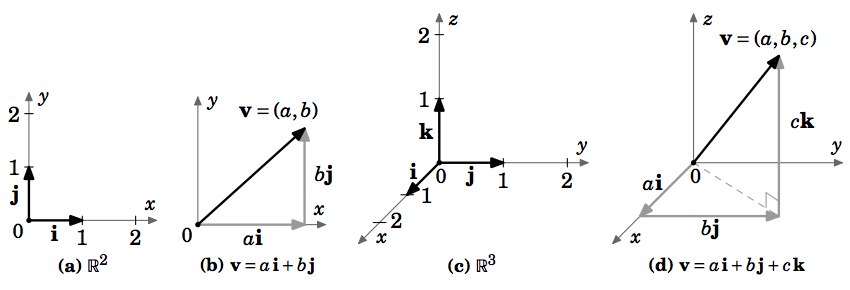
When a vector \(\textbf{v} = (a,b,c)\) is written as \(\textbf{v} = a\,\textbf{i} + b\,\textbf{j} + c\,\textbf{k}\), we say that \(\textbf{v}\) is in \(\textit{component form}\), and that \(a\), \(b\), and \(c\) are the \(\textbf{i}\), \(\textbf{j}\), and \(\textbf{k}\) components, respectively, of \(\textbf{v}\). We have:
\begin{align*}
\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}, k \text{ a scalar} &\Longrightarrow k\textbf{v} = kv_{1}\textbf{i} + kv_{2}\textbf{j} + kv_{3}\textbf{k}\\[4pt]
\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}, \textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k} &\Longrightarrow \textbf{v} + \textbf{w} =
(v_{1}w_{1})\textbf{i} + (v_{2}w_{2})\textbf{j} + (v_{3}w_{3})\textbf{k}\\[4pt]
\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k} &\Longrightarrow \norm{\textbf{v}} =
\sqrt{v_{1}^{2} + v_{2}^{2} + v_{3}^{2}}
\end{align*}
Example 1.4
Let \(\textbf{v} = (2,1,-1)\) and \(\textbf{w} = (3,-4,2)\) in \(\mathbb{R}^{3}\).
- Find \(\textbf{v} - \textbf{w}\).
\(\textit{Solution:}\) \(\textbf{v} - \textbf{w} = (2 - 3,1 - (-4), -1 - 2) = (-1,5,-3)\) - Find \(3\textbf{v} + 2\textbf{w}\).
\(\textit{Solution:}\) \(3\textbf{v} + 2\textbf{w} = (6,3,-3) + (6,-8,4) = (12,-5,1)\) - Write \(\textbf{v}\) and \(\textbf{w}\) in component form.
\(\textit{Solution:}\) \(\textbf{v} = 2\,\textbf{i} + \textbf{j} - \textbf{k}\), \(\textbf{w} = 3\,\textbf{i} - 4\,\textbf{j} + 2\,\textbf{k}\) - Find the vector \(\textbf{u}\) such that \(\textbf{u} + \textbf{v} = \textbf{w}\).
\(\textit{Solution:}\) By Theorem 1.5, \(\textbf{u} = \textbf{w} - \textbf{v} = -(\textbf{v} - \textbf{w}) = -(-1,5,-3) = (1,-5,3)\), by part(a). - Find the vector \(\textbf{u}\) such that \(\textbf{u} + \textbf{v} + \textbf{w} = \textbf{0}\).
\(\textit{Solution:}\) By Theorem 1.5, \(\textbf{u} = -\textbf{w} - \textbf{v} = -(3,-4,2) - (2,1,-1) = (-5,3,-1)\). - Find the vector \(\textbf{u}\) such that \(2\textbf{u} + \textbf{i} - 2\,\textbf{j} = \textbf{k}\).
\(\textit{Solution:}\) \(2\textbf{u} = -\textbf{i} + 2\,\textbf{j} + \textbf{k} \Longrightarrow \textbf{u} = -\frac{1}{2}\,\textbf{i} + \textbf{j} + \frac{1}{2}\,\textbf{k}\) - Find the unit vector \(\frac{\textbf{v}}{\norm{\textbf{v}}}\).
\(\textit{Solution:}\) \(\frac{\textbf{v}}{\norm{\textbf{v}}} = \frac{1}{\sqrt{2^{2} + 1^{2} + (-1)^{2}}} \,(2,1,-1) = \left(\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{-1}{\sqrt{6}}\right)\)
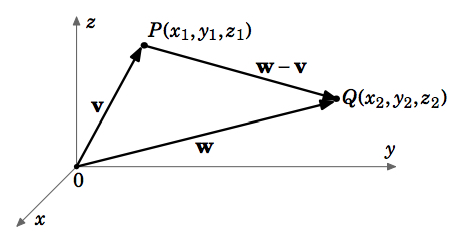
We can now easily prove Theorem 1.1 from the previous section. The distance \(d\) between two points \(P = (x_{1}, y_{1}, z_{1})\) and \(Q = (x_{2}, y_{2}, z_{2})\) in \(\mathbb{R}^{3}\) is the same as the length of the vector \(\textbf{w} - \textbf{v}\), where the vectors \(\textbf{v}\) and \(\textbf{w}\) are defined as \(\textbf{v} = (x_{1}, y_{1}, z_{1})\) and \(\textbf{w} = (x_{2}, y_{2}, z_{2})\) (see Figure 1.2.8). So since \(\textbf{w} - \textbf{v} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})\), then \(d = \norm{\textbf{w} - \textbf{v}} = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + (z_{2} - z_{1})^{2}}\) by Theorem 1.2.