1.5: Lines and Planes
- Page ID
- 2216
Now that we know how to perform some operations on vectors, we can start to deal with some familiar geometric objects, like lines and planes, in the language of vectors. The reason for doing this is simple: using vectors makes it easier to study objects in 3-dimensional Euclidean space. We will first consider lines.
Line through a point, parallel to a vector
Let \(P=(x_0,y_0,z_0)\) be a point in \(R3\), let \(v=(a,b,c)\) be a nonzero vector, and let \(L\) be the line through \(P\) which is parallel to \(v\) (see Figure 1.5.1).
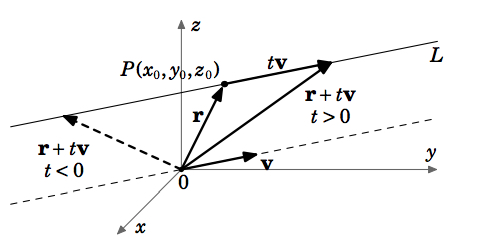
Let \(\textbf{r}=(x_0,y_0,z_0)\) be the vector pointing from the origin to P. Since multiplying the vector \(\textbf{v}\) by a scalar \(t\) lengthens or shrinks \(\textbf{v}\) while preserving its direction if \(t>0\), and reversing its direction if \(t<0\), then we see from Figure 1.5.1 that every point on the line \(L\) can be obtained by adding the vector \(t \textbf{v}\) to the vector \(\textbf{r}\) for some scalar \(t\). That is, as \(t\) varies over all real numbers, the vector \(\textbf{r} + t \textbf{v}\) will point to every point on \(L\). We can summarize the \(\textit{vector representation of \(L\)}\) as follows:
For a point \(P = (x_{0}, y_{0}, z_{0})\) and nonzero vector \(\textbf{v}\) in \(\mathbb{R}^{3}\), the line \(L\) through \(P\) parallel to \(\textbf{v}\) is given by
\[\textbf{r} + t \textbf{v}, \text{for} -\infty < t < \infty \label{Eq1.16}\]
where \(\textbf{r} = (x_{0}, y_{0}, z_{0})\) is the vector pointing to \(P\).
Note that we used the correspondence between a vector and its terminal point. Since \(\textbf{v} = (a,b,c)\), then the terminal point of the vector \(\textbf{r} + t \textbf{v}\) is \((x_{0} + at, y_{0} + bt, z_{0} + ct)\). We then get the \(\textit{parametric representation of L}\) with the \(\textit{parameter}\) \(t\):
For a point \(P = (x_{0}, y_{0}, z_{0})\) and nonzero vector \(\textbf{v} = (a,b,c)\) in \(\mathbb{R}^{3}\), the line \(L\) through \(P\) parallel to \(\textbf{v}\) consists of all points \((x,y,z)\) given by
\[x = x_{0} + at,\quad y = y_{0} + bt,\quad z = z_{0} + ct, \text{for} -\infty < t < \infty \label{Eq1.17}\]
Note that in both representations we get the point \(P\) on \(L\) by letting \(t = 0\).
In Equation \ref{Eq1.17}, if \(a \ne 0\), then we can solve for the parameter \(t\): \(t = (x - x_{0})/a\). We can also solve for \(t\) in terms of \(y\) and in terms of \(z\) if neither \(b\) nor \(c\), respectively, is zero: \(t = (y - y_{0})/b\) and \(t = (z - z_{0})/c\). These three values all equal the same value \(t\), so we can write the following system of equalities, called the \(\textit{symmetric representation of L}\):
For a point \(P = (x_{0}, y_{0}, z_{0})\) and vector \(\textbf{v} = (a,b,c)\) in \(\mathbb{R}^{3}\) with \(a\), \(b\) and \(c\) all nonzero, the line \(L\) through \(P\) parallel to \(\textbf{v}\) consists of all points \((x,y,z)\) given by the equations
\[\frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c}\]
You may have noticed that the vector representation of \(L\) in Equation \ref{Eq1.16} is more compact than the parametric and symmetric formulas. That is an advantage of using vector notation. Technically, though, the vector representation gives us the \(\textit{vectors}\) whose terminal points make up the line \(L\), not just \(L\) itself. So you have to remember to identify the vectors \(\textbf{r} + t \textbf{v}\) with their terminal points. On the other hand, the parametric representation \(\textit{always}\) gives just the points on \(L\) and nothing else.
Solution
(a) Let \(\textbf{r} = (2,3,5)\). Then by Equation \ref{Eq1.16}, \(L\) is given by: \[\nonumber \textbf{r} + t \textbf{v} = (2,3,5) + t(4,-1,6), \text{for} -\infty < t < \infty\]
(b) \(L\) consists of the points \((x,y,z)\) such that \[\nonumber x = 2 + 4t, y = 3 - t, z = 5 + 6t, \text{for} -\infty < t < \infty\]
(c) \(L\) consists of the points \((x,y,z)\) such that \[\nonumber \frac{x - 2}{4} = \frac{y - 3}{-1} = \frac{z - 5}{6}\]
(d) Letting \(t=1\) and \(t=2\) in part(b) yields the points \((6,2,11)\) and \((10,1,17)\) on \(L\).
Line through two points
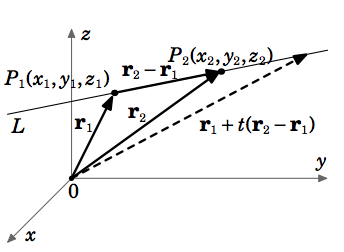
Let \(P_{1} = (x_{1}, y_{1}, z_{1})\), \(P_{2} = (x_{2}, y_{2}, z_{2})\) be distinct points in \(\mathbb{R}^{3}\), and let \(\textbf{r}_{1} = (x_{1}, y_{1}, z_{1})\), \(\textbf{r}_{2} = (x_{2}, y_{2}, z_{2})\). Then the line \(L\) through \(P_{1}\) and \(P_{2}\) has the following representations:
\(\textit{Vector:}\) \[\textbf{r}_{1} + t(\textbf{r}_{2} - \textbf{r}_{1}) \text{, for} -\infty < t < \infty\]
\(\textit{Parametric:}\) \[x = x_{1} + (x_{2} - x_{1})t, y = y_{1} + (y_{2} - y_{1})t, z = z_{1} + (z_{2} - z_{1})t, \text{for} -\infty < t < \infty \label{Eq1.21}\]
\(\textit{Symmetric:}\) \[\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}} \text{if \(x_{1} \ne x_{2}\), \(y_{1} \ne y_{2}\), and \(z_{1} \ne z_{2}\)}\]
Solution
By Equation \ref{Eq1.21}, \(L\) consists of the points \((x,y,z)\) such that \[\nonumber x = -3 + 7t, y = 1 +3t, z = -4 -2t, \text{for} -\infty < t < \infty\]
Distance between a point and a line
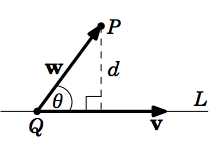
\[d = \frac{\norm{\textbf{v} \times \textbf{w}}}{\norm{\textbf{v}}}\]
Find the distance \(d\) from the point \(P = (1,1,1)\) to the line \(L\) in Example 1.20.
Solution
From Example 1.20, we see that we can represent \(L\) in vector form as: \(\textbf{r} + t \textbf{v}\), for \(\textbf{r} = (-3,1,-4)\) and \(\textbf{v} = (7,3,-2)\). Since the point \(Q = (-3,1,-4)\) is on \(L\), then for \(\textbf{w} = \overrightarrow{QP} = (1,1,1) - (-3,1,-4) = (4,0,5)\), we have:
\[\nonumber \textbf{v} \times \textbf{w} = \left|\begin{array}{rrr}\textbf{i} & \textbf{j} & \textbf{k}\\[4pt]7 & 3 & -2\\[4pt]
4 & 0 & 5\end{array}\right|
= \left|\begin{array}{rr}3 & -2\\[4pt]0 & 5\end{array}\right| \textbf{i} \;-\;
\left|\begin{array}{rr}7 & -2\\[4pt]4 & 5\end{array}\right| \textbf{j} \;+\;
\left|\begin{array}{rr}7 & 3\\[4pt]4 & 0\end{array}\right| \textbf{k}
= 15\,\textbf{i} - 43\,\textbf{j} - 12\,\textbf{k} \text{ , so}\\[4pt] \nonumber
d = \frac{\norm{\textbf{v} \times \textbf{w}}}{\norm{\textbf{v}}} =
\frac{\norm{15\,\textbf{i} - 43\,\textbf{j} - 12\,\textbf{k}}}{\norm{(7,3,-2)}}
= \frac{\sqrt{15^{2} + (-43)^{2} + (-12)^{2}}}{\sqrt{7^{2} + 3^{2} + (-2)^{2}}}
= \frac{\sqrt{2218}}{\sqrt{62}} = 5.98\]
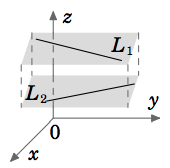
To determine whether two lines in \(\mathbb{R}^{3}\) intersect, it is often easier to use the parametric representation of the lines. In this case, you should use different parameter variables (usually \(s\) and \(t\)) for the lines, since the values of the parameters may not be the same at the point of intersection. Setting the two \((x,y,z)\) triples equal will result in a system of 3 equations in 2 unknowns (\(s\) and \(t\)).
Example 1.22
Find the point of intersection (if any) of the following lines: \[\nonumber \frac{x + 1}{3} = \frac{y - 2}{2} = \frac{z - 1}{-1} \text{ and } x + 3 = \frac{y - 8}{-3} = \frac{z + 3}{2}\]
Solution
First we write the lines in parametric form, with parameters \(s\) and \(t\):
\[\nonumber x = -1 + 3s, y = 2 + 2s, z = 1 - s \text{ and } x = -3 + t, y = 8 - 3t, z = -3 + 2t\]
The lines intersect when \((-1 + 3s,2 + 2s,1 - s) = (-3 + t,8 - 3t,-3 + 2t)\) for some \(s\), \(t\):
\begin{align*}
\nonumber -1 + 3s = -3 + t &: \Rightarrow t = 2 + 3s\\[4pt] \nonumber
2 + 2s = 8 - 3t &: \Rightarrow 2 + 2s = 8 - 3(2 + 3s) = 2 - 9s \Rightarrow 2s = -9s \Rightarrow s = 0 \Rightarrow t = 2 + 3(0) = 2\\[4pt] \nonumber
1 - s = -3 + 2t &: 1 - 0 = -3 + 2(2) \Rightarrow 1 = 1 \checkmark \text{(Note that we had to check this.)}
\end{align*}
Letting \(s = 0\) in the equations for the first line, or letting \(t = 2\) in the equations for the second line, gives the point of intersection \((-1,2,1)\).
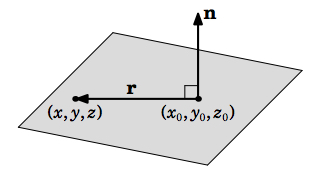
Conversely, if \((x,y,z)\) is any point in \(\mathbb{R}^{3}\) such that \(\textbf{r} = (x - x_{0}, y - y_{0}, z - z_{0}) \ne \textbf{0}\) and \(\textbf{n} \cdot \textbf{r} = 0\), then \(\textbf{r} \perp \textbf{n}\) and so \((x,y,z)\) lies in \(P\). This proves the following theorem:
Theorem 1.18
Let \(P\) be a plane in \(\mathbb{R}^{3}\), let \((x_{0}, y_{0}, z_{0})\) be a point in \(P\), and let \(\textbf{n} = (a,b,c)\) be a nonzero vector which is perpendicular to \(P\). Then \(P\) consists of the points \((x,y,z)\) satisfying the vector equation:
\[\textbf{n} \cdot \textbf{r} = 0\]
where \(\textbf{r} = (x - x_{0}, y - y_{0}, z - z_{0})\), or equivalently:
\[a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0 \label{Eq1.25}\]
The above equation is called the \(\textbf{point-normal form}\) of the plane \(P\).
Solution
By Equation \ref{Eq1.25}, the plane \(P\) consists of all points \((x,y,z)\) such that:
\[\nonumber 2(x + 3) + 4(y - 1) + 8(z - 3) = 0 \]
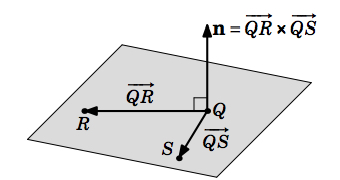
Solution
Let \(Q = (2,1,3)\), \(R = (1,-1,2)\) and \(S = (3,2,1)\). Then for the vectors \(\overrightarrow{QR} = (-1,-2,-1)\) and \(\overrightarrow{QS} = (1,1,-2)\), the plane \(P\) has a normal vector
\[\nonumber \textbf{n} = \overrightarrow{QR} \times \overrightarrow{QS} = (-1,-2,-1) \times (1,1,-2) = (5,-3,1)\]
So using Equation \ref{Eq1.25} with the point \(Q\) (we could also use \(R\) or \(S\)), the plane \(P\) consists of all points \((x,y,z)\) such that:
\[\nonumber 5(x - 2) - 3(y - 1) + (z - 3) = 0\]
or in normal form,
\[\nonumber 5x - 3y + z - 10 = 0\]
We mentioned earlier that skew lines in \(\mathbb{R}^{3}\) lie on separate, parallel planes. So two skew lines do not determine a plane. But two (nonidentical) lines which either intersect or are parallel do determine a plane. In both cases, to find the equation of the plane that contains those two lines, simply pick from the two lines a total of three noncollinear points (i.e. one point from one line and two points from the other), then use the technique above, as in Example 1.24, to write the equation. We will leave examples of this as exercises for the reader.
Distance between a point and a plane
The distance between a point in \(\mathbb{R}^{3}\) and a plane is the length of the line segment from that point to the plane which is perpendicular to the plane. The following theorem gives a formula for that distance.
Theorem 1.19
Let \(Q = (x_{0}, y_{0}, z_{0})\) be a point in \(\mathbb{R}^{3}\), and let \(P\) be a plane with normal form \(ax + by + cz + d = 0\) that does not contain \(Q\). Then the distance \(D\) from \(Q\) to \(P\) is:
\[D = \frac{|ax_{0} + by_{0} + cz_{0} + d|}{\sqrt{a^{2} + b^{2} + c^{2}}}\]
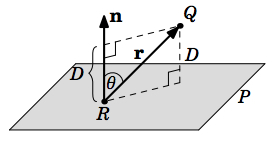
By Theorem 1.6 in Section 1.3, we know that \(\cos \theta = \dfrac{\textbf{n} \cdot \textbf{r}}{\norm{\textbf{n}} \norm{\textbf{r}}}\), so
\[\nonumber \begin{align}D &= |\cos \theta|\,\norm{\textbf{r}}= \dfrac{|\textbf{n} \cdot \textbf{r}|}{\norm{\textbf{n}} \norm{\textbf{r}}}\,\norm{\textbf{r}}= \dfrac{|\textbf{n} \cdot \textbf{r}|}{\norm{\textbf{n}}}= \dfrac{|a(x_{0} - x) + b(y_{0} - y) + c(z_{0} - z)|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\[4pt] \nonumber &= \dfrac{ax_{0} + by_{0} + cz_{0} - (ax + by + cz)}{\sqrt{a^{2} + b^{2} + c^{2}}}= \dfrac{|ax_{0} + by_{0} + cz_{0} - (-d)|}{\sqrt{a^{2} + b^{2} + c^{2}}}= \dfrac{|ax_{0} + by_{0} + cz_{0} + d|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\[4pt] \end{align}\]
If \(\textbf{n}\) points away from the side of \(P\) where the point \(Q\) is located, then \(90^{\circ} < \theta < 180^{\circ}\) and so \(\cos \theta < 0\). The distance \(D\) is then \(|\cos \theta| \, \norm{\textbf{r}}\), and thus repeating the same argument as above still gives the same result.
\[\nonumber D = \frac{|5(2) - 3(4) + 1(-5) - 10|}{\sqrt{5^{2} + (-3)^{2} + 1^{2}}} = \frac{|-17|}{\sqrt{35}} = \frac{17}{\sqrt{35}} \approx 2.87\]
Line of intersection of two planes
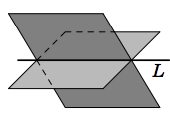
\[L: \textbf{r} + t(\textbf{n}_{1} \times \textbf{n}_{2}) \text{, for} -\infty < t < \infty\]
where \(\textbf{r}\) is any vector pointing to a point belonging to both planes. To find a point in both planes, find a common solution \((x,y,z)\) to the two normal form equations of the planes. This can often be made easier by setting one of the coordinate variables to zero, which leaves you to solve two equations in just two unknowns.
\[\nonumber \begin{align} -&3y + z - 10 = 0 \\[4pt] \nonumber &4y - z + 3 = 0 \\[4pt] \end{align}\]
The second equation gives \(z = 4y + 3\), substituting that into the first equation gives \(y = 7\). Then \(z = 31\), and so the point \((0,7,31)\) is on \(L\). Since \(\textbf{n}_{1} \times \textbf{n}_{2} = (-1,7,26)\), then \(L\) is given by:
\[\nonumber \textbf{r} + t(\textbf{n}_{1} \times \textbf{n}_{2}) = (0,7,31) + t(-1,7,26), \text{for} -\infty < t < \infty\]
or in parametric form:
\[\nonumber x = -t, y = 7 + 7t, z = 31 +26t, \text{for} -\infty < t < \infty\]


