2.1: Functions of Two or Three Variables
- Page ID
- 2250
In Section 1.8 we discussed vector-valued functions of a single real variable. We will now examine real-valued functions of a point (or vector) in \(\mathbb{R}^2\) or \(\mathbb{R}^ 3\). For the most part these functions will be defined on sets of points in \(\mathbb{R}^2\), but there will be times when we will use points in \(\mathbb{R}^ 3\), and there will also be times when it will be convenient to think of the points as vectors (or terminal points of vectors).
A real-valued function f defined on a subset \(D\) of \(\mathbb{R}^2\) is a rule that assigns to each point \(f(x,y)\) in \(D\) a real number \(f(x,y)\). The largest possible set \(D\) in \(\mathbb{R}^2\) on which \(f\) is defined is called the domain of \(f\), and the range of \(f\) is the set of all real numbers \(f(x,y)\) as \((x,y)\) varies over the domain \(D\). A similar definition holds for functions \(f(x,y,z)\) defined on points \((x,y,z)\) in \(\mathbb{R}^ 3\).
Example 2.1
The domain of the function
\[\nonumber f(x,y)=xy\]
is all the \(\mathbb{R}^2\), and the range of \(f\) is all of \(\mathbb{R}\).
Example 2.2
The domain of the function
\[\nonumber f(x,y)=\dfrac{1}{x-y}\]
is all of \(\mathbb{R}^2\) except the points \((x,y)\) for which \(x = y\). That is, the domain is the set \(D = \{(x, y) : x \ne y\}\). The range of \(f\) is all real numbers except 0.
Example 2.3
The domain of the function
\[\nonumber f(x,y)=\sqrt{1-x^2-y^2}\]
is the set \(D = \{(x, y) : x^ 2 + y^ 2 ≤ 1\}\), since the quantity inside the square root is nonnegative if and only if 1−\((x^2 + y^2 ) ≥ 0\). We see that \(D\) consists of all points on and inside the unit circle in \(\mathbb{R}^2\) (\(D\) is sometimes called the closed unit disk). The range of \(f\) is the interval [0,1] in \(\mathbb{R}\).
Example 2.4
The domain of the function
\[\nonumber f(x,y,z)=e^{x+y-z}\]
is all of \(\mathbb{R}^ 3\), and the range of \(f\) is all positive real numbers.
A function \(f (x, y)\) defined in \(\mathbb{R}^2\) is often written as \(z = f (x, y)\), as was mentioned in Section 1.1, so that the graph of \(f (x, y)\) is the set \(\{(x, y, z) : z = f (x, y)\}\) in \(\mathbb{R}^3\). So we see that this graph is a surface in \(\mathbb{R}^3\), since it satisfies an equation of the form \(F(x, y, z) = 0\) (namely, F(x, y, z) = f (x, y) − z). The traces of this surface in the planes \(z = c\), where \(c\) varies over \(\mathbb{R}\), are called the level curves of the function. Equivalently, the level curves are the solution sets of the equations \(f (x, y) = c\), for \(c\) in \(\mathbb{R}\). Level curves are often projected onto the \(xy\)-plane to give an idea of the various “elevation” levels of the surface (as is done in topography).
Example 2.5
The graph of the function
\[\nonumber f(x,y)=\dfrac{\sin \sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}\]
is shown below. Note that the level curves (shown both on the surface and projected onto the \(xy\)-plane) are groups of concentric circles.
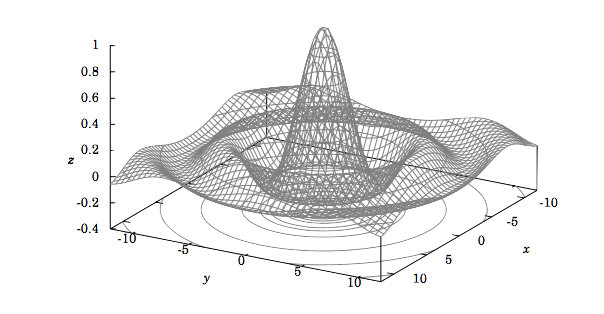
You may be wondering what happens to the function in Example 2.5 at the point \((x, y) = (0,0)\), since both the numerator and denominator are 0 at that point. The function is not defined at (0,0), but the limit of the function exists (and equals 1) as \((x, y)\) approaches (0,0). We will now state explicitly what is meant by the limit of a function of two variables.
Definition 2.1
Let \((a,b)\) be a point in \(\mathbb{R}^2\), and let \(f(x,y)\) be a real-valued function defined on some set containing \((a,b)\) (but not necessarily defined at \((a,b)\) itself). Then we say that the limit of \(f(x,y)\) equals \(L\) as \((x,y)\) approaches \((a,b)\), written as
\[\label{Eq2.1} \lim \limits_{(x,y) \to (a,b)}f(x,y)=L\]
if given any \(\epsilon > 0\), there exists a \(δ > 0\) such that
\[\nonumber \lvert f(x,y)-L\rvert<\epsilon \text{ whenever } 0<\sqrt{(x-a)^2+(y-b)^2}<δ\]
A similar definition can be made for functions of three variables. The idea behind the above definition is that the values of \(f(x, y)\) can get arbitrarily close to \(L\) (i.e. within \(\epsilon\) of \(L\)) if we pick \((x, y)\) sufficiently close to \((a,b)\) (i.e. inside a circle centered at \((a,b)\) with some sufficiently small radius δ).
If you recall the “epsilon-delta” proofs of limits of real-valued functions of a single variable, you may remember how awkward they can be, and how they can usually only be done easily for simple functions. In general, the multivariable cases are at least equally awkward to go through, so we will not bother with such proofs. Instead, we will simply state that when the function \(f (x, y)\) is given by a single formula and is defined at the point \((a,b)\) (e.g. is not some indeterminate form like 0/0) then you can just substitute \((x, y) = (a,b)\) into the formula for \(f (x, y)\) to find the limit.
Example 2.6
\[\nonumber \lim \limits_{(x,y) \to (1,2)} \dfrac{xy}{x^2+y^2}=\dfrac{(1)(2)}{1^2+2^2}=\dfrac{2}{5}\]
since \(f(x,y)=\dfrac{xy}{x^2+y^2}\) is properly defined at the point (1,2).
The major difference between limits in one variable and limits in two or more variables has to do with how a point is approached. In the single-variable case, the statement \(“x → a”\) means that \(x\) gets closer to the value a from two possible directions along the real number line (see Figure 2.1.2(a)). In two dimensions, however, \((x, y)\) can approach a point \((a,b)\) along an infinite number of paths (see Figure 2.1.2(b)).
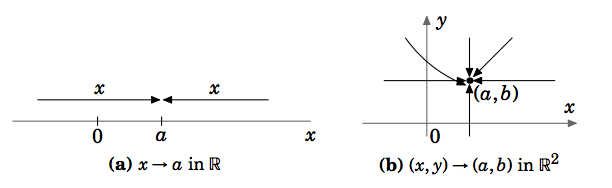
Example 2.7
\[\nonumber \lim \limits_{(x,y) \to (0,0)} \dfrac{xy}{x^2+y^2} \text{ does not exist}\]
Note that we can not simply substitute \((x, y) = (0,0)\) into the function, since doing so gives an indeterminate form 0/0. To show that the limit does not exist, we will show that the function approaches different values as \((x, y) \)approaches (0,0) along different paths in \(\mathbb{R}^2\). To see this, suppose that \((x, y) → (0,0)\) along the positive \(x\)-axis, so that \(y = 0\) along that path. Then
\[\nonumber f(x,y)=\dfrac{xy}{x^2+y^2}=\dfrac{x0}{x^2+0^2}=0\]
along that path (since \(x > 0\) in the denominator). But if \((x, y) → (0,0)\) along the straight line \(y = x\) through the origin, for \(x > 0\), then we see that
\[\nonumber f(x,y)=\dfrac{xy}{x^2+y^2}=\dfrac{x^2}{x^2+y^2}=\dfrac{1}{2}\]
which means that \(f (x, y)\) approaches different values as \((x, y) → (0,0) \)along different paths. Hence the limit does not exist.
Limits of real-valued multivariable functions obey the same algebraic rules as in the single-variable case, as shown in the following theorem, which we state without proof.
Theorem 2.1
Suppose that \(\lim \limits_{(x,y) \to (a,b)}f(x,y)\) and \(\lim \limits_{(x,y) \to (a,b)}g(x,y)\) both exist, and that \(k\) is some scalar. Then:
- \(\lim \limits_{(x,y) \to (a,b)}\left [ f(x,y)\pm g(x,y)\right ] = \left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \pm \left [ \lim \limits_{(x,y) \to (a,b)}g(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}kf(x,y)=k\left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}\left [ f(x,y)g(x,y)\right ] =\left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \left [ \lim \limits_{(x,y) \to (a,b)}g(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{\lim \limits_{(x,y) \to (a,b)}f(x,y)}{\lim \limits_{(x,y) \to (a,b)}g(x,y)}\) if \(\lim \limits_{(x,y) \to (a,b)}g(x,y)\ne 0\)
- If \(\lvert f(x,y)-L\rvert \le g(x,y)\) for all \((x,y)\) and if \(\lim \limits_{(x,y) \to (a,b)}g(x,y)=0\), then \(\lim \limits_{(x,y) \to (a,b)}f(x,y)=L\)
Note that in part (e), it suffices to have \(\lvert f(x,y)-L\rvert \le g(x,y)\) for all \((x, y)\) “sufficiently close” to \((a,b)\) (but excluding \((a,b)\) itself).
Example 2.8
Show that
\[\nonumber \lim \limits_{(x,y) \to (0,0)}\dfrac{y^4}{x^2+y^2}=0\]
Since substituting \((x, y) = (0,0)\) into the function gives the indeterminate form 0/0, we need an alternate method for evaluating this limit. We will use Theorem 2.1(e). First, notice that \(y^4 = (\sqrt{y^2})^4\) and so \(0\le y^4\le (\sqrt{x^2+y^2})^4\) for all \((x, y)\). But \((\sqrt{x^2+y^2})^4=(x^2+y^2)^2\). Thus, for all \((x, y) \neq (0,0)\) we have
\[\nonumber \lvert \dfrac{y^4}{x^2+y^2}\rvert \le \dfrac{(x^2+y^2)^2}{x^2+y^2}=x^2+y^2 → 0\,as\,(x,y)→(0,0)\]
Therefore \(\lim \limits_{(x,y) \to (0,0)}\dfrac{y^4}{x^2+y^2}=0\).
Continuity can be defined similarly as in the single-variable case.
Definition 2.2
A real-valued function \(f (x, y)\) with domain \(D\) in \(\mathbb{R}^2\) is continuous at the point \((a,b)\) in \(D\) if \(\lim \limits_{(x,y) \to (a,b)}f(x,y)=f(a,b)\). We say that \(f (x, y)\) is a continuous function if it is continuous at every point in its domain \(D\).
Unless indicated otherwise, you can assume that all the functions we deal with are continuous. In fact, we can modify the function from Example 2.8 so that it is continuous on all of \(\mathbb{R}^2\).
Example 2.9
Define a function \(f (x, y)\) on all of \(\mathbb{R}^2\) as follows:
\[\nonumber f(x,y)\cases{0 & \text{if } (x,y)=(0,0) \\[4pt] \nonumber \dfrac{y^4}{x^2+y^2} & \text{ if } (x,y)\neq (0,0) \\[4pt] }\]
Then \(f (x, y)\) is well-defined for all \((x, y)\) in \(\mathbb{R}^2\) (i.e. there are no indeterminate forms for any \((x, y))\), and we see that
\[\nonumber \lim \limits_{(x,y) \to (a,b)} f(x,y)=\dfrac{b^4}{a^2+b^2}=f(a,b) \text{ for } (a,b) \neq (0,0)\]
So since
\[\nonumber \lim \limits_{(x,y) \to (0,0)} f(x,y)=0=f(0,0) \text{ by Example 2.8, }\]
then \(f(x,y)\) is continuous on all of \(\mathbb{R}^2\).


