16.7E: Exercises for Section 16.7
- Page ID
- 66965
In exercises 1 - 6, without using Stokes’ theorem, calculate directly both the flux of \(curl \, \vecs F \cdot \vecs N\) over the given surface and the circulation integral around its boundary, assuming all are oriented clockwise.
1. \(\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + z^2\,\mathbf{\hat j} + x^2\,\mathbf{\hat k}\); \(S\) is the first-octant portion of plane \(x + y + z = 1\).
2. \(\vecs F(x,y,z) = z\,\mathbf{\hat i} + x\,\mathbf{\hat j} + y\,\mathbf{\hat k}\); \(S\) is hemisphere \(z = (a^2 - x^2 - y^2)^{1/2}\).
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = \pi a^2\)
3. \(\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 5\,\mathbf{\hat k}\); \(S\) is hemisphere \(z = (4 - x^2 - y^2)^{1/2}\).
4. \(\vecs F(x,y,z) = z\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 3y\,\mathbf{\hat k}\); \(S\) is upper hemisphere \(z = \sqrt{9 - x^2 - y^2}\).
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 18 \pi\)
5. \(\vecs F(x,y,z) = (x + 2z)\,\mathbf{\hat i} + (y - x)\,\mathbf{\hat j} + (z - y)\,\mathbf{\hat k}\); \(S\) is a triangular region with vertices \((3, 0, 0), \, (0, 3/2, 0),\) and \((0, 0, 3).\)
6. \(\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + 6z\,\mathbf{\hat j} + 3x\,\mathbf{\hat k}\); \(S\) is a portion of paraboloid \(z = 4 - x^2 - y^2\) and is above the \(xy\)-plane.
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = -8 \pi\)
In exercises 7 - 9, use Stokes’ theorem to evaluate \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS\) for the vector fields and surface.
7. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} - z\,\mathbf{\hat j}\) and \(S\) is the surface of the cube \(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\), except for the face where \(z = 0\) and using the outward unit normal vector.
8. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + x^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\); and \(C\) is the intersection of paraboloid \(z = x^2 + y^2\) and plane \(z = y\), and using the outward normal vector.
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 0\)
9. \(\vecs F(x,y,z) = 4y\,\mathbf{\hat i} + z \,\mathbf{\hat j} + 2y \,\mathbf{\hat k}\); and \(C\) is the intersection of sphere \(x^2 + y^2 + z^2 = 4\) with plane \(z = 0\), and using the outward normal vector.
10. Use Stokes’ theorem to evaluate \(\displaystyle \int_C \big[2xy^2z \, dx + 2x^2yz \, dy + (x^2y^2 - 2z) \, dz\big],\) where \(C\) is the curve given by \(x = \cos t, \, y = \sin t, \, 0 \leq t \leq 2\pi\), traversed in the direction of increasing \(t.\)
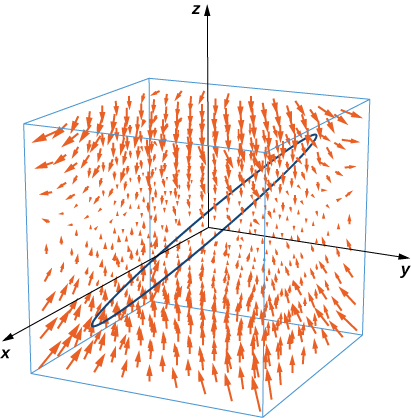
- Answer
- \(\displaystyle \int_C \vecs F \cdot dS = 0\)
11. [T] Use a computer algebraic system (CAS) and Stokes’ theorem to approximate line integral \(\displaystyle \int_C (y \, dx + z \, dy + x \, dz),\) where \(C\) is the intersection of plane \(x + y = 2\) and surface \(x^2 + y^2 + z^2 = 2(x + y)\), traversed counterclockwise viewed from the origin.
12. [T] Use a CAS and Stokes’ theorem to approximate line integral \(\displaystyle \int_C (3y\, dx + 2z \, dy - 5x \, dz),\) where \(C\) is the intersection of the \(xy\)-plane and hemisphere \(z = \sqrt{1 - x^2 - y^2}\), traversed counterclockwise viewed from the top—that is, from the positive \(z\)-axis toward the \(xy\)-plane.
- Answer
- \(\displaystyle \int_C \vecs F \cdot dS = - 9.4248\)
13. [T] Use a CAS and Stokes’ theorem to approximate line integral \(\displaystyle \int_C [(1 + y) \, z \, dx + (1 + z) x \, dy + (1 + x) y \, dz],\) where \(C\) is a triangle with vertices \((1,0,0), \, (0,1,0)\), and \((0,0,1)\) oriented counterclockwise.
14. Use Stokes’ theorem to evaluate \(\displaystyle \iint_S curl \, \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = e^{xy} cos \, z\,\mathbf{\hat i} + x^2 z\,\mathbf{\hat j} + xy\,\mathbf{\hat k}\), and \(S\) is half of sphere \(x = \sqrt{1 - y^2 - z^2}\), oriented out toward the positive \(x\)-axis.
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 0\)
15. [T] Use a CAS and Stokes’ theorem to evaluate \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS,\) where \(\vecs F(x,y,z) = x^2 y\,\mathbf{\hat i} + xy^2 \,\mathbf{\hat j} + z^3 \,\mathbf{\hat k}\) and \(C\) is the curve of the intersection of plane \(3x + 2y + z = 6\) and cylinder \(x^2 + y^2 = 4\), oriented clockwise when viewed from above.
16. [T] Use a CAS and Stokes’ theorem to evaluate \(\displaystyle \iint_S curl \, \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = \left( \sin(y + z) - yx^2 - \dfrac{y^3}{3}\right)\,\mathbf{\hat i} + x \, \cos (y + z) \,\mathbf{\hat j} + \cos (2y) \,\mathbf{\hat k}\) and \(S\) consists of the top and the four sides but not the bottom of the cube with vertices \((\pm 1, \, \pm1, \, \pm1)\), oriented outward.
- Answer
- \(\displaystyle \iint_S curl \, \vecs F \cdot dS = 2.6667\)
17. [T] Use a CAS and Stokes’ theorem to evaluate \(\displaystyle \iint_S curl \, \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + 3xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}\) and \(S\) is the top part of \(z = 5 - x^2 - y^2\) above plane \(z = 1\) and \(S\) is oriented upward.
18. Use Stokes’ theorem to evaluate \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,\) where \(\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + x\,\mathbf{\hat k}\) and \(S\) is a triangle with vertices \((1, 0, 0), \, (0, 1, 0)\) and \((0, 0, 1)\) with counterclockwise orientation.
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -\dfrac{1}{6}\)
19. Use Stokes’ theorem to evaluate line integral \(\displaystyle \int_C (z \, dx + x \, dy + y \, dz),\) where \(C\) is a triangle with vertices \((3, 0, 0), \, (0, 0, 2),\) and \((0, 6, 0)\) traversed in the given order.
20. Use Stokes’ theorem to evaluate \(\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right),\) where \(C\) is the curve of intersection of plane \(x + z = 1\) and ellipsoid \(x^2 + 2y^2 + z^2 = 1\), oriented clockwise from the origin.
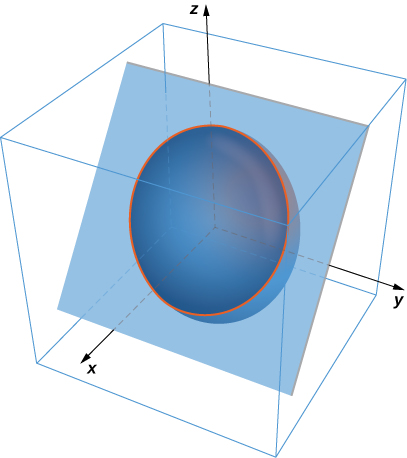
- Answer
- \(\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right) = - \dfrac{\pi}{4}\)
21. Use Stokes’ theorem to evaluate \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + ze^{xy}\,\mathbf{\hat k}\) and \(S\) is the part of surface \(z = 1 - x^2 - 2y^2\) with \(z \geq 0\), oriented counterclockwise.
22. Use Stokes’ theorem for vector field \(\vecs F(x,y,z) = z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 2z\,\mathbf{\hat k}\) where \(S\) is surface \(z = 1 - x^2 - 2y^2, \, z \geq 0\), \(C\) is boundary circle \(x^2 + y^2 = 1\), and \(S\) is oriented in the positive \(z\)-direction.
- Answer
- \(\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -3\pi\)
23. Use Stokes’ theorem for vector field \(\vecs F(x,y,z) = - \dfrac{3}{2} y^2\,\mathbf{\hat i} - 2 xy\,\mathbf{\hat j} + yz\,\mathbf{\hat k}\), where \(S\) is that part of the surface of plane \(x + y + z = 1\) contained within triangle \(C\) with vertices \((1, 0, 0), \, (0, 1, 0),\) and \((0, 0, 1),\) traversed counterclockwise as viewed from above.
24. A certain closed path \(C\) in plane \(2x + 2y + z = 1\) is known to project onto unit circle \(x^2 + y^2 = 1\) in the \(xy\)-plane. Let \(C\) be a constant and let \(\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\). Use Stokes’ theorem to evaluate \(\displaystyle \int_C(c \,\mathbf{\hat k} \times \vecs R) \cdot dS.\)
- Answer
- \(\displaystyle \int_C (c \,\mathbf{\hat k} \times \vecs R) \cdot dS = 2\pi c\)
25. Use Stokes’ theorem and let \(C\) be the boundary of surface \(z = x^2 + y^2\) with \(0 \leq x \leq 2\) and \(0 \leq y \leq 1\) oriented with upward facing normal. Define \(\vecs F(x,y,z) = \big(\sin (x^3) + xz\big) \,\mathbf{\hat i} + (x - yz)\,\mathbf{\hat j} + \cos (z^4) \,\mathbf{\hat k}\) and evaluate \(\int_C \vecs F \cdot dS\).
26. Let \(S\) be hemisphere \(x^2 + y^2 + z^2 = 4\) with \(z \geq 0\), oriented upward. Let \(\vecs F(x,y,z) = x^2 e^{yz}\,\mathbf{\hat i} + y^2 e^{xz} \,\mathbf{\hat j} + z^2 e^{xy}\,\mathbf{\hat k}\) be a vector field. Use Stokes’ theorem to evaluate \(\displaystyle \iint_S curl \, \vecs F \cdot dS.\)
- Answer
- \(\displaystyle \iint_S curl \, \vecs F \cdot dS = 0\)
27. Let \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + (e^{z^2} + y)\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}\) and let \(S\) be the graph of function \(y = \dfrac{x^2}{9} + \dfrac{z^2}{9} - 1\) with \(z \leq 0\) oriented so that the normal vector \(S\) has a positive y component. Use Stokes’ theorem to compute integral \(\displaystyle \iint_S curl \, \vecs F \cdot dS.\)
28. Use Stokes’ theorem to evaluate \(\displaystyle \oint \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = y\,\mathbf{\hat i} + z\,\mathbf{\hat j} + x\,\mathbf{\hat k}\) and \(C\) is a triangle with vertices \((0, 0, 0), \, (2, 0, 0)\) and \(0,-2,2)\) oriented counterclockwise when viewed from above.
- Answer
- \(\displaystyle \oint \vecs F \cdot dS = -4\)
29. Use the surface integral in Stokes’ theorem to calculate the circulation of field \(\vecs F,\) \(\vecs F(x,y,z) = x^2y^3 \,\mathbf{\hat i} + \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) around \(C,\) which is the intersection of cylinder \(x^2 + y^2 = 4\) and hemisphere \(x^2 + y^2 + z^2 = 16, \, z \geq 0\), oriented counterclockwise when viewed from above.
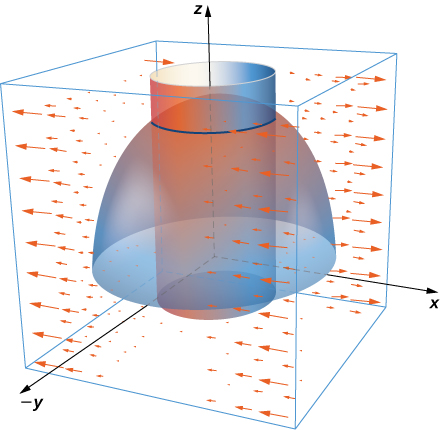
30. Use Stokes’ theorem to compute \(\displaystyle \iint_S curl \, \vecs F \cdot dS.\) where \(\vecs F(x,y,z) = \,\mathbf{\hat i} + xy^2\,\mathbf{\hat j} + xy^2 \,\mathbf{\hat k}\) and \(S\) is a part of plane \(y + z = 2\) inside cylinder \(x^2 + y^2 = 1\) and oriented counterclockwise.
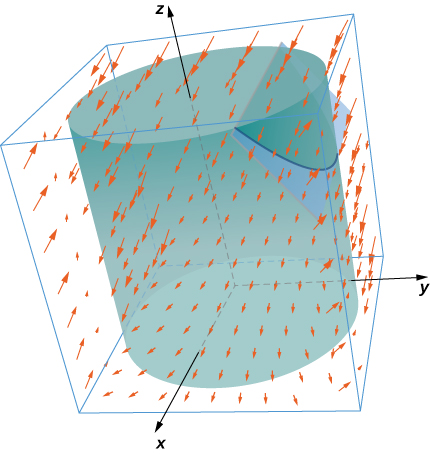
- Answer
- \(\displaystyle \iint_S curl \, \vecs F \cdot dS = 0\)
31. Use Stokes’ theorem to evaluate \(\displaystyle \iint_S curl \, \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = -y^2 \,\mathbf{\hat i} + x\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}\) and \(S\) is the part of plane \(x + y + z = 1\) in the positive octant and oriented counterclockwise \(x \geq 0, \, y \geq 0, \, z \geq 0\).
32. Let \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + 2z\,\mathbf{\hat j} - 2y\,\mathbf{\hat k}\) and let \(C\) be the intersection of plane \(x + z = 5\) and cylinder \(x^2 + y^2 = 9\), which is oriented counterclockwise when viewed from the top. Compute the line integral of \(\vecs F\) over \(C\) using Stokes’ theorem.
- Answer
- \(\displaystyle \iint_S curl \, \vecs F \cdot dS = -36 \pi\)
33. [T] Use a CAS and let \(\vecs F(x,y,z) = xy^2\,\mathbf{\hat i} + (yz - x)\,\mathbf{\hat j} + e^{yxz}\,\mathbf{\hat k}\). Use Stokes’ theorem to compute the surface integral of curl \(\vecs F\) over surface \(S\) with inward orientation consisting of cube \([0,1] \times [0,1] \times [0,1]\) with the right side missing.
34. Let \(S\) be ellipsoid \(\dfrac{x^2}{4} + \dfrac{y^2}{9} + z^2 = 1\) oriented counterclockwise and let \(\vecs F\) be a vector field with component functions that have continuous partial derivatives.
- Answer
- \(\displaystyle \iint_S curl \, \vecs F \cdot \vecs N = 0\)
35. Let \(S\) be the part of paraboloid \(z = 9 - x^2 - y^2\) with \(z \geq 0\). Verify Stokes’ theorem for vector field \(\vecs F(x,y,z) = 3z\,\mathbf{\hat i} + 4x\,\mathbf{\hat j} + 2y\,\mathbf{\hat k}\).
36. [T] Use a CAS and Stokes’ theorem to evaluate \(\displaystyle \oint \vecs F \cdot dS,\) if \(\vecs F(x,y,z) = (3z - \sin x) \,\mathbf{\hat i} + (x^2 + e^y) \,\mathbf{\hat j} + (y^3 - \cos z) \,\mathbf{\hat k}\), where \(C\) is the curve given by \(x = \cos t, \, y = \sin t, \, z = 1; \, 0 \leq t \leq 2\pi\).
- Answer
- \(\displaystyle \oint_C \vecs F \cdot d\vecs{r} = 0\)
37. [T] Use a CAS and Stokes’ theorem to evaluate \(\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + e^z\,\mathbf{\hat j} - \arctan x \,\mathbf{\hat k}\) with \(S\) as a portion of paraboloid \(z = 4 - x^2 - y^2\) cut off by the \(xy\)-plane oriented counterclockwise.
38. [T] Use a CAS to evaluate \(\displaystyle \iint_S curl (F) \cdot dS,\) where \(\vecs F(x,y,z) = 2z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 5y\,\mathbf{\hat k}\) and \(S\) is the surface parametrically by \(\vecs r(r,\theta) = r \, \cos \theta \,\mathbf{\hat i} + r \, \sin \theta \,\mathbf{\hat j} + (4 - r^2) \,\mathbf{\hat k} \, (0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 3)\).
- Answer
- \(\displaystyle \iint_S curl (F) \cdot dS = 84.8230\)
39. Let \(S\) be paraboloid \(z = a (1 - x^2 - y^2)\), for \(z \geq 0\), where \(a > 0\) is a real number. Let \(\vecs F(x,y,z) = \langle x - y, \, y + z, \, z - x \rangle\). For what value(s) of \(a\) (if any) does \(\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS\) have its maximum value?
For application exercises 40 - 41, the goal is to evaluate \(\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS,\) where \(\vecs F = \langle xz, \, -xz, \, xy \rangle\) and \(S\) is the upper half of ellipsoid \(x^2 + y^2 + 8z^2 = 1\), where \(z \geq 0\).
40. Evaluate a surface integral over a more convenient surface to find the value of \(A.\)
- Answer
- \(\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS = 0\)
41. Evaluate \(A\) using a line integral.
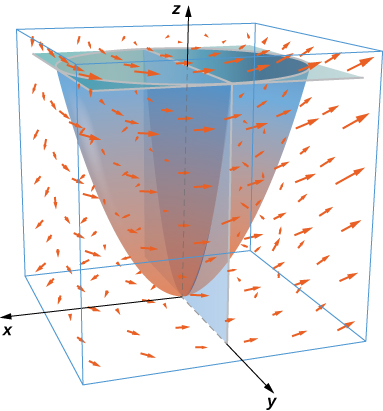
42. Take paraboloid \(z = x^2 + y^2\), for \(0 \leq z \leq 4\), and slice it with plane \(y = 0\). Let \(S\) be the surface that remains for \(y \geq 0\), including the planar surface in the \(xz\)-plane. Let \(C\) be the semicircle and line segment that bounded the cap of \(S\) in plane \(z = 4\) with counterclockwise orientation. Let \(\vecs F = \langle 2z + y, \, 2x + z, \, 2y + x \rangle\). Evaluate \(\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS.\)
- Answer
- \(\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS = 2\pi\)
For exercises 43 - 45, let \(S\) be the disk enclosed by curve \(C \, : \, \vecs r(t) = \langle \cos \varphi \, \cos t, \, \sin t, \, \sin \varphi \, \cos t \rangle\), for \(0 \leq t \leq 2\pi\), where \(0 \leq \varphi \leq \dfrac{\pi}{2}\) is a fixed angle.
43. What is the length of \(C\) in terms of \(\varphi\)?
44. What is the circulation of \(C\) of vector field \(\vecs F = \langle -y, \, -z, \, x \rangle\) as a function of \(\varphi\)?
- Answer
- \(C = \pi (\cos \varphi - \sin \varphi)\)
45. For what value of \(\varphi\) is the circulation a maximum?
46. Circle \(C\) in plane \(x + y + z = 8\) has radius \(4\) and center \((2, 3, 3).\) Evaluate \(\displaystyle \oint_C \vecs F \cdot d\vecs{r}\) for \(\vecs F = \langle 0, \, -z, \, 2y \rangle\), where \(C\) has a counterclockwise orientation when viewed from above.
- Answer
- \(\displaystyle \oint_C \vecs F \cdot d\vecs{r} = 48 \pi\)
47. Velocity field \(v = \langle 0, \, 1 -x^2, \, 0 \rangle \), for \(|x| \leq 1\) and \(|z| \leq 1\), represents a horizontal flow in the \(y\)-direction. Compute the curl of \(\vecs v\) in a clockwise rotation.
48. Evaluate integral \(\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS,\) where \(\vecs F = - xz\,\mathbf{\hat i} + yz\,\mathbf{\hat j} + xye^z \,\mathbf{\hat k}\) and \(S\) is the cap of paraboloid \(z = 5 - x^2 - y^2\) above plane \(z = 3\), and \(\vecs n\) points in the positive \(z\)-direction on \(S.\)
- Answer
- \(\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n = 0\)
In exercises 49 - 50, use Stokes’ theorem to find the circulation of the following vector fields around any smooth, simple closed curve \(C.\)
49. \(\vecs F = \vecs \nabla (x \, \sin ye^z)\)
50. \(\vecs F = \langle y^2z^3, \, z2xyz^3, 3xy^2z^2 \rangle \)
- Answer
- \(0\)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


