2.15: Homework- Examples of the Definition of the Derivative
- Page ID
- 88639
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Simplify each expression involving fractions or rational expressions.
- \((x+1) \cdot \left( \frac{1}{3} + \frac{x}{x+1} \right)\)
\(=\frac{x+1}{3} + x = \frac{4x+1}{3}\)ans
- \(\cfrac{\cfrac{1}{3} + 1}{1-\cfrac{1}{3}}\)
\(2\)ans
- \(\cfrac{x + 1}{\cfrac{1}{x}}\)
\(x^2 + x\)ans
- \(\cfrac{\cfrac{1}{x} - \cfrac{1}{x+1}}{\cfrac{1}{x} + \cfrac{1}{x+1}}\)
\(\frac{1}{2x+1}\)ans
- \(\cfrac{\cfrac{2}{x} - \cfrac{1}{x}}{\cfrac{1 - y}{y}}\)
\(\frac{y}{x - xy}\)ans
- \((x+1) \cdot \left( \frac{1}{3} + \frac{x}{x+1} \right)\)
- In each case, use the definition of the derivative to find \(f'(x)\) (in other words, take the derivative!)
- \(f(x) = 3x - 5 \)
\(3\)ans
- \(f(x) = \frac{1}{2} x + 1 \)
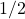ans - \(f(x) = 2 x^2\)
\(4x\)ans
- \(f(x) = (x^2 + x)\)
\(2x + 1\)ans
- \(\frac{d}{dx} (e^x)\) (hint: from yesterday’s homework, we have \(\lim_{h \to 0} \frac{e^h - 1}{h} = 1\))
\(e^x\)ans
- \(f(x) = x^3\)
\(x^3\)ans
- \(f(x) = 3x - 5 \)
- In each case, use the definition of the derivative to find \(f'(x)\) (in other words, take the derivative!). Each of these is like one of the “hard problems” (click here)
- \(f(x) = 2x^4\)
\(8x^3\)ans
- \(f(x) = \sqrt{2x}\)
\(\frac{1}{\sqrt{2x}}\)ans
- \(f(x) = \frac{2}{x} \)
\(-\frac{2}{x^2}\)ans
- \(f(x) = \sqrt{x+1}\)
\(\frac{1}{2 \sqrt{x+1}}\)ans
- \(f(x) = \frac{1}{x+1} \)
\(-\frac{1}{(x+1)^2}\)ans
- \(f(x) = \frac{1}{\sqrt{x}}\)
\(\frac{-1}{2 x \sqrt{x}}\)ans
- \(f(x) = 2x^4\)
- Recall the derivative of \(f(x) = x^2\) is given by \(2x\).
- Show that the derivative of \(g(x) = x^2+1\) is \(2x\) using the definition of the derivative. Can you find an intuitive reason why \(f(x)\) and \(g(x)\) would have the same derivative?
Adding a constant moves the curve up or down, but that shift does not affect the slope of the tangent lineans
- Find another function whose derivative is \(2x\), other than \(f(x)\) and \(g(x)\).
\(x^2 + c\) for any value \(c\)ans
- Show that the derivative of \(g(x) = x^2+1\) is \(2x\) using the definition of the derivative. Can you find an intuitive reason why \(f(x)\) and \(g(x)\) would have the same derivative?