4.8: Homework- Derivatives in Space

Last updated
Save as PDF

Page ID: 88664

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

We’ve talked a lot about how derivatives measure slope, but literal slope on a topographic map is a good example of derivatives in space. Consider this picture:
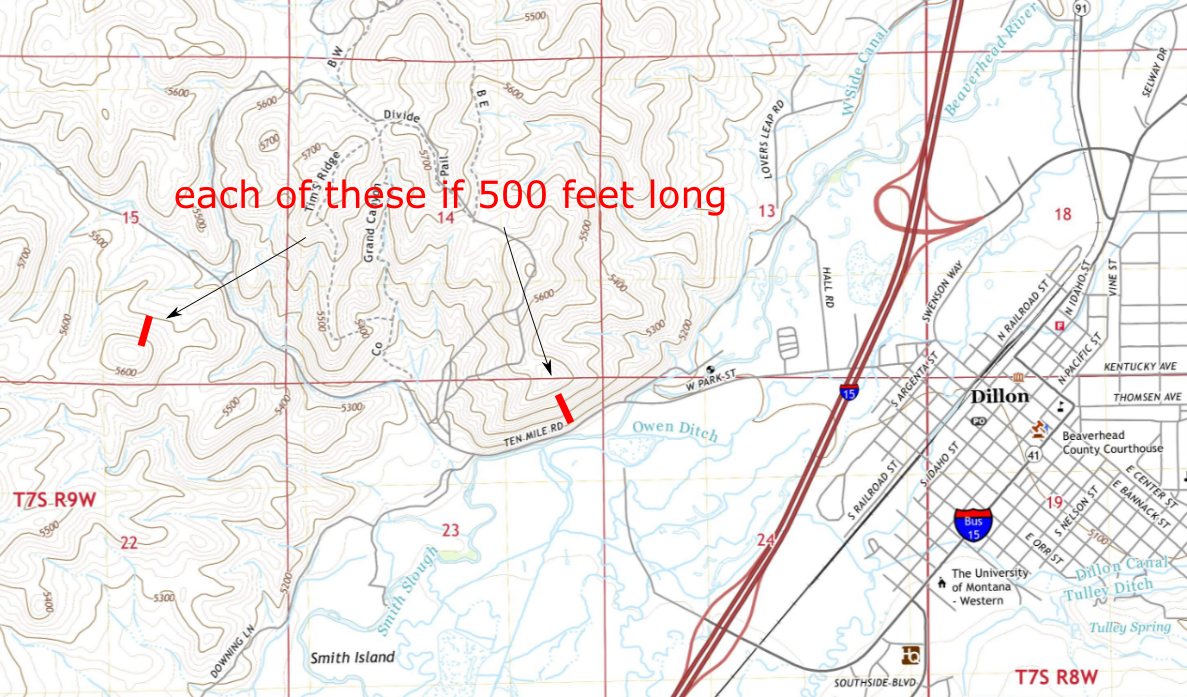
$geo-map-dillon.png$

src: usgs.gov’s topoview

The thinnest contours on the map represent a height gain of $20$ feet, and the slightly thicker contours are a height gain of $100$ feet. Each thick red line has a length of roughly $500$ feet. What is the slope of the mountain at the thick red lines?
Consider the following thermal image of wolves howling:
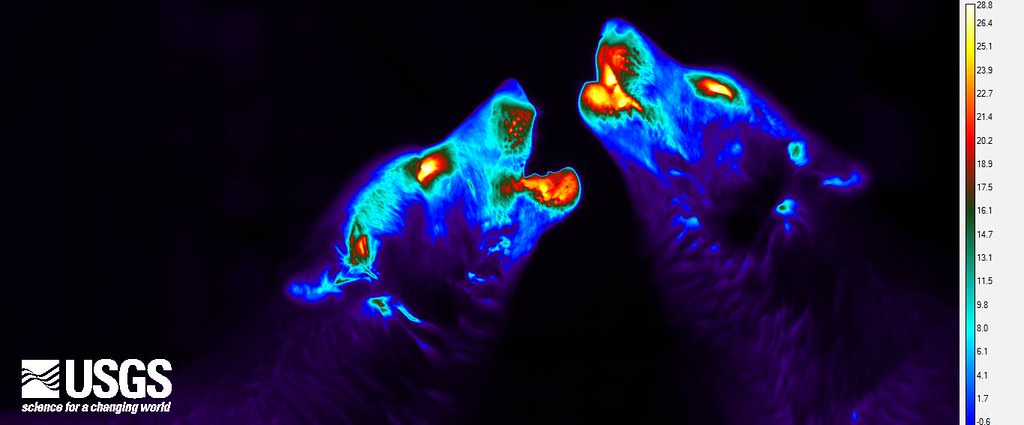
$Thermal image of wolves howling. Their eyes and mouths show higher temperatures than their fur.$

src: usgs.gov
1. Why is the eyes and mouth much hotter than other parts of the wolves, like the neck?
2. According to the heat equation, things get colder or warmer depending on the second derivative with respect to space. Assuming these wolves are a constant temperature, that means the second derivative of temperature with respect to space is zero. What does it mean for the first derivative if the second derivative is zero? What does that mean for the temperature of the wolves at different places on its body where the fur is thinner or thicker?
Consider a cylinder filled with particles of some important nutrient (say oxygen). Suppose the concentration isn’t constant, but instead looks something like this:
$diffusion.svgfixme$

The oxygen particles will tend to move from areas of high concentration to areas of low concentration, a process called diffusion. Diffusion is extremely important in biology, since that is how many cells get their nutrients.
1. Based on the diagram of the cylinder, draw a rough sketch of the concentration graph. On the $y$-axis should be concentration $C$ (molecules per cm$^3$), and on the $x$-axis should be distance $x$ from the back of the cylinder measured in cm.
2. Based on your graph, estimate the slope at two points of your choosing. The notation for your answers would be $\frac{dC}{dx}$.
3. The rate at which the particles move in diffusion is called flux. It follows Fick’s law:
  $\text{Flux} = -D \cdot \frac{dC}{dx}$
  
  Here, flux is how fast the particles are moving, $D$ is the diffusion coefficient (a constant), and $\frac{dC}{dx}$ is what we found in the previous part. Why is there a negative in the equation? Explain it in words, and talk about your graph and your answers for $\frac{dC}{dx}$ from the previous part.