5.6: Homework- Understanding Differential Equations

Last updated
Save as PDF

Page ID: 88670

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

For each differential equation below, do the following steps.
- Describe what each variable or function is measuring (if possible at this stage), and give correct units.
- Describe what the equation is saying. Use phrasing like “If such-and-such is big, than such-and-such grows faster.”
- Explain why the relationships from the previous bullet point makes sense in terms of the story or physical situation.
1. Let $T(t)$ be the temperature of a cooling object in degrees Celsius, and let $t$ be measured in seconds. Newton’s law of cooling state that $T'(t) = -k(T(t) - T_{\text{air}})$. Here $T_{\text{air}}$ is the ambient air temperature.
2. Let $H(t)$ be the height of a mountain measured in meters over a long period of time ($t$ measured in millions of years). Suppose $H(t)$ satisfies the differential equation $quicklatex.com-b22088a61553e94774ad470a0ae230b0_l3.png$ .
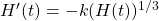3. Let $y(t)$ be the fish population in a lake being harvested at rate $H$ fish per year. Suppose $y(t)$ satisfies the differential equation
  $y'(t) = k y(t) - (m + c y(t)) y(t) - H$. Here, $k y(t)$ represents the birth rate, $(m + cy(t)) y(t)$ the natural death rate, and $H$ the harvest rate.
Skim through the article “Campus drinking: an epidemiological model” by J. L. Manthey, A. Y. Aidoo & K. Y. Ward. You’re not going to understand the whole article — that’s okay! But let’s try to figure out bits and pieces of it.
Here is their first differential equation from secion 2 of the article.

\[\[\frac{dN}{dt} = \eta - \eta N - \alpha N P + \beta S + \epsilon P\]\]
1. What does the variables N, S, and P represent?
2. In the first differential equation, what terms represent college students transitioning to drinking more? Which one represent college students transitioning to drinking less?
3. What is a main conclusion of the article?