7.1: Power, exponential, trig, and logarithm rules

Last updated
Save as PDF

Page ID: 88684

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

We’ve already seen the inverse power rule, but here it is again:

$\boxed{\int x^mdx = \frac{x^{m + 1}}{m+1} + C}$

Note that this only works if $m \neq -1$. However, we haven’t seen how this works with fractional and negative powers yet. We’ll do some examples of this.

We can also “undo” the derivatives for exponential, logarithmic functions, or trigonometric functions.

$\boxed{\int e^xdx = e^x + C}$

$\boxed{\int \frac{1}{x}dx = \ln(x) + C}$

$\boxed{\int \sin(x)dx = -\cos(x) + C}$

$\boxed{\int \cos(x)dx = \sin(x) + C}$

On to the examples. Recall that $x^{-m} = \frac{1}{x^m}$ and .

Power rule with fractional and negative powers

Find $quicklatex.com-9adff5d5f4ba8e112eb7c04e52d34ef0_l3.png$ .

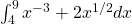Negative and fractional powers work the same way as the positive powers we’ve been working with. We see

At this point, let’s just type it into a calculator to get an approximate answer. We see that the integral is about $\boxed{23.36}$.
Find $\int_1^2 \frac{1}{x^4}dx$.

This problem becomes an inverse power rule problem if we notice that $\frac{1}{x^4} = x^{-4}$. We see

\[\begin{align*} \int_1^2 \frac{1}{x^4}dx & = \int_1^2 x^{-4}dx \\ & = \frac{x^{-5}}{-5} \Big|_1^2 \\ & = -\frac{1}{5x^5} \Big|_1^2 \\ & = \left( -\frac{1}{5(2)^5} \right) - \left( -\frac{1}{5(1)^5} \right) \\ & = -\frac{1}{160} + \frac{1}{5} \\ & = -\frac{1}{160} + \frac{32}{160} \\ & = \boxed{\frac{31}{160}}. \end{align*}\]
Find $\int_{25}^{100} \sqrt{x}dx$.

If we remember that , this is a power rule problem.

Now for logarithmic and exponential functions.

Logarithmic and Exponential functions and integration

Find $\int_1^5 \frac{2}{x}dx$.

For this problem, you may be tempted to write this as $2x^{-1}$ and use the inverse power rule. Good instincts, but in this case it won’t work (try it: it leads to division by zero!). So instead, let’s invert the natural logarithm derivative.

*** QuickLaTeX cannot compile formula:
\begin{align*}
\int_1^5 \frac{2}{x}dx & = 2 \int_1^5 \frac{1}{x}dx \\
& = 2 \left( \ln(x) \right) \Big|_1^5 \\
& = (2 \ln(5)) - (2 \ln(1)) \\
& = 2 \ln(5) - 0 \\
& = 2 \ln(5) \approx \boxed{3.2}.
\end{align*}

*** Error message:
Error: get_image_size(): -1

Find $\int_{-2}^2 7 e^{x}dx$.

$e^x$ is the best function for calculus. Doesn’t change with integration!

\[\begin{align*} \int_{-2}^2 7 e^xdx & = 7 \int_{-2}^2 e^xdx \\ & = 7 (e^x) \Big|_{-2}^2 \\ & = (7 e^{2}) - (7 e^{-2}) \end{align*}\]

Not a lot to do to simplify this, but we can get a decimal approximation: $\approx \boxed{50.78}$.