16.1: Vector Fields
- Page ID
- 4555
We have already seen that a convenient way to describe a line in three dimensions is to provide a vector that "points to'' every point on the line as a parameter \(t\) varies, like
\[\langle 1,2,3\rangle+t\langle 1,-2,2\rangle
=\langle 1+t,2-2t,3+2t\rangle.\]
Except that this gives a particularly simple geometric object, there is nothing special about the individual functions of \(t\) that make up the coordinates of this vector---any vector with a parameter, like \(\langle f(t),g(t),h(t)\rangle\), will describe some curve in three dimensions as \(t\) varies through all possible values.
Example 13.1.1
Describe the curves \(\langle \cos t,\sin t,0\rangle\), \(\langle \cos t,\sin t,t\rangle\), and \(\langle \cos t,\sin t,2t\rangle\).
Solution
As \(t\) varies, the first two coordinates in all three functions trace out the points on the unit circle, starting with \((1,0)\) when \(t=0\) and proceeding counter-clockwise around the circle as \(t\) increases. In the first case, the \(z\) coordinate is always 0, so this describes precisely the unit circle in the \(x\)-\(y\) plane. In the second case, the \(x\) and \(y\) coordinates still describe a circle, but now the \(z\) coordinate varies, so that the height of the curve matches the value of \(t\). When \(t=\pi\), for example, the resulting vector is \(\langle -1,0,\pi\rangle\). A bit of thought should convince you that the result is a helix. In the third vector, the \(z\) coordinate varies twice as fast as the parameter \(t\), so we get a stretched out helix. Both are shown in figure 13.1.1. On the left is the first helix, shown for \(t\) between 0 and \(4\pi\); on the right is the second helix, shown for \(t\) between 0 and \(2\pi\). Both start and end at the same point, but the first helix takes two full "turns'' to get there, because its \(z\) coordinate grows more slowly.
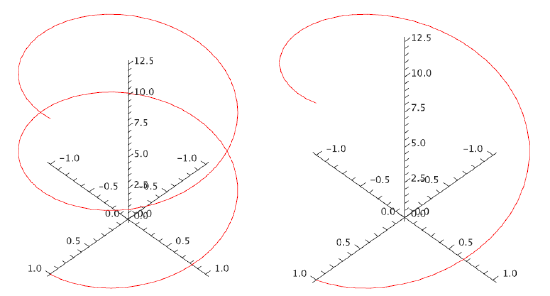
Figure 13.1.1. Two helixes.
A vector expression of the form \(\langle f(t),g(t),h(t)\rangle\) is called a vector function; it is a function from the real numbers \(\mathbb{R}\) to the set of all three-dimensional vectors.
We can alternately think of it as three separate functions, \(x=f(t)\), \(y=g(t)\), and \(z=h(t)\), that describe points in space. In this case we usually refer to the set of equations as parametric equations for the curve, just as for a line. While the parameter \(t\) in a vector function might represent any one of a number of physical quantities, or be simply a "pure number'', it is often convenient and useful to think of \(t\) as representing time. The vector function then tells you where in space
a particular object is at any time.
Vector functions can be difficult to understand, that is, difficult to picture. When available, computer software can be very helpful. When working by hand, one useful approach is to consider the "projections'' of the curve onto the three standard coordinate planes. We have already done this in part: in example 13.1.1 we noted that all three curves project to a circle in the \(x\)-\(y\) plane, since \(\langle \cos t,\sin t\rangle\) is a two dimensional vector function for the unit circle.
Example 13.1.2
Graph the projections of \(\langle \cos t,\sin t,2t\rangle\) onto the \(x\)-\(z\) plane and the \(y\)-\(z\) plane.
Solution
The two dimensional vector function for the projection onto the \(x\)-\(z\) plane is \(\langle \cos t, 2t\rangle\), or in parametric form, \(x=\cos t\), \(z=2t\). By eliminating \(t\) we get the equation \(x=\cos(z/2)\), the familiar curve shown on the left in figure~\xrefn{fig:helix projections}. For the projection onto the \(y\)-\(z\) plane, we start with the vector function \(\langle \sin t, 2t\rangle\), which is the same as \(y=\sin t\), \(z=2t\). Eliminating \(t\) gives \(y=\sin(z/2)\), as shown on the right in figure 13.1.2.
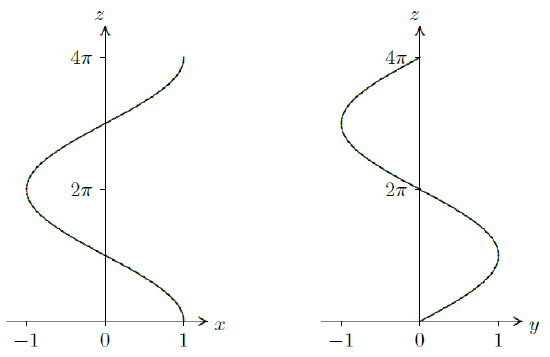
Figure 13.1.2. The projections of \(\langle \cos t,\sin
t,2t\rangle\) onto the \(x\)-\(z\) and \(y\)-\(z\) planes.

