16.4: Green's Theorem
- Page ID
- 4558
We will now see a way of evaluating the line integral of a smooth vector field around a simple closed curve. A vector field \(\textbf{f}(x, y) = P(x, y)\textbf{i} + Q(x, y)\textbf{j}\) is smooth if its component functions \(P(x, y)\) and \(Q(x, y)\) are smooth. We will use Green’s Theorem (sometimes called Green’s Theorem in the plane) to relate the line integral around a closed curve with a double integral over the region inside the curve:
Theorem 4.7: Green's Theorem
Let \(R\) be a region in \(\mathbb{R}^2\) whose boundary is a simple closed curve \(C\) which is piecewise smooth. Let \(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\) be a smooth vector field defined on both \(R\) and \(C\). Then
\[\oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P}{ ∂y} \right )\,dA, \label{Eq4.21}\]
where \(C\) is traversed so that \(R\) is always on the left side of \(C\).
Proof: We will prove the theorem in the case for a simple region \(R\), that is, where the boundary curve \(C\) can be written as \(C = C_1 \cup C_2\) in two distinct ways:
\[\begin{align} C_1 &= \text{ the curve }y = y_1(x)\text{ from the point }X_1 \text{ to the point }X_2 \label{Eq4.22} \\[4pt] C_2 &=\text{ the curve }y = y_2(x) \text{ from the point }X_2 \text{ to the point } X_1 , \label{Eq4.23} \\[4pt] \end{align}\]
where \(X_1\) and \(X_2\) are the points on \(C\) farthest to the left and right, respectively; and
\[\begin{align} C_1 &= \text{ the curve }x = x_1(y)\text{ from the point }Y_2 \text{ to the point } Y_1 \label{Eq4.24} \\[4pt] C_2 &= \text{ the curve } x = x_2(y)\text{ from the point } Y_1 \text{ to the point }Y_2,\label{Eq4.25} \\[4pt] \end{align}\]
where \(Y_1\) and \(Y_2\) are the lowest and highest points, respectively, on \(C\). See Figure 4.3.1.
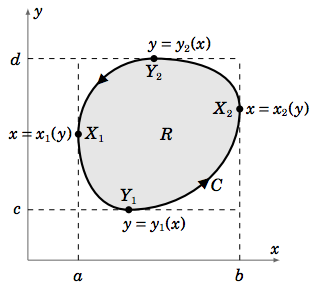
Integrate \(P(x, y)\) around \(C\) using the representation \(C = C_1 \cup C_2\) given by Equation \ref{Eq4.23} and Equation \ref{Eq4.24}.
Since \(y = y_1(x) \text{ along }C_1\) (as \(x\) goes from \(a \text{ to }b)\) and \(y = y_2(x) \text{ along }C_2\) (as \(x\) goes from \(b \text{ to }a)\), as we see from Figure 4.3.1, then we have
\[\nonumber \begin{align} \oint_C P(x, y)\,dx&=\int_{C_1}P(x, y)\,dx+\int_{C_2}P(x, y)\,dx \\[4pt] \nonumber &=\int_a^b P(x, y_1(x))\,dx+\int_b^a P(x, y_2(x))\,dx \\[4pt] \nonumber &=\int_a^b P(x, y_1(x))\,dx - \int_a^b P(x, y_2(x))\,dx \\[4pt] \nonumber &=-\int_a^b (P(x, y_2(x)) - P(x, y_1(x)))\, dx \\[4pt] \nonumber &=-\int_a^b \left ( P(x, y) \Big |_{y=y_1(x)}^{y=y_2(x)} \right )\,dx \\[4pt] \nonumber &=-\int_a^b \int_{y_1(x)}^{y_2(x)} \dfrac{∂P(x, y)}{ ∂y}\,dy\,dx \text{ (by the Fundamental Theorem of Calculus)} \\[4pt] &=-\iint\limits_R \dfrac{∂P}{ ∂y}\,dA. \\[4pt] \label{Eq4.26} \end{align}\]
Likewise, integrate \(Q(x, y)\) around \(C\) using the representation \(C = C_1 \cup C_2\) given by Equation \ref{Eq4.25} and Equation \ref{Eq4.26}. Since \(x = x_1(y) \text{ along }C_1\) (as \(y\) goes from \(d\) to \(c\)) and \(x = x_2(y) \text{ along }C_2\) (as \(y\) goes from \(c\) to \(d\)), as we see from Figure 4.3.1, then we have
\[\nonumber \begin{align} \oint_C Q(x, y)\,dy&=\int_{C_1}Q(x, y)\,dy+\int_{C_2}Q(x, y)\,dy \\[4pt] \nonumber &=\int_d^c Q(x_1(y), y)\,dy+\int_c^d Q(x_2(y), y)\,dy \\[4pt] \nonumber &=-\int_c^d Q(x_1(y), y)\,dy + \int_c^d Q(x_2(y), y)\,dy \\[4pt] \nonumber &=\int_c^d (Q(x_2(y), y) - Q(x_1(y), y))\, dy \\[4pt] \nonumber &=\int_c^d \left ( Q(x, y) \Big |_{x=x_1(y)}^{x=x_2(y)} \right )\,dy \\[4pt] \nonumber &=\int_c^d \int_{x_1(y)}^{x_2(y)} \dfrac{∂Q(x, y)}{ ∂x}\,dx\,dy \text{ (by the Fundamental Theorem of Calculus)} \\[4pt] \nonumber &=\iint\limits_R \dfrac{∂Q}{ ∂x}\,dA,\text{ and so} \\[4pt] \end{align}\]
\[\nonumber \begin{align} \oint_C \textbf{f}\cdot d\textbf{r} &= \oint_C P(x, y)\,dx + \oint_C Q(x, y)\,d y \\[4pt] \nonumber &= -\iint_R \dfrac{∂P}{ ∂y}\,dA + \iint_R \dfrac{∂Q}{∂x}\,dA \\[4pt] \nonumber &= \iint_R \left ( \dfrac{∂Q}{ ∂x}-\dfrac{∂P}{ ∂y} \right ) \,dA. \\[4pt] \end{align}\]
\(\tag{\(\textbf{QED}\)}\)
Though we proved Green’s Theorem only for a simple region \(R\), the theorem can also be proved for more general regions (say, a union of simple regions).
Example 4.7
Evaluate \(\oint_C (x^2 + y^2 )\,dx+2x y\, d y\), where \(C\) is the boundary (traversed counterclockwise) of the region \(R = {(x, y) : 0 ≤ x ≤ 1, 2x^2 ≤ y ≤ 2x}\).
\(R\) is the shaded region in Figure 4.3.2. By Green’s Theorem, for \(P(x, y) = x^2 + y^2 \text{ and }Q(x, y) = 2x y\), we have
\[\nonumber \begin{align} \oint_C (x^2+y^2)\,dx+2x y \,d y &=\iint_R \left ( \dfrac{∂Q}{ ∂x}-\dfrac{∂P}{ ∂y} \right ) \, dA \\[4pt] \nonumber &=\iint_R (2y−2y)\,d A = \iint_R 0\,dA = 0. \\[4pt] \end{align}\]
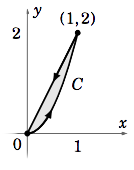
We actually already knew that the answer was zero. Recall from Example 4.5 in Section 4.2 that the vector field \(\textbf{f}(x, y) = (x^2 + y^2 )\textbf{i}+2x y\textbf{j}\) has a potential function \(F(x, y) = \dfrac{1}{3} x^3 + x y^2\), and so \(\oint_C \textbf{f}\cdot d\textbf{r} = 0\) by Corollary 4.6.
Example 4.8
Let \(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\), where
\[\nonumber P(x, y) =\dfrac{-y}{x^2+y^2} \text{ and }Q(x, y) =\dfrac{x}{x^2+y^2},\]
and let \(R = {(x, y) : 0 < x^2 + y^2 ≤ 1}\). For the boundary curve \(C : x^2 + y^2 = 1\), traversed counterclockwise, it was shown in Exercise 9(b) in Section 4.2 that \(\oint_C \textbf{f}\cdot d\textbf{r} = 2π\). But
\[\nonumber \dfrac{∂Q }{∂x} = \dfrac{y^2+x^2}{(x^2+y^2)^2} = \dfrac{∂P }{∂y} \Rightarrow \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{ ∂P}{ ∂y} \right )\,dA= \iint\limits_R 0\,dA = 0\]
This would seem to contradict Green’s Theorem. However, note that \(R\) is not the entire region enclosed by \(C\), since the point \((0,0)\) is not contained in \(R\). That is, \(R\) has a “hole” at the origin, so Green’s Theorem does not apply.
If we modify the region \(R\) to be the annulus \(R = {(x, y) : 1/4 ≤ x^2 + y^2 ≤ 1}\) (see Figure 4.3.3), and take the “boundary” \(C \text{ of }R \text{ to be }C = C_1 \cup C_2\), where \(C_1\) is the unit circle \(x^2 + y^2 = 1\) traversed counterclockwise and \(C_2\) is the circle \(x^2 + y^2 = 1/4\) traversed clockwise, then it can be shown (see Exercise 8) that
\[\nonumber \oint_C \textbf{f} \cdot d\textbf{r} = 0 \]
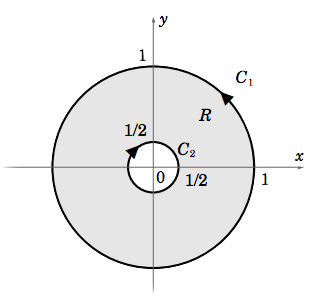
We would still have \(\iint\limits_R \left ( \dfrac{∂Q}{∂x} − \dfrac{∂P}{ ∂y } \right )\,d A = 0\), so for this \(R\) we would have
\[\nonumber \oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P}{ ∂y} \right ) \, dA,\]
which shows that Green’s Theorem holds for the annular region \(R\).
It turns out that Green’s Theorem can be extended to multiply connected regions, that is, regions like the annulus in Example 4.8, which have one or more regions cut out from the interior, as opposed to discrete points being cut out. For such regions, the “outer” boundary and the “inner” boundaries are traversed so that \(R\) is always on the left side.
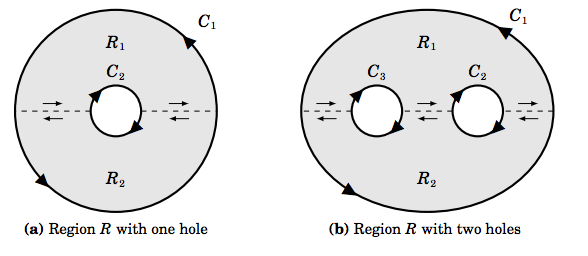
The intuitive idea for why Green’s Theorem holds for multiply connected regions is shown in Figure 4.3.4 above. The idea is to cut “slits” between the boundaries of a multiply connected region \(R\) so that \(R\) is divided into subregions which do not have any “holes”. For example, in Figure 4.3.4(a) the region \(R\) is the union of the regions \(R_1 \text{ and }R_2\), which are divided by the slits indicated by the dashed lines. Those slits are part of the boundary of both \(R_1 \text{ and }R_2\), and we traverse then in the manner indicated by the arrows. Notice that along each slit the boundary of \(R_1\) is traversed in the opposite direction as that of \(R_2\), which means that the line integrals of \textbf{f} along those slits cancel each other out. Since \(R_1 \text{ and }R_2\) do not have holes in them, then Green’s Theorem holds in each subregion, so that
\[\nonumber \oint_{bdy\,of\,R_1}\textbf{f} \cdot d\textbf{r} = \iint\limits_{R_1}\left (\dfrac{ ∂Q }{∂x} - \dfrac{∂P }{∂y} \right )\,dA \text{ and }\oint_{bdy\,of\,R_2}\textbf{f}\cdot d\textbf{r} = \iint\limits{R_2} \left ( \dfrac{∂Q }{∂x} - \dfrac{∂P}{ ∂y} \right )\,dA.\]
But since the line integrals along the slits cancel out, we have
\[\nonumber \oint_{C_1 \cup C_2} \textbf{f}\cdot d\textbf{r} = \oint_{bdy\,of\,R_1} \textbf{f} \cdot d\textbf{r} +\oint_{bdy\,of\,R_2}\textbf{f}\cdot d\textbf{r},\]
and so
\[\nonumber \oint_{C_1 \cup C_2} \textbf{f}\cdot d\textbf{r} = \iint\limits_{R_1} \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \,dA + \iint\limits_{R_2} \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \,dA = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P }{∂y} \right ) \,dA,\]
which shows that Green’s Theorem holds in the region \(R\). A similar argument shows that the theorem holds in the region with two holes shown in Figure 4.3.4(b).
We know from Corollary 4.6 that when a smooth vector field \(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\) on a region \(R\) (whose boundary is a piecewise smooth, simple closed curve \(C\)) has a potential in \(R\), then \(\oint_C \textbf{f}\cdot d\textbf{r} = 0\). And if the potential \(F(x, y)\) is smooth in \(R\), then \(\dfrac{∂F}{ ∂x} = P \text{ and }\dfrac{∂F}{ ∂y} = Q\), and so we know that
\[\nonumber \dfrac{∂^2F }{∂y∂x} = \dfrac{∂^2F}{ ∂x∂y} \Rightarrow \dfrac{∂P}{ ∂y} = \dfrac{∂Q }{∂x}\text{ in }R\]
Conversely, if \(\dfrac{∂P}{ ∂y} = \dfrac{∂Q}{ ∂x}\) in \(R\) then
\[\nonumber \oint_C \textbf{f} \cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q }{∂x}-\dfrac{∂P }{∂y} \right ) \,dA \iint\limits_R 0\,dA = 0 \]
For a simply connected region \(R\)(i.e. a region with no holes), the following can be shown:
The following statements are equivalent for a simply connected region \(R\) in \(\mathbb{R}^2\) :
- \(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j} \) has a smooth potential \(F(x, y)\) in \(R\)
- \(\int_C \textbf{f}\cdot d\textbf{r}\) is independent of the path for any curve \(C\) in \(R\)
- \(\oint_C \textbf{f} \cdot d\textbf{r} = 0\) for every simple closed curve \(C\) in \(R\)
- \(\dfrac{ ∂P}{ ∂y} = \dfrac{∂Q }{∂x} \) in \(R\) (in this case, the differential form \(P dx+Q d y\) is exact)

